 |
Перестановки с повторениями
|
|
|
|
Тема 4. Комбинаторика
Цель: овладеть навыками подсчета количества различных комбинаций, подчиненных тем или иным условиям.
Задание:
1. изучить материал данной лекции;
2. сделать краткий конспект, который необходимо представить к зачету;
3. подготовиться к письменному опросу по данной теме;
4. подготовиться к контрольной работе по данной теме.
Общие теоретические сведения
Комбинаторика (комбинаторный анализ) - раздел дискретной математики, который посвящен решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.
пример:
· сколькими способами можно выбрать 8 карт из колоды, состоящей из 54 карт,
· сколькими способами можно составить очередь, состоящей из 15 человек
· сколькими способами можно выбрать трех дежурных по столовой из класса, в котором 30 человек;
· сколько различных трехзначных чисел можно составить из цифр 3, 4, 5, 9,0 и др.
Каждое правило в комбинаторике предопределяет способ построения некоторой конструкции, которая состоит из элементов исходного множества и называется комбинацией. Главная цель комбинаторики состоит в подсчете количества комбинаций, которые можно составить из элементов исходного множества в соответствии с заданным правилом. Простейшими примерами комбинаторных конструкций являются перестановки, размещения и сочетания.
Появление комбинаторики связано с работами Б. Паскаля и П. Ферма по поводу азартных игр, большой вклад внесли Лейбниц, Бернулли, Эйлер. В настоящее время интерес к комбинаторике связан с развитием компьютерных технологий. Нас в комбинаторике будет интересовать возможность определения количественно различных подмножеств конечных множеств для вычисления вероятности классическим способом.
|
|
|
Важными задачами в комбинаторике являются:
1. определение вида соединения;
2. подсчет числа соединений.
Для определения мощности множества, которое соответствует тому или иному событию, полезно разобраться с двумя правилами комбинаторики: правило произведения и правило суммы (иногда их называют принципами умножения и сложения соответственно).
В теории вероятностей принято говорить не о комбинациях, а о выборках. Поэтому мы будем придерживаться термина «выборка». Мы рассмотрим виды выборок - перестановки, размещения, сочетания. Как увидим дальше, выборки могут в отличие от множеств включать повторно тот или иной элемент.
Общие правила комбинаторики
Рассмотрим два общих правила, с помощью которых решается большинство задач комбинаторики - правило суммы и правило произведения.
Правило суммы: Если, некоторый объект А можно выбрать n способами, а объект В - m способами (не такими, как А), то выбор «либо А, либо В» может быть осуществлен т + n способами.
пример: На столе лежит 7 учебников по русскому языку и 8 по математике. Сколькими способами можно выбрать один учебник?
решение: В задаче речь идет о выборе 1 элемента из 2 данных множеств: обозначим А - учебники по русскому языку, В - учебники по математике. Учебник выбираем по русскому языку или математике. Так как множества объединены с помощью союза или, значит используем правило суммы. Мощность множества А: m(A) = 7, множества В: m(В) = 8, значит учебник по русскому языку можно выбрать 7 способами, учебник по математике 8 способами. Следовательно, общее число способов 7+8 = 15. Ответ: 15 способами можно выбрать один учебник.
При применении правила суммы нужно учитывать, чтобы ни один из способов выбора объекта А не совпадал с каким-нибудь способом выбора объекта В, т.е. чтобы ни одна комбинация не попала сразу в два класса. Если все же такие совпадения имеются, правило сложения в представленной выше форме теряет свою силу, а получаем т + n - k, где k - число совпадений.
|
|
|
Общее правило суммы: Если объект А можно выбрать т способами, а объект В - n способами, причем при k способах одновременно выбираются и А, и В, то выбор "А или В" может быть осуществлен т + n - k способами.
пример: Сколько чисел в первой сотне, не делящихся ни на 2, ни на 3?
решение: Сначала вычислим количество чисел первой сотни, которые делятся на 2 или на 3.Мы знаем, что каждое второе число в натуральном ряде делится на 2, каждое третье - на 3. Значит в первой сотне будет 50 чисел, которые делятся на 2, и 33 числа (неполное частное от деления 100 на 3), делящихся на 3. Но среди первых и вторых есть числа, делящиеся и на 2, и на 3, т. е. делящиеся на 6. На 6 делится каждое шестое число в натуральном ряде. Если 100 разделить на 6, то неполное частное будет равняться 16, т. е. 16 чисел в первой сотне делится на 6. Итак, количество чисел в первой сотне, делящихся на 2 или на 3, равно 50 + 33 – 16 = 67. Все остальные не делятся ни на 2, ни на 3. Этих чисел 100 – 67 = 33.
Правило произведений: Если объект А можно выбрать т способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) n способами, то пары объектов А и В можно выбрать m × n способами.
пример: На столе лежит 7 учебников по русскому языку и 8 по математике. Сколькими способами можно выбрать пару, которая состоит из учебника по русскому языку и математике?
решение: В задаче речь идет о двух множествах: обозначим А - учебники по русскому языку, В - учебники по математике. Учебники выбираем по русскому языку и математике. Так как множества объединены с помощью союза и, значит используем правило произведения. Мощность множества А: m(A) = 7, множества В: m(В) = 8, значит учебник по русскому языку можно выбрать 7 способами, учебник по математике 8 способами. Следовательно, общее число способов выбрать пару учебников 7×8 = 56. Ответ: 56 способами можно выбрать пару учебников.
Факториал. Правила.
1. Факториалом числа n называется произведение всех натуральных чисел, меньше или равных n. Факториал обозначается n!
n!=1⋅2⋅3…(n−1)⋅n
|
|
|
2. Нужно запомнить, что факториал 0 по определению равен 1.
0!=1
1!=1
2!=1×2=2
3!=1×2×3=6
4!=1×2×3×4=24
5!= 1×2×3×4×5=120
6!= 1×2×3×4×5×6=720
7!= 1×2×3×4×5×6×7=5040
(n-1)!= 1×2×3×4×5×(n-2)×(n-1)
(n+1)!= 1×2×3×4×5×(n-2)×(n-1)×n×(n+1)
Число n может принимать не только натуральные значения, оно может также равняться нулю. Пустое множество (выборка) является подмножеством любого множества, и естественно считать, что оно может быть упорядочено только одним способом.
Соединения без повторений
| Обращают внимание на порядок раположения элементов |
| Если порядок не имеет значения, то применяем сочетание |
| Если порядок имеет значение, то применяем либо размещение, либо перестановки |
| Если не все элементы, то это - размещения |
| Если все элементы, то это - перестановки |
Рис. 1 Схема выбора вида соединения
Перестановки
Перестановки - всевозможные упорядоченные множества, которые составлены из всех элементов данного множества. Число всевозможных перестановок из n элементов, обозначают  и находят по формуле:
и находят по формуле:
 = n! = n!
|
пример: Сколькими способами можно расставить в шеренгу школьников, класса из 10 человек?
решение: Число способов, которое нам требуется найти, это и есть число перестановок, значит:  =10×9×8×7×6×5×4×3×2×1=3.628.800
=10×9×8×7×6×5×4×3×2×1=3.628.800
Смысловая нагрузка: "Сколькими способами можно переставить п объектов?"
Сочетания
Сочетаниями - из n по m называются всевозможные неупорядоченные подмножества данных n элементов, состоящие из m элементов. Для подсчета числа сочетаний используется следующее обозначение и формула:
 = =  = = 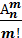
|
пример: Сколькими способами можно из 10 различных открыток выбрать 4?
решение: Четыре открытки являются неупорядоченным подмножеством 10 открыток, значит применяем формулу для сочетаний: 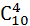 =
= 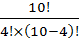 =
=  =
=  =210 способами можно из 10 открыток выбрать 4.
=210 способами можно из 10 открыток выбрать 4.
Размещения
Размещениями из n по m называются всевозможные упорядоченные подмножества, содержащие m элементов из данных n, обозначают  и находят по формуле:
и находят по формуле:
|
|
|
 =(п × (п-1) × (п-2)…(п- т+1)= =(п × (п-1) × (п-2)…(п- т+1)= 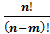
|
пример: Саша, Маша и Федор играют в карты. Сколькими способами им можно сдать по одной карте из колоды, в которой 36 карт?
решение: В данной задаче важно не только какие три карты будут извлечены из колоды, но и то. как они будут розданы игрокам. Следовательно:  = 34×35×36=42840 способами можно раздать три карты игрокам.
= 34×35×36=42840 способами можно раздать три карты игрокам.
Смысловая нагрузка: "Сколькими способами можно выбрать т объектов (из п объектов) и в каждой выборке переставить их местами?"
Исходя из определения размещений и его смысловой нагрузки, справедлива следующая формула:  ×
×  =
=  . Используем данную формулу для решения предыдущей задачи, чтобы доказать достоверность предлагаемой формулы:
. Используем данную формулу для решения предыдущей задачи, чтобы доказать достоверность предлагаемой формулы:
решение: найдем сколькими способами можно извлечь 3 карты из колоды, используем формулу сочетаний:  =
=  = 7140 способов; з карты "переставить" между игроками можно
= 7140 способов; з карты "переставить" между игроками можно  =3!=1×2×3=6 способами, следовательно, чтобы ответить на заданный вопрос требуется подставить полученные результаты в формулу:
=3!=1×2×3=6 способами, следовательно, чтобы ответить на заданный вопрос требуется подставить полученные результаты в формулу:  ×
×  =7140×6=42840 способами можно сдать по одной карте трем игрокам. В данном примере мы наглядно показали применение формулы:
=7140×6=42840 способами можно сдать по одной карте трем игрокам. В данном примере мы наглядно показали применение формулы:  ×
×  =
=  .
.
Соединения с повторениями
Не всякая выборка является множеством (и может быть поэтому подмножеством). Далее мы рассмотрим соединения (выборки) с повторениями, они множествами не являются.
Перестановки с повторениями
 = =  = = 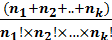
|
Смысловая нагрузка: "Количество способов. которыми можно переставить n объектов, среди которых 1-й объект повторяется n1 раз, 2-й - n2 раз, k -й объект - nk раз".
пример: Сколько различных слов можно составить, переставляя буквы в слове "математика"?
решение: Во-первых, сразу найдем повторяющиеся буквы в данном слове: "м" - 2, "а" - 3. "т" - 2, "е, и, к" - встречаются по 1 разу. Значит количество слов есть ничто иное, как количество перестановок с повторениями, следовательно -  (2, 3, 2, 1, 1, 1) =
(2, 3, 2, 1, 1, 1) =  =
=  = 151200 различных слов можно составить из слова "математика".
= 151200 различных слов можно составить из слова "математика".
Так как некоторые элементы в выборке повторяются и при их перестановке новой перестановки не получим, то понятно, что число перестановок с повторениями меньше перестановок без повторения.
Число перестановок с повторениями меньше числа перестановок без повторения во столько раз, сколько можно переставить местами одинаковые элементы.
|
|
|
Сочетание с повторениями
Дано множество n. Различные неупорядоченные наборы, составленные из m элементов этого множества так, что элементы в наборе могут повторяться, и порядок их не важен, называются сочетаниями с повторениями из n по m. Обозначаются и вычисляются по формуле:
 = =  = = 
|
Смысловая нагрузка: "Для выбора предлагается n множеств, каждое из которых состоит из одинаковых элементов. Сколькими способами можно выбрать m элементов?"
пример: "Группа из 30 студентов сдала экзамен. В отчете отражено, сколько каких оценок было получено. Сколькими способами можно составить отчет?"
решение: Требуется 30 раз выбрать из четырех оценок. По условию порядок не важен, но важно количество 2, 3, 4 и 5, которые будут повторяться. Значит, количество способов это и есть количество сочетаний с повторениями из 4 по 30, подставляем данные в формулу:  =
= 
= 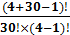 =
=  = 5456 способами может быть составлен отчет.
= 5456 способами может быть составлен отчет.
Размещение с повторениями
Различные кортежи длины m, которые составлены из элементов данного множества, содержащего n элементов, так, что эти элементы в кортеже могут повторяться, называются размещениями с повторениями из n по m. Обозначаются и вычисляются по формуле:
 = nm = nm
|
Смысловая нагрузка: "Дано множество, которое состоит из n объектов, при этом любой объект можно выбирать не один раз. Сколькими способами можно выбрать m объектов, если важен порядок их расположения в выборке?"
пример: В лифт десятиэтажного дома вошли 6 человек. Сколькими способами могут выйти люди на каждом этаже, начиная со второго?
решение: Задача сводится к распределению 6 человек по 9 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько человек могут выйти на одном этаже). Следовательно, задача сводится к нахождению числа размещений с повторениями: 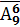 = 96 = 531441 способами люди могут выйти на каждом этаже, начиная со второго.
= 96 = 531441 способами люди могут выйти на каждом этаже, начиная со второго.
При решении комбинаторных задач в первую очередь необходимо ответить на следующие вопросы:
1. Из какого множества происходит выбор (найти n)?
2. Что требуется сделать: расставить все в ряд (перестановки P) или выбрать часть (найти m)?
3. Важен ли порядок? (важен - размещение А, не важен - С).
4. Возможны ли повторения?
Комбинаторика - изучающий задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Обобщим в схеме 1, все полученные теоретические знания.
Схема 1. Алгоритм применения комбинаторных формул.
| Выбранные m элементов нужно разместить по n различным местам (порядок имеет значение) |
| Среди выбранных элементов есть одинаковые? |
 = = 
|
| Выбранные m элементов нужно разместить по n различным местам (порядок имеет значение) |
 = = 
|
Нет Нет
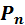 = n! = n!
|
 = =  = = 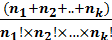
|
 = = 
|
 = nm = nm
|
| m = n да или нет? |
Да Да
| m = n да или нет? |
Нет Нет
Да Да
|
|
|


