Расчет зубчатых передач редуктора

Поля с этой стр.?

 

ВВЕДЕНИЕ

 

Производственные процессы в большинстве отраслей народного хозяй­ства выполняют машины, и дальнейший рост материального благосостояния тесно связан с развитием машиностроения.

К важнейшим требованиям, предъявляемым к проектируемой машине, относятся экономичность в изготовлении и эксплуатации, удобство и безот­казность обслуживания, надёжность и долговечность.

Для обеспечения этих требований детали должны удовлетворять ряду критериев, важнейшие среди которых – прочность, надёжность, износостой­кость, жёсткость, виброустойчивость, теплостойкость, технологичность.

Зубчатые передачи в современной промышленности имеют большое значение. Благодаря высокому КПД они широко применяются в технике. Зубчатые передачи необходимо рассчитывать на контактную и изгибную прочность, выполнить проверочный расчёт валов, подшипников, резьбовых и шлицевых соединений.

Курсовой проект по деталям машин является первой конструкторской работой студента и, поэтому её значение весьма существенно. Изучение ос­нов конструирования (проектирования) начинают с конструирования про­стейших узлов машин – приводов, редукторов. Опыт и знания, приобретен­ные студентом при конструировании этих узлов машин, являются основой для его дальнейшей конструкторской работы, а также для выполнения курсо­вых проектов по специальным дисциплинам и дипломного проекта.

 

Форматирование по ширине

 

1 Кинематический и энергетический расчет редуктора

1.1 Определение общего передаточного отношения и распределение его по ступеням

Согласно заданию имеем частоту вращения валов:
пробелы не ставятся

 

n_дв=1450 мин^-1; n_вых=310 мин^-1.

 

Общее передаточное число привода:

шрифт в формулах Times

где u_рп ‒ передаточное число ременной передачи;

u_ред ‒ передаточное число зубчатой передачи.

после точки красная строка

 

Примем u_рп = 1,65, тогда

размер шрифта в дроби

? 1.2 Определение частот вращения всех элементов привода

 

Частота вращения входного вала I:

Частота вращения выходного вала II: n₂ = n_вых = 310 .

 

? 1.3 Определение КПД ступени и мощности на валах

 

? КПД цилиндрической передачи примем η₁ = 0,98.

Мощности на валах определяются по следующей формуле:

 

? тогда:

P₂ = P_вых = 90 кВт;

? кВт.

1.4 Определение крутящих моментов на валах

 

Крутящие моменты на валах определяются по следующей формуле:

 

Ts = , тогда:

крутящий момент на валу I:

T1 = ;

 

крутящий момент на валу II:

 

T2 = .

 

точки перед-после дроби и скобки не ставятся

 

 

Расчет зубчатых передач редуктора

 

 

2.1 Выбор материала зубчатых колёс и обоснование термической обработки

Так как передача авиационная, тяжелонагруженная и требует обес­печения высокой надёжности и малых значений массогабаритных харак­теристик, то для всех зубчатых колёс выбираем высокопрочную легиро­ванную сталь 12Х2Н4А с химико-термической обработкой цементацией на глубину 1,0…1,2 мм с последующей закалкой, заготовка штамповка. Механические свойства приведены в таблице 1.

Таблица 2 – Механические свойства стали

Марка стали	Вид термо­ обработки	Механические характеристики
Твёрдость зубьев	Предел прочности σв, Мпа	Предел текучести σт, Мпа
на поверх­ности	в сердце­вине
12Х2Н4А	Цементация	HRC 58…63	HRC 35.40

2.2 Определение допускаемых контактных напряжений

Допускаемые контактные напряжения для каждого зубчатого колеса определяются по формуле

,

где σ_{H lim b} – базовый предел контактной выносливости, Мпа;

S_H – коэффициент безопасности по контактным напряжениям;

k_HL – коэффициент долговечности.

Для контакта двух цилиндров по обра­зующей принимают значение

m_H = 6.

Для стали 12Х2Н4А твёрдость поверхности составит 58…63 HRC. Принимаем HRC = 60.

Базовый предел контактной выносливости поверхности цементиро­ванных зубьев всех колёс

σ_{H lim b} = 23 HRC = 23 60 = 1380 Мпа.

Коэффициенты долговечности при расчёте по контактным напряже­ниям определяются по формуле:

 

перебрать

где N_HO – базовое число циклов перемены контактных напряжений,

Nhe – эквивалентное число циклов перемены контактных напряжений.

При большой длительности эксплуатации, когда Nhe > N_HO, вводит­ся ограничение k_HL > 1. При кратковременной работе передачи значение коэффициента долговечности также ограничивается – k_HL < 1,8 (при поверхностном упрочнении материала).

При твёрдости поверхности зубьев HRC > 56 имеем N_H0 = 12107.

Эквивалентное число циклов перемены контактных напряжений определяется по формуле:

N_Hej = 60 c_j n_j t_h,

где c_j – число нагружений зуба за один оборот j-го зубчатого колеса;

n_j – частота вращения j-го зубчатого колеса, об/мин;

t_h – долговечность, час.

Рассчитаем эквивалентное число циклов перемены контактных напряжений для зубчатых колёс 1 и 2:

Для шестерни 1:

c₁ = 1; n_j = n₁;

N_HE1 = 60 c₁ n₁ t_h = 60 1 2200 =106 339 200. 10⁷

Для зубчатого колеса 2:

c₂ = 1; n_j = n₂;

N_HE2 = 60 c₂ n₂ t_h = 60 1 310 2200 = 40 920 000.

Коэффициенты долговечности по контактным напряжениям:

;

.

Тогда допускаемые контактные напряжения будут равны:

; размерность

. размерность

В качестве расчётных допускаемых напряжений для каждой пары зубчатых колёс принимаем наименьшее значение из двух полученных:

[σ_Н ]₁₂ =1157. размерность

 

2.3 Определение допускаемых напряжений изгиба

Допускаемое напряжение изгиба для каждого зубчатого колеса определяются по формуле:

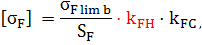
где: – базовый предел выносливости по изгибу, Мпа;

– коэффициент безопасности по напряжениям изгиба;

k_FL – коэффициент долговечности;

k_FC – коэффициент, учитывающий условия нагружения зуба.

Базовый предел выносливости по изгибу для цементированных зубьев принимаем = 800 Мпа. Паскаль

Так как поломка зуба является катастрофическим видом разруше­ния, то запасы прочности по напряжениям изгиба принимаются доста­точно большим –

S_F = 1,8.

Базовое число циклов перемены напряжений будет N_FO = 4 10⁶.

Коэффициенты долговечности при расчёте по напряжениям изгиба определяются по формуле:

,

где N_FO – базовое число циклов перемены напряжений изгиба;

N_FE – эквивалентное число циклов перемены напряжений изгиба.

При большой длительности эксплуатации, когда N_FE > _NFО, вводится ограничение k_FL > 1. При кратковременной работе передачи значение коэффициента долговечности также ограничивается ‒ k_HL < 1,63
(для закалённых передач).

Эквивалентное число циклов перемены напряжений изгиба опреде­ляется по формуле:

N_Fej = 60 c₁ n₁ t_h,

где c_j – число нагружений зуба за один оборот j-го зубчатого колеса;

n_j – частота вращения j-го зубчатого колеса, об/мин; t_h – долговечность, час.

Рассчитаем эквивалентное число циклов перемены напряжений изгиба для зубчатых колёс 1 и 2:

Для шестерни 1:

c₁ = 1; n_j = n₁;

N_FE1 = 60 c₁ n₁ t_h = 60 1 2200 = 116 000 000 точка и 10⁶

Для зубчатого колеса 2:

c₂ = 1; n_j = n₂;

N_FE2 = 60 c₂ n₂ t_h = 60 1 310 2200 = 40 920 000 точка и 10⁶

Коэффициенты долговечности по напряжениям изгиба:

 

;

.

Тогда допускаемые напряжения изгиба будут равны:

 

; Паскаль
Мпа. Паскаль

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: