Клетки матрицы заполняются в соответствии с субъективными суждениями ЛПР или группы ЛПР.

Например, при заполнении таблицы 1 на вопрос: какой критерий более важен К1 или К2, члены группы ЛПР пришли к соглашению, что К1 умеренно превосходит К2 и в соответствии со шкалой, приведенной в таблице 4.4, они внесли в клетку матрицы, стоящую на пересечении первой строки и второго столбца 3, т.е. а₁₂=3.

 

 

Таблица 3

 

Шкала относительной важности

Интенсивность относительной важности	Определение	Объяснение
2,4,6,8   Обратные величины при­веденных выше чисел	Равная важность   Умеренное превосходство одного над другим.     Существенное или сильное превосходство     Значительное превосходство     Очень сильное превосходство   Промежуточные решения между двумя соседними суждениями   Если при сравнении одного критерия с другим получено одно из вышеуказанных чисел, то при сравнении второго критерия с первым получаем обратную величину	Равный вклад двух критериев в цель. Опыт и суждения дают легкое превосходство одной альтернативы над другой Опыт и суждения дают сильное превосходство одного критерия над другим Одному из критериев дается настолько сильное предпочтение, что оно становится практически значительным Очевидность превосходства одного критерия над другим подтверждается наиболее сильно Применяется в компромиссных случаях

 

 

В симметричную относительно главной диагонали клетку, стоящую на пересечении первого столбца и второй строки, автоматически заносится 1/3, т.е.

а₂₁=1/3.

В таблице 4 эти оценки выделены жирным курсивом.

Таблица 4

Цель	К1	К2	К3
К1
К2	1/3
К3	1/7	1/3

 

Когда в решении задачи принятия решений участвуют несколько человек, по многим суждениям могут происходить споры. В таких случаях обсуждение обычно сосредоточивается на допущениях, из которых следуют суждения, а не на количественные величины самих суждений. Иногда группа принимает геометрическое среднее разных оценок в качестве общей оценки суждений

 

 

Геометрическая средняя величина дает наиболее правильный по содержанию результат, если задача состоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.

Если имеются значительные расхождения, различные мнения могут быть, сгруппированы и затем группы будут использоваться для получения ответов.

 

Те суждения в группе, в которых последовательно обнаруживается наибольшая согласованность, обычно получают всеобщую поддержку.

Метод анализа иерархий одинаково пригоден как при сравнении факторов, по которым возможно проведение определенных измерений, т.е. возможно их количественное сравнение, так и при сравнении факторов, по которым возможны только суждения.

 

Синтез приоритетов

После построения иерархии и определения величин парных субъективных суждений следует этап, на котором иерархическая декомпозиция и относительные суждения объединяются для получения осмысленного решения многокритериальной задачи принятия решений.

Из групп парных сравнений формируется набор локальных критериев, которые выражают относительное влияние элементов на элемент, расположенный на уровне выше.

Для определения относительной ценности каждого элемента необходимо найти геометрическое среднее и с этой целью перемножить n элементы каждой строки и из полученного результата извлечь корни n-й степени. Полученные числа необходимо нормализовать.

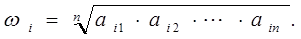
Например, для данных, которые приведены в таблице 4, имеем:

размерность матрицы n =3.

Находим произведения элементов, находящихся в каждой строке:

3_____

1-я строка ω₁ = √1·3·7 = 2,759;

3________

2-я строка ω₂ = √1/3 ·1·3 = 1,0;

3__________

3-я строка ω₃ = √1/7·1/3·1 = 0,362.

 

Проводим нормализацию полученных чисел.

Для этого определяем нормирующий множитель r

r =ω₁ +ω₂ +ω₃ + ………+ ω_n.

И каждое из чисел ω_i делим на r

q_2i = ω_i/r, (i = 1,2,3,...... n).

В результате получаем вектор приоритетов:

q ₂ = (q₂₁, q₂₂, q₂₃, …..q_2n),

где индекс 2 означает, что вектор приоритетов относится ко второму уровню иерархии.

Для рассматриваемого примера нормирующий коэффициент равен:

r = 2,759 + 1,0 + 0,362 = 4,121.

А вектор приоритетов

q₂₁ = ω₁/r = 2,759/2,957 = 0,6697;

q₂₂ = ω₂/r = 1,000/2,957 = 0,243;

q₂₃ = ω₃/r = 0,362/2,957 = 0,088.

Числа q₂₁, q₂₂ и q₂₃ являются компонентами вектора приоритетов критериев К1, К2 и К3 соответственно

q ₂ = (0,67; 0,243; 0,088).

 

 

Подобную процедуру проделываем для всех матриц парных сравнений.

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: