 |
Многоканальные СМО с отказами
|
|
|
|
Одноканальные СМО с отказами
В соответствии с классификацией Кендалла-Башарина такая СМО обозначается M/M/1:0, где символы «M» обозначают простейший входящий поток и поток обслуживания соответственно, «1» – один канал обслуживания, а «0» – отсутствие очереди. Состояние S0 соответствует свободной системе, S1 – состояние, когда единственный канал занят.

1.Предельные вероятности состояний: 𝑝о = 1\ 1 + 𝜌, 𝑝1 = 𝜌 \1 + 𝜌.
2. Вероятностью отказа Pотк = p1
3. Относительная пропускная способность Q, которая отображает относительную долю заявок, получающих обслуживание: 𝑄 = 1 − 𝑃отк = 𝑝0 = 1 \1 + 𝜌
4. Абсолютная пропускная способность A показывает абсолютное количество заявок, получающих обслуживание: 𝐴 = 𝜆𝑄 = 𝜆(1 – Ротк) = 𝜆\ 1 + р
Одноканальные СМО с ограниченной и неограниченной очередями
Одноканальная СМО с ограниченным числом мест для ожидания (очередью) обозначается как M/M/1:m, где m – количество мест в очереди. Размеченный граф состояний:

Состояние S0 обозначает, что система свободна, S1 – занят один канал, S2 – канал занят и одна заявка в очереди, Sm+1 – канал занят и все m мест в очереди также заняты, последующие заявки получат отказ в обслуживании. Таким образом, СМО является гибридной: с очередью и отказами. Интенсивность переходов в предыдущие состояния в отличие от многоканальной системы остается неизменной, т.к. длина очереди не влияет на скорость продвижения заявок по ней
Одноканальные СМО с ограниченной очередью
1. Предельные вероятности состояний:

а в случае ρ = 1 преобразуются к виду

2. Вероятность отказа в обслуживании:

3. Вероятность попадания в очередь складывается из вероятностей попадания на первую, вторую и т.д. позицию в очереди, вплоть до последней, дальше наступает отказ в обслуживании:
|
|
|

4. Средняя длина очереди равна:

При ρ = 1 формула преобразуется к виду:

Одноканальные СМО с ограниченной очередью
5.Среднее число заявок на обслуживании Nобс, которое всегда равно среднему числу занятых каналов nз, в данном случае проще определить по классической формуле:

6. Среднее число заявок в СМО складывается из среднего числа заявок в очереди и среднего числа заявок на обслуживании: 𝑁СМО= 𝑁оч + 𝑁обс; 7. Среднее время ожидания в очереди Tоч находится с помощью формулы Литтла:
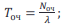
8. Среднее время обслуживания заявок Tобс равно:

9. Среднее время нахождения заявки в СМО равно:

10. Среднее время простоя канала определяется

При m = 0 (очередь отсутствует) все формулы переходят к виду для системы с отказами, а при m®¥ система превращается в систему с неограниченной очередью.
Одноканальные СМО с неограниченной очередью
Согласно классификации Кендалла-Башарина такая СМО обозначается как M/M/1:∞ или сокращенно M/M/1. По-прежнему состояние S0 соответствует свободной системе, S1 – занятому каналу и отсутствию очереди, S2 – занятому каналу и одной заявке в очереди и т.д.

Основные характеристики обслуживания могут быть получены при переходе m®¥ из формул предыдущего раздела (тема 3.2). Однако при r³ 1 возникает ситуация неограниченного роста очереди. Очевидно, что в этом случае поток входящих заявок превышает поток обслуживания и один канал не в состоянии справиться с работой. Такой случай на практике не рассматрива-ют, полагая r< 1.


Многоканальные СМО с отказами
Обозначается такая СМО символами M/M/n:0. Расшифровка состояний при этом следующая: S0 – система свободна, S1 – занят один канал (любой), S2 –заняты два канала (любых), Sn – заняты все n каналов. Интенсивность входящего потока не меняется в зависимости от занятости системы (считаем число источников заявок достаточно большим), а вот интенсивность обслуживания растет пропорционально числу занятых каналов. Это связано с тем, что для перехода системы в предыдущее состояние требуется освобождение не конкретного канала, а любого из занятых, что, естественно, произойдет с большей вероятностью, чем освобождение одного канала.
|
|
|

Расчет основных характеристик, как и во всех остальных случаях, начинается с расчета предельных вероятностей:

Формула для определения вероятности отказа носит название первой формулы Эрланга (B-формулы Эрланга):

Относительная и абсолютная пропускная способности рассчитываются по аналогии с предыдущей системой. Среднее количество занятых каналов nз может быть найдено как отношение абсолютной пропускной способности к интенсивности обслуживания:

Среднее количество заявок, находящихся в системе, NСМО в данном случае равно числу занятых каналов, т.к. каждый канал может единовременно обслуживать только одну заявку, а очереди нет. Коэффициент занятости каналов равен отношению числа занятых каналов к общему числу каналов 𝐾з = 𝑛з 𝑛. Среднее время нахождения заявок в системе TСМО может быть найдено через NСМО по формуле Литтла:

Коэффициент простоя каналов Kп очевидно равен 1–Kз, причем эта величина обозначает еще и вероятность занятости канала Pзк, которая может быть выражена через среднее время занятости канала t зк и среднее время простоя канала t зк

Среднее время занятости канала 𝑡зк = 1 𝜇, тогда среднее время простоя одного канала с учетом и определяется выражением:

|
|
|


