 |
B9 (высокий уровень, время – 3 мин)
|
|
|
|
Тема: Графы. Поиск путей
Что нужно знать:
· если в город R можно приехать только из городов X, Y, и Z, то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть
,
где 
обозначает число путей из вершины A в некоторую вершину Q
· число путей конечно, если в графе нет циклов – замкнутых путей
Пример задания:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение (1 вариант, подстановки):
1) начнем считать количество путей с конца маршрута – с города К
2) будем обозначать через NX количество различных путей из города А в город X
3) общее число путей обозначим через N
4) по схеме видно, что NБ = NГ = 1
5) очевидно, что если в город X можно приехать только из Y, Z, то NX = NY + NZ, то есть нужно сложить число путей, ведущих из A во все города, откуда можно приехать в город X
6) поскольку в K можно приехать из Е, Д, Ж или И, поэтому
N = NК = NД + NЕ + NЖ + NИ
7) в город И можно приехать только из Д, поэтому NИ = NД
8) в город Ж можно приехать только из Е и В, поэтому
NЖ = NЕ + NВ
9) подставляем результаты пп. 6 и 7 в формулу п. 5:
N = NВ + 2NЕ + 2NД
10) в город Д можно приехать только из Б и В, поэтому
NД = NБ + NВ
так что
N = 2NБ + 3NВ + 2NЕ
11) в город Е можно приехать только из Г, поэтому NЕ = NГ так что
N = 2NБ + 3NВ + 2NГ
12) по схеме видно, что NБ = NГ = 1, кроме того, NВ = 1 + NБ + NГ = 3
13) окончательно N = 2NБ + 3NВ + 2NГ = 2·1 + 3·3 + 2·1 = 13
14) Ответ: 13.
Решение (2 вариант, удобная форма записи):
1) начнем считать количество путей с конца маршрута – с города К
2) 
записываем для каждой вершины, из каких вершин можно в нее попасть
|
|
|
К ИДЖЕ
И Д
Ж ВЕ
Е Г
Д БВ
Г А
В АБГ
Б А
3) теперь для удобства «обратного хода» вершины можно отсортировать так[1], чтобы сначала шли все вершины, в которые можно доехать только из начальной точки А:
Б А
Г А
затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки):
В АБГ
Е Г
далее добавляем все вершины, куда можно доехать из А, Б, Г, В и Е:
Д БВ
Ж ВЕ
на следующем шаге добавляем вершину И
И Д
и, наконец, конечную. вершину
К ИДЖЕ
именно в таком порядке мы и будем вычислять количество путей для каждой вершины
4) теперь идем по полученному списку вершин, полагая, что количество вариантов попасть в вершину равно суммарному количеству вариантов попасть в ее непосредственных предшественников.
NБ = 1, NГ = 1
NВ = 1+1+1 = 3, NЕ = 1
NД = 1+3 = 4, NЖ = 3 + 1 = 4
NИ = 4,
N = NК = 4 + 4 + 4 + 1 = 13
5) заметим, что вершины можно и не сортировать специально, а просто выбирать возможный порядке вычисления: проверять, какие значения известны и какие можно рассчитать с их помощью на следующем шаге
6) Ответ: 13.
| Возможные ловушки и проблемы: · очень важна аккуратность и последовательность; сначала идем от конечной точки к начальной, выписывая все вершины, из которых можно приехать в данную; затем идем обратно, определяя числовые значения · построение полного дерева маршрутов – занятие трудоемкое и достаточно бесперспективное, даже грамотные учителя информатики здесь в большинстве случаев что-то забывают и ошибаются |
Решение (3 вариант, перебор вершин по алфавиту):
1) Запишем вершины в алфавитном порядке и для каждой из них определим, из каких вершин можно в нее попасть
Б А
В АБГ
Г А
Д БВ
Е Г
Ж ВЕ
И Д
К ИДЖЕ
2) теперь определяем количество путей; сначала ставим 1 для тех вершин, в которые можно проехать только из начальной (А):
| вершина | откуда? | N |
| Б | А | |
| В | АБГ | |
| Г | А | |
| Д | БВ | |
| Е | Г | |
| Ж | ВЕ | |
| И | Д | |
| К | ИДЖЕ |
3) затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки):
|
|
|
| вершина | откуда? | N |
| Б | А | |
| В | АБГ | |
| Г | А | |
| Д | БВ | |
| Е | Г | |
| Ж | ВЕ | |
| И | Д | |
| К | ИДЖЕ |
4) следующий шаг
| вершина | откуда? | N |
| Б | А | |
| В | АБГ | |
| Г | А | |
| Д | БВ | |
| Е | Г | |
| Ж | ВЕ | |
| И | Д | |
| К | ИДЖЕ |
5) и последние 2 шага
| вершина | откуда? | N |
| Б | А | |
| В | АБГ | |
| Г | А | |
| Д | БВ | |
| Е | Г | |
| Ж | ВЕ | |
| И | Д | |
| К | ИДЖЕ |
6) Ответ: 13.
Решение (4 вариант, перебор всех путей с начала, А. Яфарова):
1) запишем все вершины, в которые есть прямой путь из вершины A: Б, В и Г; получается три начальных отрезка:
АБ, АВ, АГ
2) рассмотрим маршрут АБ: из Б можно ехать в В и Д, поэтому получаем два маршрута:
АБ В, АБ Д
3) рассматриваем конечные точки этих маршрутов: из В можно ехать в Д и Ж, а из Д – в И и К:
АБВ Д, АБВ Ж, АБД И, АБД К
4) снова смотрим на конечные точки: из Д едем в И и К, из Ж и И – только в К:
АБВД И, АБВД К, АБВЖ К, АБДИ К, АБДК
5) из И едем только в К, таким образом, все возможные маршруты, содержащие участок АБ, доведены до конечной точки К, всего 5 таких маршрутов:
АБВДИ К, АБВДК, АБВЖК, АБДИК, АБДК
6) затем аналогично рассматриваем маршруты, которые начинаются с АВ:
АВД, АВЖ
АВДИ, АВДК, АВЖК
АВДИК, АВДК, АВЖК
всего 3 маршрута
7) наконец, остается рассмотреть маршруты, которые начинаются с АГ:
АГВ, АГЕ
АГВД, АГВЖ, АГЕЖ, АГЕК
АГВДИ, АГВДК, АГВЖК, АГЕЖК, АГЕК
АГВДИК, АГВДК, АГВЖК, АГЕЖК, АГЕК
всего 5 маршрутов
8) складываем количество маршрутов для всех начальных участков: 5 + 3 + 5 = 13
9) Ответ: 13.
| Возможные проблемы: · при большом количестве маршрутов легко запутаться и что-то пропустить |
Задачи для тренировки [2]:
1) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
2) рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
|
|
|
3) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
4) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
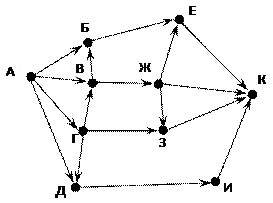
5) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
6) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
7) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
8) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
9) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
10) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
[1] Такая процедура называется топологической сортировкой графа.
[2] Источники заданий:
1. Тренировочные работы МИОО 2011-2012.
2. Авторские разработки.
|
|
|
