Знаки значений основных тригонометрических функций по четвертям круга.

ТеМА № 6.

РАСЧЁТ ПЛАВАНИЯ СУДНА ПО ОРТОДРОМИЯ

Содержание лекции: 1. Ортодромия и ее элементы.

2. Основные формулы ортодромии. Способы ее задания.

3. Формулы для расчета параметров плавания по ортодромии по

Координатам двух точек ортодромии.

Ортодромия и ее элементы.

Часть дуги большого круга, проходящего через две точки на земной поверхности, являющуюся кратчайшим расстоянием между этими точками, называется ортодромией (в переводе с греческого – «прямой бег»). На картах меркаторской проекции ортодромия имеет вид кривой, обращенной выпуклостью в сторону ближайшего полюса, а на картах в гномонической проекции – вид прямой линии.

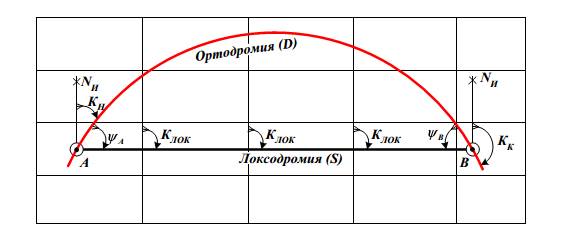
Рисунок 6.1. – Ортодромия и локсодромия на карте Меркаторской проекции.

При небольших морских переходах разность в длине между локсодромией и ортодромией незначительна, Из-за удобства плавания постоянным курсом в практической навигации таким увеличением длины пути пренебрегают и совершают морские переходы постоянными курсами.

Чтобы изобразить кратчайший путь на карте меркаторской проекции, и в действительности на судне по максимально возможно кратчайшему пути, необходимо, чтобы курсы судна были отрезками локсодромий, начинающимися и заканчивающимися своими крайними точками на линии ортодромии. Сумма таких отрезков локсодромий даст максимально близкий к ортодромическому путь судна, и, в то же время, позволит судну максимально длительное время плыть постоянным курсом.

Рисунок 6.2. – Пример плавания судна по хордам ортодромии.

 

Любую ортодромию и плавание по ней можно охарактеризовать следующими элементами (рисунок 6.3.):

1. Начальная точка ортодромии ( точка А с координатами φ_А; λ_А).
2. Начальный курс плавания по ортодромии (К_Н) – двугранный угол между северной частью истинного меридиана в точке А и ортодромией в этой же точке, или плоским углом между касательными к меридиану и к ортодромии точке А;
3. Конечная точка ортодромии (точка В с координатами φ_В; λ_В);
4. Конечный курс плавания по ортодромии (К_К) – двугранный угол между северной частью истинного меридиана в точке В и ортодромией в этой же точке, измеряемый плоским углом между касательными к меридиану и к ортодромии точке В;
5. Точка λ₀ – точка пересечения ортодромии с земным экватором (φ₀ = 0°; λ₀);
6. Угол К₀ – двугранный угол между северной частью истинного меридиана в точке φ₀ = 0°, λ₀ и ортодромией в этой же точке, измеряемый плоским углом между касательными к меридиану и к ортодромии точке φ₀ = 0°, λ₀;
7. Точка вертекса – точка ортодромии, имеющая наибольшее значение широты (φ_V). Это точка «перегиба» ортодромии и курс судна в этой точке К_V = 90° (при плавании судна в восточном направлении) или К_V = 270°(при плавании судна в западном направлении). Ортодромия касательная к параллели в точке вертекса.

Рисунок 6.3. – Положение ортодромии на Земной поверхности и её элементы.

Основные формулы ортодромии. Способы ее задания.

Решая задачу плавания по ортодромии, которая является частью дуги большого круга на Земной поверхности, мы опираемся на основные понятия сферической геометрии.

Рассмотрим сферический треугольник АР_NВ, элементами которого являются (рисунок 6.4):

1. Стороны треугольника АР_NВ:

- АР_N → (90 – φ_А);

- Р_NВ → (90 – φ_В);

- АВ → D (длина ортодромии).

2. Углы треугольника АР_NВ:

- ے Р_NАВ → К_Н (начальный курс плавания по ДБК);

- ے Р_NВА → 180 – К_К (конечный курс плавания по ДБК);

- ے АР_NВ → ∆λ = λ_В - λ_А (разность долгот между конечной В и начальной А

Точками ДБК).

Рисунок 6.4. – Сферический треугольник ортодромии.

Из сферической тригонометрии известно «…если в сферическом треугольнике известны три элемента то, по формулам сферической тригонометрии, можно определить и все остальные…».

Применяя формулу «косинуса стороны» («…косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…») можно определить длину ортодромии D между любыми двумя ее точками (т. А и т. В), координаты которых известны, то есть:

CosD = cos (90°-φ_A) – cos (90°-φ_B) + sin (90°-φ_A) – sin (90°-φ_B) – cos (λ_B - λ_A)

или, после преобразования:

CosD = sinφ_A x sinφ_B + cosφ_A x cosφ_B x cos (λ_B - λ_A)

Применяя формулу «котангенса угла» («…произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних частей…») можно определить значение начального К_Н и конечного К_К курсов плавания по ортодромии.

ctgK_H = cosφ_A x tgφ_B x cosec (λ_B –λ_A) - sinφ_A x ctg(λ_B –λ_A)

ctgK_K = - tgφ_A x cosφ_B x cosec (λ_B –λ_A) + sinφ_B x ctg(λ_B –λ_A)

Аналогично определяем остальные величины:

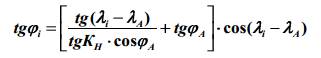
или

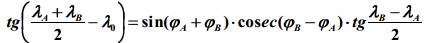
Где:

 

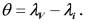
Ортодромия может быть задана одним из 4-х способов:

- по координатам любых двух ее точек (т. А: φ_А λ _А и т. В: φ_В λ_В) при условии, что эти точки не лежат на противоположных концах земного диаметра;

- по координатам любой точки ортодромии (φ_А λ_А, φ_i λ _i, φ_В λ_В …) и направлению (курсу) ортодромии в этой точке (К_Н или К_i или К_К);

- по долготе (λ₀) точки пересечения ортодромии с экватором и направлению ортодромии в этой точке (К₀);

- по координатам точки V – вертекса (φ_V λ_V ортодромия в этой точке касательна к параллели).

3. Формулы для расчета параметров плавания по ортодромии по координатам двух точек ортодромии

1. Плавание по ортодромии можно рассчитать по формуле:

CosD = Sin φ_НSin φ_К+Cos φ_НCos φ_КCos(λ_К – λ_Н); (1)

2. Начальный курс плавания по ортодромии:

CtgK_Н = tg φ_КCos φ_НCosec(λ_К – λ_Н)–Sinφ_Нctg(λ_К – λ_Н); (2)

3. Конечный курс плавания по ортодромии:

Ctg К_К = – tg φ_НCos φ_КCosec(λ_К – λ_Н)+Sin φ_Кctg(λ_К – λ_Н); (3)

Где: D – длина пути по ортодромии;

φ_Н; λ_Н – координаты точки отхода;

φ_К; λ_К – координаты точки прихода;

λ_К – λ_Н – РД точек отхода и прихода.

При выполнении вычислений по приведенным формулам, их необходимо исследовать на знаки, руководствуясь такими правилами:

– северная широта → все функции широты имеют знак плюс;

– южная широта → Sin широты имеет знак минус, Cos широты имеет знак плюс;

– знак разности долгот λ_К – λ_Н определяется направлением движения судна. При движении судна к востоку λ_К – λ_Н имеет знак плюс, при движении на запад – минус;

Знаки значений основных тригонометрических функций по четвертям круга.

Таблица 1.

Четверти	Функции
Sin α	Cos α	tg α	ctg α
I	+	+	+	+
II	+	–	–	–
III	–	–	+	+
IV	–	+	–	–

Функция Sin α нечетная: → Sin (– α) = – Sin α; Значение Sin α соответствует ординате единичного радиус-вектора.

Функция Cos α четная: → Cos (– α) = Cos α; Значение Cos α соответствует абсциссе единичного радиус-вектора.

Функция tg α нечетная: → tg(– α) = – tg α; При α = 0° → tg α = 0; при увеличении или уменьшении угла α от 0° → tg α возрастает до бесконечности.

Функция ctg α нечетная: → ctg (– α) = – ctg α; При α =90° → ctg α = 0; При увеличении ли уменьшении угла α от 90° → ctg α возрастает до бесконечности.

Функция Sec α четная: → Sec (– α) = Sec α; Функция Sec α ни при каких значениях угла α не обращается в нуль.

Функция Cosec α нечетная: → Cosec α (– α) = – Cosec α; Функция Cosec α ни при каких значениях угла α не обращается в нуль.

Формулы приведения. Вычисления значений тригонометрических функций любого угла сводится к вычислению значений тригонометрических функций острого угла по следующим правилам:

1) Если угол положительный и больше 2π, то функция синус и косинус данного угла приводятся к функциям угла большего нуля и меньшего 2π, по формулам:

Sin (α+2πn) = Sin α;

Cos (α+2πn) = Cos α.

2) Если угол отрицательный, то тригонометрические функции данного угла приводятся к тригонометрическим функциям положительного угла по формулам:

Sin (– α) = – Sin α; Cos (– α) = Cos α;

tg (– α) = – tg α; ctg (– α)= – ctg α.

3) Тригонометрические функции угла, большего π/2 и меньшего 2π, приводятся к тригонометрическим функциям острого угла по формулам приведения (См. Таблицу 5.4.2.), которые можно сформулировать в виде следующего правила:

Если в формуле приведения угол α вычитается из π/2 или прибавляется к π/2, взятому нечетное число раз, то приводимая функция меняется на кофунцию ( Косинус является кофункцией по отношению к синусу, и наоборот. Другая пара кофункций – тангенс и котангенс.); если же π/2 взято четное число раз, то название приводимой функции сохраняется. При этом перед приведенной функцией ставится тот знак, который имеет приводимая функция в соответствующей четверти, если считать угол α острым.

Таблица 2.

Ф У Н К Ц И Я	А р г у м е н т
π + α = β 180° + α = β	π – α = β 180° – α = β
Sin β	– Sin α	+ Sin α
Cos β	– Cos α	– Cos α
tg β	+ tg α	– tg α
ctg β	+ ctg α	– ctg α

Проверку расчетов К_Н и К_К можно выполнить по следующим формулам:

Sin К_Н = Cos φ_К Sin(λ_К – λ_Н)CosecD (4)

 

Sin К_К = Cos φ_Н Sin(λ_К – λ_Н)CosecD (5)

 

Пример. Вычислить D, К_Н и К_К ортодромии АВ:

 

Дано: φ_Н = 41°28,0'N; λ_Н = 143°26,0'E;

φ_К = 37°45,0'N; λ_К = 122°50,0'W;

1. Рассчитываем разность долгот: РД = (λ_К – λ_Н)

λК	–122°50,0'
–λН	+143°26,0'
РД	–266°16,0'
РД	+ 93°44,0'

 

РД = 93°44,0' к E.

 

2. Рассчитываем плавание по ортодромии:

CosD = Sin φ_НSin φ_К+Cos φ_НCos φ_КCos(λ_К – λ_Н);

φН	41°28,0'N	Sin	+0,66218	Cos	+0,74934
φК	37°45,0'N	Sin	+0,61222	Cos	+0,79069
РД	93°44,0' к E = = 86°16,0'			Cos	–0,06511
		+ I	+0,40540	II	–0,03858
		+ II	–0,03858
		Cos Dорт	+ 0,36682

D _орт = 68°28,8'

D _орт = 68°28,8' = 4108,8' = 4108,8 миль

D_орт = 4109,0 миль

3. Рассчитываем начальный курс ортодромии:

CtgK_Н = tg φ_К Cos φ_Н Cosec(λ_К – λ_Н) – Sinφ_Н ctg(λ_К – λ_Н);

φН	41°28,0'N	Cos	+ 0,74934	Sin	+ 0,66218
φК	37°45,0'N	tg	+ 0,77428
РД	93°44,0' к E = 86°16,0' (β)	Cosec	+ 1,00213	Ctg	– 0,06525
		+ I	+ 0,58143	II	– 0,04432
		– II	– 0,04432
		Ctg КН	+ 0,62575

 

К_Н = 57°,0 NE = 57,0°;

К_Н = 57,°0.

Проверим начальный курс ортодромии по формуле:

Sin К_Н = Cos φ_К Sin(λ_К – λ_Н)CosecD

φК	37°45,0'N	Cos	+ 0,79069
РД	93°44,0' к E = 86°16,0'	Sin	– 0,99788
Dорт	68°28,8'	Cosec	– 1,07493
		Sin КН	+ 0,84813

К_Н = 58°,0 NE = 58,0°;

К_Н = 58,°0.

4. Рассчитываем конечный курс ортодромии:

Ctg К_К = – tg φ_Н Cos φ_К Cosec(λ_К – λ_Н)+Sin φ_К ctg(λ_К – λ_Н);

φН	41°28,0'N	tg	+ 0,88369
φК	37°45,0'N	Cos	+ 0,79069	Sin	+ 0,61222
РД	93°44,0' к E = 86°16,0' (β)	Cosec	+ 1,00213	Ctg	– 0,06525
		– I	–0,70021	+ II	–0,03995
		+ II	–0,03995
		Ctg КК	+ 0,66001

К_К = (180,°0 – 56°34,5' SE) = (180,°0 – 56°34,5') = 123°,5

К_К = 123,5°.

Проверим конечный курс ортодромии по формуле:

Sin К_К = Cos φ_Н Sin(λ_К – λ_Н)CosecD

φН	41°28,0'N	Cos	+ 0,66218
РД	93°44,0' к E = 86°16,0'	Sin	+ 0,99788
Dорт	68°28,8'	Cosec	+ 1,07493
		Sin КК	+ 0,71029

 

К_К = 58°,0 SE = (180,°0 – 58,0°) = 122,°0;

К_К = 122,°0.

Вопросы для проверки понимания материала лекции.

1. Что такое ортодромия?

2. Какой вид на морской навигационной карте Меркаторской проекции имеет ортодромия?

3. Как выглядит ортодромия на земной поверхности?

4. Как выглядит ортодромия на карте в гномонической проекции?

5. Назовите основные элементы ортодромии.

6. Назовите основные формулы для расчета параметров плавания по ортодромии?

Литература для самостоятельного изучения, имеющаяся в технической библиотеке ИФ ОНМА:

 

1. Паластров В.Ф.и др. «Навигация», стр. 111 – 114, 697-724

2. Лесков М.М. и др. «Навигация», стр. 59 – 62, 333 – 343.

3. Дмитриев В.И. и др. «Навигация и лоция», стр. 16 – 23.

4. Конспект лекций по предмету «Навигация и лоция».

5. Дополнительный материал по теме учащиеся подбирают

самостоятельно.

Рекомендуемая литература: Михайлов В.С., Кудрявцев В.Г., стр. 522 – 534.

 

Поделиться:

Воспользуйтесь поиском по сайту: