 |
Name Size Bytes Class Attributes
|
|
|
|
Лабораторная работа № 1
ВЫЧИСЛЕНИЯ В КОМАНДНОМ ОКНЕ СИСТЕМЫ MATLAB
Цель работы. Изучить основные математические операции и математические функции системы MATLAB.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Название системы (пакета) MATLAB происходит от английского выражения Matrix Laboratory – матричная лаборатория. В основе лежат математические и технические вычисления. В этой системе оптимизированы операции с массивами, и, соответственно, с матрицами (двумерные массивы). Даже одно число воспринимается как массив размером 1´1 – одна строка, один столбец. Система MATLAB состоит из ядра, специализированных пакетов (ToolBox) и пакета Simulink (соответствующих версий). MATLAB – это интерпретатор. В общем случае он не создает исполняемых файлов (приложений).

Рассмотрим запуск MATLAB на примере версии R2007b. Он осуществляется традиционно: пуск – Все программы – MATLAB – R2007b – MATLAB R2007b. Могут быть и другие версии, например, MATLAB R2008a, MATLAB R2007a, MATLAB 6.5. Должно появиться окно, показанное на рис.1.1.
Рис. 1.1. Стартовая страница MATLAB R2007b по умолчанию

Выделенное активно окно – Command Window является основным для расчетов. В нем можно производить большинство вычислительных расчетов и выполнять графические построения. Приглашение к работе осуществляется миганием курсора после символа >>. Можно установить только командное окно (Command Window Only). Для этого из меню Desktop выбрать опции, показанные на рис. 1.2.
Рис. 1.2. Выбор опции только командного окна в MATLAB R2007b
Результат того или иного вычисления в командном окне MATLAB осуществляется после нажатия клавиши Enter. При этом результат может быть записан в ячейку памяти с соответствующим именем, как говорят с присвоением результата. Если присвоения результата не производится, то в командном окне MATLAB используется сокращенная запись ans (от английского answer – отвечать, ответ), после чего выводится результат вычисления. Комментарии осуществляются после символа процента %.
|
|
|
Система MATLAB богата большим набором встроенных функций, которые могут возвращать результат, могут выполнять графические построения – 2D и (или) 3D графика. Справку о той или иной функции можно получить, набрав в командном окне help имя_функции (например, help sqrt).
В MATLAB можно также создавать графический интерфейс пользователя, например, с помощью утилиты guide. Только в общем случае интерфейс будет функционировать при открытой системе MATLAB.
Для версии MATLAB R2011b соответствующие окна показаны на рис. 1.3, рис. 1.4.

Рис. 1.3. Стартовая страница MATLAB R2011b
Рис. 1.4. Выбор опции командного окна в MATLAB R2011b
ПРАКТИЧЕСКАЯ ЧАСТЬ
1. Основные математические операции
Рассмотрим примеры, которые будет выполнять в командном окне.
Сначала выполним операции сложения и вычитания:
| >> 2+2 % без присвоения результата ans = >> 7-5 % без присвоения результата ans = >> a=6+7+8 % присвоение результата в ячейке памяти с именем а a = % Обращение к ячейке под именем а >> a a = % Вычисления без вывода на экран промежуточных результатов >> a1=2+4;b1=3+4;c1=5+3; >> A=a1+b1+c1 A = >> B = 2*A; % без вывода, точка с запятой подавляет вывод >> B % обращение к переменной B B = |
Комментарии располагаются после знака процента %. Имена переменных должны начинаться с букв латинского алфавита.
Можно произвести очистку командного окна с помощью команды clc. При этом все переменные и объекты остаются в памяти, в рабочей области текущей директории MATLAB. Для очистки памяти используется команда clear, например,
>> clear B
Тогда при обращении к переменной В получим следующее сообщение:
>> B
??? Undefined function or variable 'B'.
|
|
|
То есть, неизвестная функция или переменная 'B'. Можно произвести очистку рабочей области от всех переменных. Для этого следует записать
>> clear all
Можно выполнить выборочную очистку памяти, удаление некоторых переменных, например
>> a = 6, b = 7, c = 9.9
a =
b =
c =
9.9000
>> clear a c
>> a
??? Undefined function or variable 'a'.
>> b
b =
>> c
??? Undefined function or variable 'c'.
В системе MATLAB следует учитывать регистр клавиатуры. Заглавные и строчные буквы имеют самостоятельное значение (как в языках программирования С/С++, C# и др. С-подобные языки). Операции умножения и деления:
| >> 2*2 % без присвоения результата ans = >> 7/2 % без присвоения результата ans = 3.5000 >> b = 3 * 8 % с присвоением результата в ячейку с именем b b = >> c=2*3 % результат записывается в ячейку с именем с c = >> d = b / c % результат записывается в ячейку с именем d d = % Простейшее математическое выражение B = 2 * 3 + 4 + (10*10 - 90)*(2 + 4)/(2 + 2) B = |
Как видно из примеров запись математических выражений может быть выполнена с пробелами (в стиле С/C++).
Примеры возведения в степень и извлечение квадратного корня и других степеней корней:
| >> 2^2 % два в квадрате ans = >> C = 2^3 % два в кубе (два в третьей степени) C = >> sqrt(16) % корень квадратный из числа 16 ans = >> 16^(1/2) % число 16 в степени одна вторая ans = >> N = sqrt(16); n = sqrt(N); >> M = n^3 M = >> M^(1/sqrt(9)) % равносильно корню кубическому из числа 8 ans = % Смотрите помощь help sqrt и help ^ % Вычисление корня кубического из действительного числа >> a = -27; b = nthroot(a, 3), b2 = a^(1/3) b = -3 b2 = 1.5000 + 2.5981i % см. help nthroot |
Примеры задания ряда чисел с заданным шагом с помощью оператора двоеточие, т. е. одномерных массивов:
| >> t = 0: 0.5: 3 % 0.5 - шаг t = 0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 >> m = 2.5; p = 1; K = 11; T = p: m: K T = 1.0000 3.5000 6.0000 8.5000 11.0000 >> Y = 1: 7 % по умолчанию шаг принимается равным единице Y = 1 2 3 4 5 6 7 >> sqrt(Y) ans = 1.0000 1.4142 1.7321 2.0000 2.2361 2.4495 2.6458 |
Как видно из выше приведенного примера функция извлечения квадратного корня может быть использована для массивов данных. Если требуется объединить в массив числа в произвольном порядке, о тогда следует использовать квадратные скобки, например
>> M = [-9.9, 123, 0, 678, -1]
M =
-9.9000 123.0000 0 678.0000 -1.0000
Элементы массива могут разделяться также пробелами.
|
|
|
Примеры сортировки числовых массивов
| >> r1 = [4 7 2 1 9 10 3] % задание вектора-строки чисел r1 = 4 7 2 1 9 10 3 >> % r1 = [4, 7, 2, 1, 9, 10, 3] % ввод чисел через запятую >> sort(r1) % см. help sort ans = 1 2 3 4 7 9 10 >> sort(r1') %% сортировка для транспонированного массива ans = >> r2 = [4; 7; 2; 1; 9; 10; 3]; % задание вектора-столбца >> sort(r2) ans = |
По умолчанию функция sort сортирует по возрастанию. В этой функции можно задать вид сортировки. В частности, по возрастанию через служебную строку 'ascend', по убыванию – через строку 'descend'.
Пример сортировки по убыванию:
| >> r1 = [4, 7, 2, 1, 9, 10, 3]; % без вывода на дисплей >> sort(r1, 'descend') ans = 10 9 7 4 3 2 1 |
Задание 1
1. Проверьте сортировку по убыванию для одномерного массива с отрицательными и положительными вещественными числами без использования служебной строки 'descend'.
Пример формирования двухмерного массива
| >> R = [r2, sort(r2)] % формирование двухмерного массива R = 4 1 7 2 2 3 1 4 9 7 10 9 3 10 >> size(R) % определение размерности массива (см. help size) ans = 7 2 |
Полученный результат означает, что массив имеет 7 строк и 2 столбца.
Задание 2
1. Сформируйте массив, состоящий из заданного вектор-столбца чисел, отсортированного по возрастанию заданных чисел и отсортированного по убыванию заданных чисел. Проверьте размерность сформированного массива.
2. Создайте произвольную матрицу из вещественных чисел размера 4´3, полученную матрицу отсортируйте по строкам и по столбцам с помощью функции sort.
2. Элементарные математические функции
Справку по элементарным математическим функциям, которые реализуются системой MATLAB, можно получить по справке из командного окна (командной строки). Для этого следует набрать help elfun. Практически все функции могут быть использованы для массивов. Рассмотрим некоторые «элементарные» функции.
2.1. Показательная функция pow2
Функция pow2 используется для возведения числа 2 в какую-либо степень (от действительных и (или) комплексных чисел). Справка по этой функции: help pow2
Примеры с функцией pow2
|
|
|
| >> pow2(2) % соответствует 2^2 ans = >> a = pow2(3) % соответствует 2^3 a = >> b = pow2(5) b = >> B = pow2(1/2) % соответствует корню квадратному из двух B = 1.4142 >> b,B % для проверки содержимого ячеек памяти b = B = 1.4142 >> c=pow2(3+4*i) % соответствует 2^(3+4i), i — мнимая единица c = -7.4615 + 2.8855i >> d=pow2(3,4) % соответствует 3*2^4, показатель - целое число d = >> D = pow2(3.5,2) % соответствует 3.5*2^2 D = >> M = pow2([3.5,2,5,10],2) M = 14 8 20 40 |
В последнем примере показана возможность функции pow2 по работе с массивами. Можно использовать, например, двухмерные массивы.
2.2. Экспоненциальная функция exp
Справка по функции exp: help exp
Примеры с функцией exp
| >> fprintf('\n\t e = %0.16f\n', exp(1)) e = 2.7182818284590455 >> exp(1) ans = 2.7183 >> exp([1,2,3,4,5]) % от массива чисел ans = 2.7183 7.3891 20.0855 54.5982 148.4132 |
В примере использована функция fprintf, предназначена в общем случае для форматированного вывода данных различных типов в файл. В данном случае она была использована для вывода данных в командное окно MATLAB. Спецификатор формата %0.16f означает, что не отводится места для выводимого числа (цифра 0), сохраняются 16 цифр после десятичной точки, использован символ горизонтальной табуляции, т. е. \t и осуществлен перевод на новую строку с помощью, так называемой эскейп-последовательности \n. Спецификатор формата f предназначен для вещественных чисел.
2.3. Логарифмические функции log, log2, log10, reallog
Примеры с логарифмическими функциями
| >> log(exp(1)), log2(8), log10(10000) ans = ans = ans = >> log(1), log2(1), log10(1) ans = ans = ans = >> log(-exp(1)), reallog(-exp(1)) ans = 1.0000 + 3.1416i ??? Error using ==> reallog Reallog produced complex result. |
Функция log – это натуральный логарифм от чисел. Функция log2 – это логарифм от чисел по основанию 2. Функция log10 – это десятичный логарифм от чисел. Если натуральный логарифм от отрицательного числа возвращает комплексное число, то функция reallog возвращает сообщение об ошибке, поскольку натуральный логарифм от отрицательного числа не определен (как это было в средней школе). Приведенные функции могут рассчитывать значение логарифма от каждого элемента заданного массива чисел.
Задание 3
1. Подготовить выражение для вычисления логарифма числа по основанию, например, 3, 4, 5. Выполнить проверочный тест.
2.4. Тригонометрические функции
В новых версиях MATLAB тригонометрические функции могут быть использованы как для чисел, представленных в радианах, так и для чисел, представленных в градусах угловых. Например, sin(pi/2), sind(90), где pi/2 есть p/2. В MATLAB имеются обратные тригонометрические функции, гиперболические функции, обратные гиперболические функции (см. help elfun).
Примеры с основными тригонометрическими функциями:
|
|
|
| >> disp([sin(pi/2),sind(90),sind(30),cos(pi),cosd(0),cos(pi/3)]) 1.0000 1.0000 0.5000 -1.0000 1.0000 0.5000 >> [tan(pi/4),tand(45),cot(pi/4),cotd(45)] ans = 1.0000 1.0000 1.0000 1.0000 >> sin([pi/6, pi/2, pi]) % от массива чисел ans = 0.5000 1.0000 0.0000 |
В данных примерах использованы функции синуса, косинуса, тангенса и котангенса, аргументы которых радианы и градусы угловые. Все тригонометрические функции используются также для работы с массивами, как одномерными, так и многомерными.
Задание 4
1. Сформировать квадратную матрицу, элементами которой являются тригонометрические функции sind, cosd, tand, cotd от таких значений, чтобы они возвращали числа 0.5000, т. е. с точностью до четырех знаков после десятичной точки.
Примеры с обратными тригонометрическими функциями
| >> % арксинусы и арккосинусы >> ASC = [asin(0.5), asind(0.5), acos(0.5), acosd(0.5)] ASC = 0.5236 30.0000 1.0472 60.0000 >> % для проверки >> [sin(ASC(1)), sind(ASC(2)), cos(ASC(3)), cosd(ASC(end))] ans = 0.5000 0.5000 0.5000 0.5000 >> % арктангенсы и арккотангенсы >> ATK = [atan(1), atand(1), acot(1), acotd(1)] ATK = 0.7854 45.0000 0.7854 45.0000 >> % для проверки >> [tan(ATK(1)), tand(ATK(2)), cot(ATK(3)), cotd(ATK(end))] ans = 1.0000 1.0000 1.0000 1.0000 |
В примерах приведено обращение к элементам массивов ASC и ATK, соответственно. Зарезервированное слово end означает, что обращение производится к последнему элементу массива.
Область определения функций asin(x), acos(x) для действительных значений лежит в интервале [–1; 1], т. е. х Î [–1; 1]. Соответственно, область значений этих функций лежит в интервале [–p/2; p/2].
Область определения функций atan(x), acot(x) есть вся числовая ось, а область значений этих функций лежит в интервале [–p/2; p/2].
Примеры с гиперболическими функциями
| >> sinh(1:6) % синус гиперболический ans = 1.1752 3.6269 10.0179 27.2899 74.2032 201.7132 >> cosh(1:6) % косинус гиперболический ans = 1.5431 3.7622 10.0677 27.3082 74.2099 201.7156 >> tanh(1:7) % тангенс гиперболический ans = 0.7616 0.9640 0.9951 0.9993 0.9999 1.0000 1.0000 >> coth(1:2:12) % котангенс гиперболический ans = 1.3130 1.0050 1.0001 1.0000 1.0000 1.0000 |
Гиперболические функции могут быть рассчитаны по следующим формулам:




Примеры с обратными гиперболическими функциями
| >> % asinh- арксинус гиперболический, >> % acosh- арккосинус гиперболический >> ASCH = [asinh(0.678), asinh(6.78), acosh(1.678), acosh(6.78)] ASCH = 0.6346 2.6125 1.1071 2.6016 >> % проверка >> [sinh(ASCH(1)), sinh(ASCH(2)),cosh(ASCH(3)) cosh(ASCH(4))] ans = 0.6780 6.7800 1.6780 6.7800 >> % atanh - обратный гиперболический тангенс >> % acoth - обратный гиперболический котангенс >> ATCH = [atanh(0.1), atanh(1), acoth(-1), acoth(123)] ATCH = 0.1003 Inf -Inf 0.0081 >> % проверка >> [tanh(ATCH(1)), tanh(ATCH(2)), coth(ATCH(3)), coth(ATCH(4))] ans = 0.1000 1.0000 -1.0000 123.0000 |
В результатах встретилась зарезервированная величина Inf (или inf), которая соответствует как бы бесконечности.
Обратные гиперболические функции могут быть рассчитаны по следующим формулам:


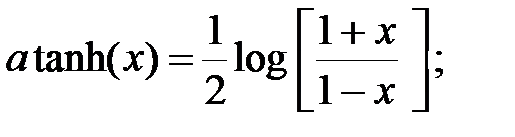
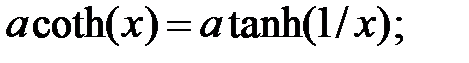
По приведенным формулам можно определить область определения каждой из обратных гиперболических функций.
Задание 5
1. Напишите выражения, реализующие гиперболические функции по приведенным формулам.
2. Напишите выражения, реализующие обратные гиперболические функции по приведенным формулам.
В MATLAB имеются еще следующие встроенные тригонометрические функции: sec, secd (секанс), asec, asecd (арксеканс), sech (секанс гиперболический), asech (арксеканс гиперболический), csc, cscd (косеканс), acsc, acscd (арккосеканс), csch (косеканс гиперболический), acsch (аркокосеканс гиперболический). По ним имеются справки, например, help sec.
2.5. Округления чисел
Примеры округления чисел
| >> % Округление к числу, ближайшего к нулю. Отбрасывание дробной части >> % Функция fix (см. help fix) >> [fix(6.78), fix(-6.78), fix(0.001), fix(-0.001)] ans = 6 -6 0 0 >> % Округление к меньшему числу (в сторону минус бесконечность) >> % Функция floor (см. help floor) >> [floor(6.78), floor(-6.78), floor(-0.001), floor(1.678)] ans = 6 -7 -1 1 >> % Округление в сторону ближайшего целого числа >> % Функция round (см. help round) >> [round(6.7),round(-6.7),round(-0.01),round(1.6),round(1.4)] ans = 7 -7 0 2 1 >> %% Округление в сторону плюс бесконечность >> %% Функция ceil (см. help ceil) >> [ceil(6.1),ceil(-6.1),ceil(0.01),ceil(1.23),ceil(1.6)] ans = 7 -6 1 2 2 |
Задание 6
1. В качестве округляемого числа примите X.YY, где Х – номер месяца, когда вы родились, YY – день месяца. Сформируйте массив в виде вектора-столбца с элементами, состоящих из функций fix(X.YY), floor(X.YY), round(X.YY), ceil(X.YY). Выведите результат в командное окно MATLAB.
2.6. Функции вычисления остатка от деления mod, rem
Примеры вычисления остатков от деления
| >> %% Функция вычисления остатка после деления, модуль – термин >> %% из модулярной, целочисленной арифметики >> %% Функция mod(см. helpmod) >> [mod(2,12), mod(-2,12), mod(-2,-12), mod(11,12), mod(13,12)] ans = 2 10 -2 11 1 >> [mod(3,0), mod(0,3), mod(0,0)] ans = 3 0 0 >> %% Функция вычисления остатка после деления >> %% Функция rem(см. helprem) >> [rem(2,12), rem(-2,12), rem(-2,-12), rem(11,12), rem(13,12)] ans = 2 -2 -2 11 1 >> [rem(3,0), rem(0,3), rem(0,0)] ans = NaN 0 NaN |
Последний результат со значением NaN означает, что это не число (от англ. Not–a–Number). Функции mod и rem дают одинаковый результат для положительных аргументов.
2.7. Функции для работы с простыми числами
Функция primesформирует список простых чисел. Функция isprime проверяет простое ли число. Функция factor разлагает число на простые множители.
Примеры с функциями primes, isprime, factor
| >> primes(21) %% см. help primes ans = 2 3 5 7 11 13 17 19 >> primes(-21) ans = Empty matrix: 1-by-0 >> isprime(123) ans = >> isprime(113) ans = >> isprime(1:9) ans= 0 1 1 0 1 0 1 0 0 >> isprime([1,3,7,9,13,17,19,21]) % для вектора-строки ans = 0 1 1 0 1 1 1 0 >> isprime([1,3,7,9,13,17,19,21]') % ' - транспонирование ans = >> primes(2^4) ans = 2 3 5 7 11 13 >> factor(123) %% разложение числа 123 на простые множители ans = 3 41 >> 3 * 41 %% для проверки ans = |
В одном из примеров получился ответ Emptymatrix. Это означает, что результат есть пустая матрица.
Задание 7
1. Проверьте, является ли год вашего рождения простым числом.
2. Выполните разложение вашего года рождения на простые множители с последующей проверкой.
В системе MATLABпредусмотрены символьные операции, в частности, решение линейных и нелинейных уравнений. Рассмотрим некоторые примеры.
| >> syms x >> y = x^2 + 3*x + 1 y = x^2 + 3*x + 1 >> whos y Name Size Bytes Class Attributes y 1x1 112 sym >> x12 = solve(y) x12 = - 5^(1/2)/2 - 3/2 5^(1/2)/2 - 3/2 >> xx = double(x12) xx = -2.6180 -0.3820 >> x = xx(1) x = -2.6180 >> yd = subs(y) yd = >> x = xx(2) x = -0.3820 >> yd2 = subs(y) yd2 = |
Функция solve может быть использована и для выражения, заключенного в одинарные кавычки, например,
>> str = '3*p^2 + 5*p + 2'
str =
3*p^2 + 5*p + 2
>> whos str
Name Size Bytes Class Attributes
Str 1x15 30 char
>> q = solve(str)
q =
-1
-2/3
>> whos q
|
|
|


