Методы моделирования. Их использование в среде ИППП

В порядке повышения степени абстрагирования модели от реального объекта следуют физическое, аналоговое, статистическое, математическое моделирование. Из методов, косвенно поддерживающих проектирование, можно назвать имитационное, ситуационное, операционное моделирование. В разделе поискового проектирования будут рассмотрены модели представления инженерных знаний.

Физическая модель(макет) – это выполненная в натуральную величину или в масштабе копия объекта моделирования, сохраняющая только существенные черты его поведения. Например, модель для изучения аэродинамических свойств воспроизводит внешнюю (обтекаемую) поверхность. На стандартных осколочных макетах изучают закономерности дробления оболочек.

Преимущество макетирования в том, что изменение параметров макета вызывает отклик самой природы, а не, возможно неточной, теоретической модели. Эта информация незаменима для выявления закономерностей, но не для решения проектных задач непосредственно. Методом проб и ошибок пришлось бы перебрать слишком много макетов, чтобы найти удачное сочетание параметров. Цель физического моделирования другая: испытать достаточное количество параметрических вариантов макета, чтобы таблица результатов (рис. 5.1) могла служить источником информации о зависимости измеряемой величины y от параметров x ₁, …, x_n.

Аналоговая модель – это физическое устройство иной природы, чем моделируемый объект, но его поведение имеет точно такое же математическое описание. Аналоговый процесс должен быть управляемым, а параметры управления – пересчитываться на параметры реального процесса. Тогда результаты параметрического анализа аналогового процесса можно перенести на параметры и свойства проектируемого объекта. В качестве аналогового может быть выбран любой контролируемый процесс.

а	б
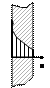
Рис. 5.2. Реальный (а) и аналоговый (б) процессы

При отработке ракетных двигателей применяют гидроинтегратор, моделиру­ю­щий распространение тепла другим процессом – течением вязкой жидкости (рис. 5.2). Оба процесса подчинены одним и тем же закономерностям: распространение тепла подчиняется линейному закону теплопроводности Фурье, поток вязкой жидкости связан такой же зависимостью со своим потенциалом – высотой z:

, ,

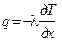где l – коэффициент теплопроводности, k – коэффициент гидравлического сопротивления. Процесс передачи тепла из камеры сгорания через стенку корпуса описывается уравнением теплопроводности, снижение уровня жидкости в цилиндрах z из-за гидравлического сопротивления связывающих их капилляров описывается аналогичным уравнением

, .

Математические модели реального и аналогового процессов идентичны. Изменение уровня жидкости можно наблюдать непосредственно, им можно управлять (подбирая капилляры и цилиндры с соответствующими сечениями, или изменяя вязкость жидкости), а параметры аналогового процесса можно пересчитать на параметры реального процесса по соотношению , где f _ц, f _к – площади сечения цилиндров и капилляров.

Преимущество аналогового моделирования – высокое быстродействие, позволяющее проводить многовариантный анализ, недостаток – невысокая точность. Погрешность измерения (уровня жидкости, тока на участке цепи), неконтролируемые флуктуации процесса, а также погрешности установления расчетных параметров процесса (сопротивление, емкость, вязкость) ограничивают достигаемую точность моделирования.

Статистические (регрессионные) модели получают обработкой результатов экспериментального исследования систем. Проблему идентификации модели F (x) математическая статистика рассматривает как задачу оценивания значения ненаблюдаемой случайной величины F по значению аргумента X = (x ₁, …, x_n).Наилучшая оценка 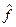(X) функции F (X) в смысле минимума квадрата ошибки

(5.5)

получается как условное математическое ожидание M [ F | X ] – регрессия случайной величины F на значениях X (рис. 5.3). Если зависимость 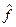(X) неизвестна или слишком сложна, приходится искать оценку регрессии в некотором ограниченном классе функций. Надежность восстановленной регрессии зависит от удачного выбора структуры уравнения регрессии, объема и качества статистического материала.

Заслуживают внимания методы прямого восстановления зависимости 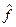(X) по экспериментальным данным, не требующие изначального определения ее математической структуры. Эти методы основаны на принципах самоорганизации – постепенного усложнения конкурирующих вариантов регрессионной модели с использованием фундаментальных механизмов естественного отбора (селекции, приспособления, обучения).

Математические модели сильно различаются по степени абстрагирования. В инженерных методиках используются физико-математические модели, построенные на эмпирически установленных закономерностях. Аэродинамическое сопротивление пропорционально квадрату скорости, закон сопротивления в плотных средах выражается квадратным трехчленом, коэффициенты которого регулируют соотношение динамической, инерционной и прочностной составляющих в разных диапазонах скоростей проникания. Во всех случаях коэффициенты согласуют результаты расчета с опытом, но имеют разный смысл. Коэффициент пропорциональности в формуле не зависит от формы тела согласно ударной теории Ньютона. В струйной теории, исправившей ошибку Ньютона, сопротивление подчиняется той же зависимости, но коэффициент пропорциональности, названный Эйлером коэффициентом сопротивления, характеризует обтекаемость тела. С пониманием аэродинамического сопротивления как равнодействующей давления среды на поверхности тела связаны коэффициенты подъемной силы, опрокидывающего момента, разложение полного аэродинамического сопротивления на характерные составляющие, условия полезности донных газогенераторов.

Таким образом, эмпирические коэффициенты в инженерных моделях играют двоякую роль. В структуре обобщенной модели они выражают влияние не учитываемых явно факторов и могут также служить согласующими параметрами для минимизации погрешности.

Комплекс математических моделей, способный адекватно воспроизводить реакцию системы на регулярные и случайные воздействия составляет имитационную модель системы. С помощью таких моделей имитируют поведение проектируемого объекта до изготовления опытного образца, чтобы изучить влияние случайных факторов, своевременно выявить и устранить дефекты конструкции, которые могли бы проявиться только на этапе натурных испытаний.

В интеллектуальной САПР для формирования имитационной модели используется технология, основанная на дуализме объектов: детерминированная объектная модель после оптимального согласования параметров усложняется (заменой присоединенных процедур) и формируется вероятностная модель объектов (назначением статуса «случайное» некоторым параметрам).

Дискретно-событийное моделирование использует механизм обмена сообщениями и реализуется как реакция объектов на сообщения (обнаружение цели, срабатывание заряда и т.п.). Естественным образом реализуется мультиагентное моделирование: индивидуальное поведение децентрализованных системных агентов, прикрепленных к каждому объекту, можно определить инструкциями или присоединенными процедурами. Благодаря этому статистическое моделирование в рамках сформированной вероятностной модели (с помощью интерфейса, часть которого показана на рис. 5.6) выполняется автоматически после указания необходимого числа испытаний.

Модель системной динамики математически представляет собой систему ОДУ, с которой легко справляется соответствующий решатель. Например, модель динамики боя (скорость убывания боевых единиц) может показать эффективность проектируемого БП во взаимодействии с другими видами оружия по критерию выигрыша боя в типовой ситуации. Пусть у каждой из двух сторон есть несколько позиций на расстояниях x_i от линии раздела, характеризуемых количеством m_i однородных боевых единиц, их скорострельностью l _i, вероятностью поражения боевой единицы противника на его s -й позиции. Относительные уменьшения численности боевых единиц на каждой позиции складываются из эффективных выстрелов со стороны нацеленных на нее (d _ki =1) позиций противника, что выражается системой:

(5.6)

С помощью графического интерфейса пользователь формирует позиции, определяет их характеристики, агент составляет систему (5.6) и решает ее. Самое сложное – определить матрицей d _ki, должна ли k -я позиция вести стрельбу по i -й позиции другой стороны для всех комбинаций индексов. Ситуация в каждой позиции характеризуется несколькими признаками (опасность позиций противника, эффективность стрельбы по ним, оставшееся количество единиц). Так как эти признаки меняются во времени (какие-то позиции подвижны), должно меняться и целераспределение, но как? Агент, закрепленный за каждой позицией, анализирует модель ситуации и выбирает решение, благоприятствующее наилучшей динамике боя для своей стороны.

Ситуационная модель – это из жизни роботов. Чтобы они могли ориентироваться на местности, заранее определяются классы возможных ситуаций и реакции на них. Системный агент тоже робот, он должен разбираться в ситуациях, возникающих в ходе работы, и лишь в крайних случаях обращать на них внимание пользователя. В интерактивной системе ситуационную модель можно развивать в режиме самообучения агента, если предварительно выделить классы ситуаций, научить агента идентифицировать их и формировать реакцию, принимая за образец действия пользователя.

Оценивать боевые возможности разрабатываемых БП необходимо для принятия правильных решений в вопросах, выходящих за рамки физического функционирования БП (какие типы снарядов должны входить в боекомплект танка, в какой пропорции, на какой спектр целей и условий применения оптимизировать проектируемый снаряд и т.п.). Для подготовки принятия решений разрабатывают модели типовых операций. Модель операции связывает имеющиеся у конфликтующих сторон стратегии (варианты действий) с достигаемым каждой стороной уровнем полезности. Формальное решение конфликтной ситуации методами исследования операций рекомендует оперирующей стороне целесообразную систему действий, придерживаясь которой, он гарантированно получит определенный результат, не зависящий от действий разумного противника (в рамках модели операции). Если его этот результат не устраивает, он должен улучшить свои стратегии, укрепить «слабое звено» (изменить состав боекомплекта, скорректировать критерии оптимальности и т.д.). Рассчитывать на гарантированный результат можно до тех пор, пока у противника не появится новая стратегия, то есть нужно следить за изменением моделей операций.