 |
Графоаналитический способ Верещагина вычисления интегралов в формуле Мора
|
|
|
|
А) б)
Рис. 13.1
Тогда, согласно  , имеем:
, имеем:
 (1)
(1)
Рассечём раму в стойке на расстоянии  . В поперечном сечении возникают внутренние силовые факторы
. В поперечном сечении возникают внутренние силовые факторы  (рис.13.1, а). От изменения (вариации) силы в точке
(рис.13.1, а). От изменения (вариации) силы в точке  в поперечном сечении рамы внутренние силовые факторы изменятся на бесконечно малые величины
в поперечном сечении рамы внутренние силовые факторы изменятся на бесконечно малые величины  Эти изменения внутренних сил и моментов будут пропорциональны
Эти изменения внутренних сил и моментов будут пропорциональны  , т.е.
, т.е.
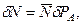


 ..... (2)
..... (2)
Из (2) следует, что при  коэффициенты
коэффициенты  ,
, 
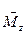 ,
,  являются нормальной силой, изгибающим моментом, крутящим моментом, перерезывающими силами в сечении рамы с координатой
являются нормальной силой, изгибающим моментом, крутящим моментом, перерезывающими силами в сечении рамы с координатой  , которые вызваны действием единичной силы в точке
, которые вызваны действием единичной силы в точке  в направлении
в направлении  искомого перемещения (рис. 13.2).
искомого перемещения (рис. 13.2).

А) б)
Рис. 13.2
Так как оператор вариации  имеет смысл дифференциала, то варьируя формулу потенциальной энергии
имеет смысл дифференциала, то варьируя формулу потенциальной энергии
 ,
,
получим:

Учитывая  , подставляя в
, подставляя в  и сокращая на
и сокращая на  , находим формулу
, находим формулу
 (3)
(3)
называемую формулой Мора. Она служит для определения любых обобщённых перемещений в стержневых системах.
Формулу Мора можно получить, пользуясь принципом возможных перемещений. Рассмотрим схему нагружения (см.рис. 13.2, а), когда в точке А в направлении искомого перемещения 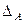 приложена единичная сила
приложена единичная сила  вызывающая в поперечном сечении системы внутренние силовые факторы
вызывающая в поперечном сечении системы внутренние силовые факторы  (рис. 13.2, б). Согласно принципу возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы
(рис. 13.2, б). Согласно принципу возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы 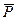 на возможном перемещении
на возможном перемещении 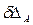 :
:

Выберем возможные перемещения пропорциональными действительным:

Тогда после подстановки получим:
 (4)
(4)
Если учесть, что

то приходим к формуле (3).
Для систем, элементы которых работают на растяжение или сжатие (например, шарнирно-стержневые системы - фермы), в формуле Мора (3) отличен от нуля будет только слагаемое, содержащее продольные силы. При расчете балок или рамных систем, работающих в основном на изгиб, влияние поперечной и продольной силы на перемещение несущественно и в большинстве случаев их влияние не учитывается. В случае пространственной работы стержня или стержневой системы, элементы которой работают, в основном, на изгиб и кручение, в формуле Мора обычно ограничиваются рассмотрением слагаемых, содержащих изгибающие и крутящие моменты.
|
|
|
Подробно рассмотрим случай, когда брус работает только на изгиб (Mx  0, Nz = Mz = My = Qx = Qy = 0). В этой ситуации выражение (3) принимает вид:
0, Nz = Mz = My = Qx = Qy = 0). В этой ситуации выражение (3) принимает вид:
 (5)
(5)
Согласно (5) для определения перемещения произвольной точки в произвольном направлении, последовательно необходимо выполнять следующее:
1. Построить эпюру моментов Мx от заданной системы внешних сил;
2. Исключая внешние силы и в точке, где необходимо определить перемещение по заданному направлению, прикладывается единичное усилие (сосредоточенная сила - если требуется определить линейное перемещение; сосредоточенный момент - если требуется определить угловое перемещение), и от действия единичного усилия строится эпюра моментов  ;
;
3. По формуле Мора (5) вычисляется искомое перемещение.
Полученный по формуле Мора положительный знак перемещения показывает, что искомое перемещение происходит по направлению, совпадающему с принятым направлением единичной обобщенной силы, отрицательный знак перемещения говорит о том, что точки оси перемещаются (сечения поворачиваются) в сторону, противоположную направлению единичной обобщенной силы.
Формулы Мора пригодны и для элементов, представляющих собой стержни малой кривизны, с заменой элемента длины  в подынтегральном выражении элементом дуги
в подынтегральном выражении элементом дуги  .
.
Примеры определения перемещений с помощью формулы Мора
Пример 1.
|
|
|
Пусть требуется в простейшей ферме (рис. 13.3) определить вертикальное и горизонтальное перемещение узла А.

А) б) в)
Рис. 13.3
Усилия в стержнях фермы 
Формула Мора (3) имеет вид:
 (6)
(6)
Усилия 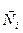 найдём из рис.13.3, б,в. При определении вертикального перемещения единичную силу приложим к узлу А в вертикальном направлении (рис. 13.3, б). Усилия
найдём из рис.13.3, б,в. При определении вертикального перемещения единичную силу приложим к узлу А в вертикальном направлении (рис. 13.3, б). Усилия  Согласно (6) получаем:
Согласно (6) получаем:

При определении горизонтального перемещения единичную силу прикладываем к узлу  в горизонтальном направлении (рис. 7.9,в). Усилия от единичной силы
в горизонтальном направлении (рис. 7.9,в). Усилия от единичной силы  Следовательно,
Следовательно,

Пример 2.
Пусть требуется определить вертикальное перемещение и угловое перемещение в точке  балки (рис. 13.4).
балки (рис. 13.4).
Для определения перемещений воспользуемся формулой Мора для обобщённых перемещений:
 (7)
(7)

Рис. 13.4
Из рис. 13.4 находим  Найдём сначала вертикальное перемещение точки А. Приложим к балке в точке А в вертикальном направлении единичную силу
Найдём сначала вертикальное перемещение точки А. Приложим к балке в точке А в вертикальном направлении единичную силу  (рис. 13.5, а). Находим момент
(рис. 13.5, а). Находим момент  Подставляя значения моментов в формулу Мора (7), находим:
Подставляя значения моментов в формулу Мора (7), находим:


А) б)
Рис. 13.5
Знак плюс указывает на то, что перемещение произошло в том направлении, в котором действует единичная сила.
Найдём теперь угловое перемещение поперечного сечения в точке  . Приложим в точке
. Приложим в точке  единичный момент (рис. 13.5, б) и определим
единичный момент (рис. 13.5, б) и определим  Подставляя значения моментов в (7), получим:
Подставляя значения моментов в (7), получим:

Поворот сечения произошёл в том же направлении, в каком производит вращение единичный момент.
Пример 3.
Пусть требуется определить вертикальное и горизонтальное перемещение точки  в кривом стержне (рис. 13.6, а) постоянного радиуса кривизны
в кривом стержне (рис. 13.6, а) постоянного радиуса кривизны 
Для определения перемещений воспользуемся формулой Мора в виде (7), пренебрегая влиянием нормальной 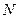 и перерезывающей
и перерезывающей  сил. Изгибающий момент в произвольном сечении, определяемом углом
сил. Изгибающий момент в произвольном сечении, определяемом углом 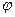 (рис. 13.6, б), равен
(рис. 13.6, б), равен 
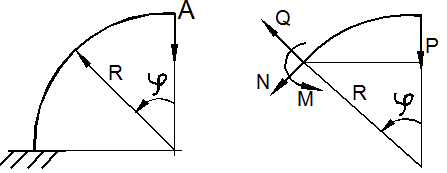
А) б)
Рис. 13.6

А) б)
Рис. 13.7
Для определения вертикального и горизонтального перемещений соответственно имеем (рис. 13.7).  Подставляя выражения моментов в формулу Мора в форме (7), получим:
Подставляя выражения моментов в формулу Мора в форме (7), получим:

В рассмотренном примере считается, что размеры поперечного сечения малы по сравнению с радиусом  Это предположение позволяет использовать формулу Мора, полученную для прямого бруса, применительно к кривому брусу.
Это предположение позволяет использовать формулу Мора, полученную для прямого бруса, применительно к кривому брусу.
|
|
|
Пример 4.
Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.13.8, а), методом Мора.
Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов  (рис.13.8, б). Второе состояние (единичное) – при действии сосредоточенной силы
(рис.13.8, б). Второе состояние (единичное) – при действии сосредоточенной силы  , приложенной в точке С; ему соответствует эпюра моментов
, приложенной в точке С; ему соответствует эпюра моментов  (рис.13.8, в). Третье состояние (также единичное) – при действии сосредоточенного момента
(рис.13.8, в). Третье состояние (также единичное) – при действии сосредоточенного момента  , приложенного в точке В; ему соответствует эпюра моментов
, приложенного в точке В; ему соответствует эпюра моментов  (рис.13.8, г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:
(рис.13.8, г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:

Вычисляем прогиб балки в точке С:

Знак "+" означает, что точка С переместится в направлении действия силы. 
Вычисляем угол поворота сечения В:

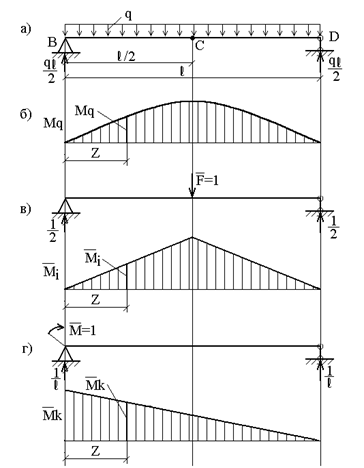
Рис. 13.8
Знак "+" означает, что сечение В поворачивается в направлении действия момента  то есть по часовой стрелке.
то есть по часовой стрелке.
Пример 5.
Определить прогиб балки в середине пролета (рис.13.9, а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба.

Рис. 13.9
Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.13.9, а); ему соответствует эпюры изгибающих моментов  (рис.13.9, б) и поперечных сил
(рис.13.9, б) и поперечных сил  (рис.13.9, в).
(рис.13.9, в).
Второе состояние (единичное) – при действии силы  (рис.13.9, г); ему соответствуют эпюры изгибающих моментов
(рис.13.9, г); ему соответствуют эпюры изгибающих моментов 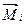 (рис.13.9, д) и поперечных сил
(рис.13.9, д) и поперечных сил  (рис.13.9, е).
(рис.13.9, е).
В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (3) принимает вид:

Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.13.9) для составляющих полного перемещения получим:

Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами  и
и  , при этом
, при этом  .
.
Тогда площадь сечения и его осевой момент инерции равны:


Будем считать, что 
 тогда:
тогда:

то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения  влияние поперечных сил на величину прогиба становится еще менее значительным.
влияние поперечных сил на величину прогиба становится еще менее значительным.
|
|
|
Графоаналитический способ Верещагина вычисления интегралов в формуле Мора
Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формулы (3, в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.
Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина, который предложил студент МИИЖТ Верещагин в 1924 году и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.
Докажем справедливость этого правила.
Интегралы Мора с точностью до постоянного множителя представляют собой интегралы от произведения двух функций вида:

где, по крайней мере, одна из функций (рис. 13.10)

является линейной ( - постоянные величины).
- постоянные величины).
Возьмём к примеру, интеграл
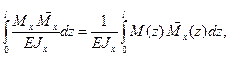
где  - момент от единичной обобщённой силы – линейная функция,
- момент от единичной обобщённой силы – линейная функция,  - в общем случае – криволинейная функция.
- в общем случае – криволинейная функция.
Подставляя выражение для  в выражение для
в выражение для 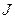 и производя почленное интегрирование, найдём:
и производя почленное интегрирование, найдём:
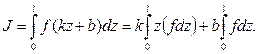

Рис. 13.10
Из рис. 13.10 следует, что  есть элементарная площадь криволинейной эпюры,
есть элементарная площадь криволинейной эпюры,  - статический момент этой элементарной площади относительно оси
- статический момент этой элементарной площади относительно оси  .
.
Поэтому:
 (8)
(8)
Из полученной формулы (8) следует простое правило вычисления интегралов Мора: интеграл с точностью до постоянного множителя равен произведению площади  криволинейной эпюры
криволинейной эпюры  на ординату
на ординату  взятую из прямолинейной эпюры под центром тяжести криволинейной эпюры.
взятую из прямолинейной эпюры под центром тяжести криволинейной эпюры.
На первый взгляд, описанный графоаналитический способ вычисления интегралов Мора не даёт упрощений, т.к. всё равно приходится вычислять площадь  криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простейших – прямоугольник, треугольник, симметричную квадратичную параболу и др. Эти эпюры приведены на рис. 13.11.
криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простейших – прямоугольник, треугольник, симметричную квадратичную параболу и др. Эти эпюры приведены на рис. 13.11.
|
|
|

А) б) в) г)
Рис. 13.11
В первом случае  во втором
во втором  в третьем
в третьем 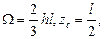 в четвёртом
в четвёртом 
Рассмотрим несколько сложных эпюр (рис. 13.12): а) эпюра разбивается на симметричную параболу, треугольник и прямоугольник; б) эпюра пересекает ось стержня, её можно дополнить сверху и снизу равными площадями и разложить на два треугольника, доказательство добавляемых площадей элементарно: из подобия заштрихованных треугольников следует  откуда
откуда  что и доказывает утверждение;
что и доказывает утверждение;
в) эпюра разбивается на симметричную параболу и два треугольника, соответствующих случаю (б).

А) б) в)
Рис. 13.12
Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра является прямолинейной.
Применение готовых формул показано в таблице 13.1. Сами эти формулы без труда определяются элементарными методами. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпюрам, а также криволинейной с прямолинейной. Если любая из фигур, приведенных в табл. 13.1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что Мa = Мb .
При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в таблице 13.1.
Таблица 13.1
| M 2(x) M 1(x) | 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 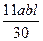
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|
Примеры вычисления перемещений способом Верещагина
Пример 6.
Определим вертикальное перемещение точки  консольной балки (рис. 13.13, а) по формуле Мора (3) с использованием способа Верещагина.
консольной балки (рис. 13.13, а) по формуле Мора (3) с использованием способа Верещагина.

А) б)
Рис. 13.13
С этой целью строим эпюру моментов от заданной нагрузки  (рис. 13.13, б). Эпюру от заданной нагрузки разбиваем на две простейшие – треугольник и симметричную параболу. В результате имеем:
(рис. 13.13, б). Эпюру от заданной нагрузки разбиваем на две простейшие – треугольник и симметричную параболу. В результате имеем:

или

При перемножении площади  эпюры от внешней нагрузки на ординату
эпюры от внешней нагрузки на ординату  эпюры от единичной нагрузки следует руководствоваться правилом: если эпюры лежат по одну сторону от оси балки, то они одного знака и потому дают знак плюс. В противном случае – знак минус.
эпюры от единичной нагрузки следует руководствоваться правилом: если эпюры лежат по одну сторону от оси балки, то они одного знака и потому дают знак плюс. В противном случае – знак минус.
Пример 7.
Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.13.14, а), способом Верещагина.
Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра Mq (рис.13.14, б), и два единичных состояния - при действии силы  приложенной в точке С (эпюра
приложенной в точке С (эпюра  , рис.13.14, в), и момента
, рис.13.14, в), и момента  , приложенного в точке В (эпюра
, приложенного в точке В (эпюра  , рис.13.14, г).
, рис.13.14, г).
Прогиб балки в середине пролета:
 .
.
Аналогичный результат был получен ранее методом Мора (см. пример 4). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры  умножить на расположенную под ее центром тяжести ординату эпюры
умножить на расположенную под ее центром тяжести ординату эпюры  (
( на рис.13.14, в), то величина перемещения будет совершенно иной и неправильной так как эпюра
на рис.13.14, в), то величина перемещения будет совершенно иной и неправильной так как эпюра  ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.
ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.
А при вычислении угла поворота сечения в точке В можно площадь эпюры  умножить на расположенную под ее центром тяжести ординату эпюры
умножить на расположенную под ее центром тяжести ординату эпюры  (
( , рис.13.14, г), так как эпюра
, рис.13.14, г), так как эпюра  ограничена прямой линией:
ограничена прямой линией:
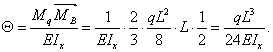
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 4).

Рис. 13.14
Пример 8.
Найдём взаимное сближение точек А и В рамы (рис. 13.15, а), т.е.  , используя формулу Мора и способ Верещагина.
, используя формулу Мора и способ Верещагина.

А) б)
Рис. 13.15
На рис. 7.18, а и б построены эпюры моментов от внешней силы  и обобщённой единичной силы
и обобщённой единичной силы  , где
, где  Искомое взаимное перемещение
Искомое взаимное перемещение
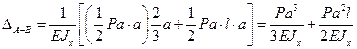 .
.
Пример 9.
Найдём вертикальное перемещение точки пространственной рамы (рис. 13.16, а) по формуле Мора (3):

которая учитывает кручение и изгиб стержней рамы. На рис. 13.16 приведены эпюры изгибающих моментов от заданной и единичной нагрузок.
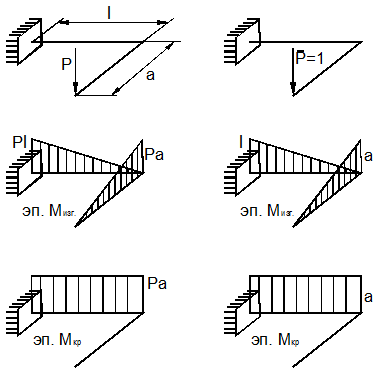
А) б)
Рис. 13.16
Вычисление даёт:

Определение температурных перемещений в балках и рамах
Перемещение в балках могут вызываться не только силами, но и изменениями температуры. Если по высоте сечения температура изменилась на  градусов равномерно, то брус испытает удлинение на каждом участке
градусов равномерно, то брус испытает удлинение на каждом участке  , равное:
, равное:
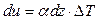 ,
,
где  - коэффициент линейного температурного расширения, и тогда, согласно формуле (4):
- коэффициент линейного температурного расширения, и тогда, согласно формуле (4):

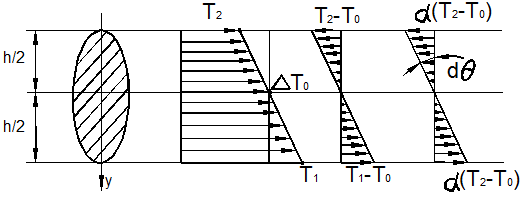
Эпюра Т Эпюра  Эпюра
Эпюра 
Рис. 13.17
Если температура изменяется по высоте балки по линейному закону (рис.13.17), то удлинение крайних волокон:


откуда угол поворота сечения:
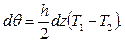
Тогда, согласно (4):

При одновременном эффекте имеем:
 (9)
(9)
Пример 10.
Определим вертикальное перемещение точки  консольной балки, у которой нижняя сторона имеет температуру
консольной балки, у которой нижняя сторона имеет температуру  , а верхняя -
, а верхняя -  <
<  (рис. 13.18, а).
(рис. 13.18, а).

А) б)
Рис. 13.18
В данной задаче  определяется линейной эпюрой, изображённой на рис. 13.18, б.
определяется линейной эпюрой, изображённой на рис. 13.18, б.
Поэтому на основании (9) получаем:


|
|
|


