 |
Оптимум потребителя (кардиналистский и ординалистский подходы).
|
|
|
|
 В соответствии с кардиналистской теорией полезности, индивид стремится максимизировать полезность, и потребительское равновесие достигается, когда предельная полезность последней денежной единицы, потраченной потребителем на тот или иной товар, является в точности такой же, как и предельная полезность последней денежной единицы, потраченной потребителем на любой другой товар.
В соответствии с кардиналистской теорией полезности, индивид стремится максимизировать полезность, и потребительское равновесие достигается, когда предельная полезность последней денежной единицы, потраченной потребителем на тот или иной товар, является в точности такой же, как и предельная полезность последней денежной единицы, потраченной потребителем на любой другой товар.
Ординалистская теория полезности отрицает возможность сопоставления полезности, поэтому оптимум (равновесие) потребителя находится здесь путем совмещения карты безразличия и бюджетной линии.
Для максимизирующего полезность индивида товарные наборы, находящиеся на тех кривых безразличия, которые более удалены от начала координат карты безразличия, предпочтительнее наборов на менее удаленных кривых. Например, на рис. 30 точка А предпочтительнее для потребителя, чем точки В и Е. Однако товарный набор, которому соответствует точка А, недоступен потребителю, так как в своем стремлении к максимальному удовлетворению он встречается с описываемыми бюджетной линией ограничениями.
Следовательно, равновесие потребителя установится в той точке, т. е. при таком наборе товаров, когда достигается наибольший возможный уровень полезности при данном бюджетном ограничении. Потребитель, например, не выберет точку В на рис. 30, в которой бюджетная линия пересекает кривую безразличия I, так как, двигаясь вверх по бюджетной линии, он может перейти к товарным наборам, лежащим на более привлекательных кривых безразличия. Наивысшей доступной для потребителя кривой безразличия является кривая II, соприкасающаяся с бюджетной линией в точке Е. Поскольку в этой точке линия бюджетного ограничения является касательной к кривой безразличия, то наклон бюджетной линии равен наклону кривой безразличия. Иначе говоря, относительная цена двух товаров равна их предельной норме замещения. Поэтому равновесие потребителя может быть записано при помощи следующей формулы:
|
|
|
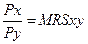
Таким образом, товарный набор, в котором предельная норма замещения двух товаров равна их относительной цене, т. е. бюджетная линия и кривая безразличия соприкасаются, оптимален для потребителя.
p.s. Кривые безразличия, бюджетная линия
Кривая безразличия – это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. На рис. Товарный набор А включает Xa единиц товара X и Ya едениц товара У. Если, с точки зрения потребителя, наборы А и B равноценны, то точки А и B лежат на одной и той же кривой безразличия. Кривая безразличия отражает предпочтения потребителя к тому или иному товару и готовность купить больше товара А за место какого-либо количества товара В. А бюджетная линия показывает возможности, бюджет покупателя. При совмещении этих двух графиков мы получаем наиболее оптимальный вариант для потребителя в точке их касания. Бюджетная линия зависит как от дохода потребителя, так и от цен на блага.
Кривые безразличия обладают следующими свойствами:
1.Имеют отрицательный наклон
2.Абсолютная величина наклона в любой точке есть отношение предельной полезности блага, отсчитывая по горизонтальной оси, к предельной полезности, отсчитывая по вертикальной оси.
3.Кривые безразличия не пересекаются
4.Кривые безразличия выпуклы
5.Можно построить кривую безразличия, проходящую через любую корзину товаров.
КРИВАЯ БЕЗРАЗЛИЧИЯ
При порядковом подходе используется кривые и карта безразличия. Кривая безразличия - это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично какой из этих наборов выбрать. Если заполнить двухмерную плоскость кривыми безразличия так плотно, как это возможно, получим карту безразличия.
|
|
|
На рисунке 1 товарный набор А включает ХА единиц товара Х и УА единиц товара У, товарный набор В включает ХВ единиц товара Х и УВ единиц товара У. Если точки зрения данного потребителя набора А и В равноценны то точки А и В лежат на одной и той же кривой безразличия
|
|
|


