 |
Сложение и вычитание обыкновенных дробей
|
|
|
|
1. Сложение и вычитание дробей с одинаковыми знаменателями.
Исследование, проведенное Алышевой Т.В.1, свидетельствует о целесообразности при изучении действий сложения и вычитания обыкновенных дробей с одинаковыми знаменателями использовать аналогию со сложением и вычитанием уже известных учащимся
Алышева Т. В. Изучение арифметических действий с обыкновенными дробями учащимися вспомогательной школы //Дефектология. —1992.— № 4.— С. 25-27.
исел, полученных в результате измерения величин, и проводить ручение действий дедуктивным методом, т. е. «от общего к частому».
Сначала повторяется сложение и вычитание чисел с наимено-»аниями мер стоимости, длины. Например, 8 р. 20 к. ± 4 р. 15 к.
Лри выполнении устного сложения и вычитания нужно склады-
1ать (вычитать) сначала рубли, а потом копейки.
3 м 45 см ± 2 м 24 см — сначала складываются (вычитаются) метры, а потом сантиметры.
; При сложении и вычитании дробей рассматривается общий случай: выполнение этих действий со смешанными дробями (знаменатели одинаковые): 3-?- ± 1-г. В этом случае надо: «Сложить (вычесть) целые числа, затем числители, а знаменатель остается тем же». Это общее правило распространяется на все случаи сложения и вычитания дробей. Постепенно вводятся частные случаи: сложение смешанного числа с дробью 1у + -=•= \-= \, потом
(1 1\ ^ '
смешанного числа с целым \-= + 4 = 5у. После этого рассматриваются более трудные случаи вычитания: 1) из смешанного числа дроби: 4д~п=4д-; 2) из смешанного числа целого: 4д—2=2-д-.
После усвоения этих достаточно простых случаев вычитания учащиеся знакомятся с более трудными случаями, когда требуется преобразование уменьшаемого: вычитание из одной целой единицы или из нескольких единиц, например:
|
|
|
\ О О О 2, л О <-)Э О п~
1~Ь-~Ь~Ь-~5' 6~~5~2Ь~'5-2'5-
В первом случае единицу нужно представить в виде дроби со знаменателем, равным знаменателю вычитаемого. Во втором случае из целого числа берем единицу и также ее записываем в виде неправильной дроби со знаменателем вычитаемого, получаем в уменьшаемом смешанное число. Вычитание выполняется по общему правилу.
Наконец рассматривается наиболее трудный случай вычитания: из смешанного числа, причем числитель дробной части меньше
1 3
числителя в вычитаемом: 5^— ^. В этом случае надо уменьшаемое изменить так, чтобы можно было применить общее правило, т. е. в уменьшаемом занять из целого одну единицу и раздробить
.5 1 6
в пятые доли, получим 1=-г, да еще -г, получится -г, прим<-|>
,6 3 5 5 &
примет такой вид: 4^~ ^, к его решению уже можно применим
общее правило.
Использование дедуктивного метода обучения сложению и вычп танию дробей будет способствовать развитию у учащихся умении обобщать, сравнивать, дифференцировать, включать отдельные случаи вычислений в общую систему знаний о действиях с дробями.
2. Сложение и вычитание дробей и смешанных чисел с разными знаменателями*.
а) больший знаменатель является НОЗ:
о?+|, Н; 2) 1|+', 4-ш' 3> 4+4 4-4
б) больший знаменатель не является НОЗ:
п 3 4 7 2. 9г.3, 7,3 2. 04^2.. 1 гЗ 92 1} Б-+7' 8-9' 2) %+8' 15—5' 3) %+%' 5Т-23'
Выполнение сложения и вычитания дробей, имеющих разные з менатели, представляет значительные трудности для умственно -сталых школьников, так как, прежде чем выполнять действия, требуется привести дроби к наименьшему знаменателю, в связи с чем внимание учащихся переключается на дополнительную операцию (удлиняется запись выражения — требуется несколько раз переписывать выражение, ставя знак равенства). Это требует от учащихся сосредоточенности внимания. А внимание учащихся с нарушением интеллекта характеризуется, как известно, отвлекаемостью, рассеянностью. Это нередко приводит к потере целых, знака равенства, а то и компонента. Чтобы избежать подобных ошибок, можно на первых порах предложить учащимся запись выражения проговорить устно, а именно сказать, какие операции надо выполнить и в какой последовательности: 1) привести дроби к наименьшему знаменателю; 2) выполнить действие; 3) произвести, если нужно, преобразование в ответе.
|
|
|
При выполнении сложения дроби со смешанным числом надо обратить внимание учащихся на значение суммы и каждого слагаемого, сравнив со свойством суммы целых чисел.
То же самое необходимо сделать и при знакомстве с вычитанием дробей, подчеркнув общность свойств разности целых и дробных чисел.
Для этого целесообразно решить и сравнить пары примеров на нахождение суммы и разности целых и дробных чисел: 310
396+127
4,3. 3, -1 5 + 5' 1ТО+5ТО
Вывод: сумма больше каждого из слагаемых, разность меньше или равна уменьшаемому.
Сложение и вычитание дробей необходимо связать с жизненно-практическими заданиями и упражнениями, которые могут быть мыполнены и устно. Например:
«На отделку блузки отрезали -^ м белой и -^ м синей тесьмы.
Сколько тесьмы пошло на отделку блузки?»
ъ - - о -3
«От рейки длиной 2 м отпилили один кусок длиной -% м и
„ 1,, - ->
второй — длиной 4" м. Какова длина оставшейся рейки?»
Отметим, что в этих задачах даны числа, полученные от измерения величин. Это позволяет закрепить в памяти учащихся наиболее употребительные в повседневной жизни соотношения: •к- м — это 50 см, -^ м — это 25 см, -? м — это 20 см, -^ ч — это 15 мин и т. д.
В этот период следует решать с учащимися примеры на нахождение неизвестных компонентов сложения и вычитания, сопоставляя нахождение неизвестных компонентов сложения и вычитания дробных и целых чисел.
Учащиеся должны убедиться, что переместительный и сочетательный закон арифметических действий над целыми числами распространяются и на действия над дробными числами. Так же как и при изучении действий с целыми числами, учащиеся получают
лишь практическое знакомство с законами — их использование
3 для рационализации вычислений. Например, решить пример -^+2
|
|
|
удобнее, переставив местами слагаемые, т. е. использовав переместительный закон сложения.
Решение примеров с предварительным обдумыванием порядка выполнения действий развивает сообразительность, смекалку, предупреждает шаблонность и имеет большое корригирующее значение.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ*
В школе VIII вида рассматривается только умножение и деление дробей и смешанных чисел на целое число. Изучение этих
действий, так же как и изучение сложения и вычитания, дает параллельно.
Для удобства изложения мы сначала рассмотрим методику зь
комства с умножением дроби на целое число, а затем с деление
дроби на целое число. •
Прежде чем знакомить учащихся с умножением дроби на цел^ число, необходимо повторить умножение целых чисел.
При рассмотрении умножения дроби на целое число необхоД| мо соблюдать определенную последовательность разных случае] которая определяется степенью их трудности.
1.Умножение дроби на целое число.
2. Умножение смешанного числа на целое.
Подготовительными заданиями к объяснению умножения дрой
на целое число являются задания на умножение целых чисел | последующей заменой действия умножения действием сложений например: заменить умножение 7-3=21 сложением 7+7+7=21| заменить действие умножения (первый множитель — дробь второй множитель — целое число) действием сложен» д-хЗ=д-+д-4-д-=-д. При этом обращается внимание на числитель знаменатель произведения и первого множителя. С помощью во просов: «Изменился ли знаменатель дроби при умножении? Чт| произошло с числителем дроби?» — учащиеся приходят к выводу^ что числитель увеличился в 3 раза, а знаменатель не изменился.. Для вывода правила умножения дроби на целое число недостаточно ограничиться рассмотрением только одного примера, нужно, рассмотреть еще несколько примеров:
| 2 7 * - |
| 2,2,2 2+2+2 =++7=~7~ |
2 • 3 6
- ~-7;
| 3,3 |
3 • 2 6 3 ~
Правильность ответов в этих примерах необходимо подтвердить демонстрацией рисунков.
В рассмотренных примерах внимание учащихся надо обратить на то, что в числителе сумму одинаковых слагаемых (трех двоек) можно заменить произведением (2 • 3). Это позволит подвести их
|
|
|
л » 2 о 2 • 3 6
к более сокращенной записи: у 3= — ^ — =у, а следовательно, и к
выводу правила. Кроме того, при умножении дроби на целое число получается произведение, большее первого множителя. После усвоения правила умножения дроби на целое число необходимо показать учащимся, что до умножения числителя на целое 312
Исло надо сопоставить эти числа со знаменателем и, если у них Ьть общий делитель, разделить на него и только потом произвес-умножение. Такой прием предварительного сокращения чисел,
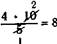
|
| 10 = |
| Е |
писанных в числителе и знаменателе, облегчает вычисления, пример: -г-10=—?—=-г-=8. Это же действие выполним с пред-рительным сокращением числителя и знаменателя на общий |делитель:
I Дети с интеллектуальным недоразвитием редко прибегают к | рациональным приемам вычисления, используя, как правило, только те приемы, которые стали стереотипными. Поэтому учителю надо иногда просто требовать, чтобы учащиеся использовали рациональные способы действий.
Перед объяснением умножения смешанного числа на целое необходимо повторить умножение чисел, полученных при измерении величин, вида 15 р. 32 к.-3. Сначала следует дать подробную запись при решении этого примера: 1 р. = 100 к.
1532 к.
15 р. = 100 к.-15=1500 к. 1500 к.+32 к. = 1532 к.
4596 к.
Однако тут же надо показать, что некоторые примеры легче решать в уме, умножая отдельно число рублей и копеек.
При умножении смешанного числа на целое обращается внимание на то, что смешанное число надо выразить (записать) в виде неправильной дроби, а затем выполнять умножение по правилу умножения дроби на целое число, например:
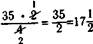
|
-4 _ 35 „
(Сопоставить с умножением 15 р. 32 к. на целое число 3.)
Недостатком этого способа вычислений является его громоздкость: большие числа, которые получаются в числителе, затрудняют вычисления. Однако у этого способа есть и преимущество: в дальнейшем, когда учащиеся будут знакомиться с делением смешанного числа на целое, перед выполнением действия им потребуется выразить смешанное число неправильной дробью.
Наиболее сильным учащимся можно показать и второй сп| умножения смешанного числа на целое (без записи смешан| числа неправильной дробью), например:

|
(Сопоставить с умножением чисел, полученных от измерения личин, устно: 15 р. 32 к. -3=45 р. 96 к.)
В этом случае умножается целое число на целое, получен», произведение записывается целым числом, затем умножаете!, дробная часть числа по правилу умножения дроби на целое число,.
При изучении темы «Умножение дроби на целое число» следу*! ет решать примеры и задачи на увеличение дроби в несколько!
|
|
|
2 раз. Необходимо показать учащимся, что пример у 3 можно про*
2 2 I
читать по-разному: у умножить на 3, у увеличить в 3 раза, найти!
22 I
произведение у и 3; множители у и 3, найти произведение. После!
2 о 6 '
решения примера уЗ=у следует сравнить произведение и пер-
6 ' 2 ~ 2 6 0
выи множитель: у больше у в 3 раза, •=• меньше у в 3 раза.
Надо решать примеры и с неизвестным числителем или знаменателем в первом множителе вида: -~--2=-г, т=г-2=-я-.
Можно предложить и более трудные примеры вида:
. а, 4 1,-, 3 П г-, 2
1-а-4=Ъи'а=Г> П'П=5
2. Дробь тг увеличить в 3 раза.
Деление дроби на целое число дается в следующей последовательности:
1.Деление дроби на целое число без предварительного сокра
щения.
2. Деление смешанного числа на целое число без предваритель
ного сокращения.
3. Деление с предварительным сокращением.
Учащимся необходимо показать и такие случаи деления дроби или смешанного числа на целое, когда предварительное сокращение облегчает процесс выполнения действия. Например:
4Ж2 315Ш5
5-2=7^-=5' 34-9 = Т":9 = 4^=Т2-
1 3
На основе наблюдений и конкретной деятельности учащиеся
н'мнодятся к выводу: при делении дроби на целое число доли
1.ПЮВЯТСЯ мельче, число же долей не изменяется. Например,
| гни взять половину яблока и разделить эту половину на 2 рав-
ц.к' части (-я-: 2 ], то получится по -т яблока. Записываем: -к\2=-^.
Каждый ученик должен самостоятельно половину круга (полоски, Отрезки) разделить на 2 равные части и записать результат деле-
ния.
Далее рассматривается деление, например, -^ на 3 равные
2 2
Части: -^:3=к- Учащиеся видят, что получились при делении девятые доли, а число их не изменилось. Сравниваются числитель и знаменатель частного и делимого: знаменатель увеличился в 3 раза, а числитель не изменился. Отсюда можно сделать вывод: чтобы разделить дробь на целое число, нужно знаменатель умножить на это число, а числитель оставить тот же. На основе правила решается пример:  Затем на предметах уча-
Затем на предметах уча-
щиеся должны еще раз показать процесс деления и убедиться, что пример решен верно.
Деление дроби на целое число необходимо сопоставить с умножением дроби на целое число, решая взаимно обратные примеры вида 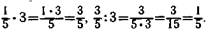 При этом следует сравнить
При этом следует сравнить
произведение и частное соответственно с первым множителем и делимым. Это надо для того, чтобы учащихся подвести к обобщению: при умножении дроби на целое число произведение во столько раз больше первого множителя, сколько единиц содержится во втором множителе. Аналогичный вывод нужно сделать и для частного.
Деление смешанного числа на целое дается по аналогии со вторым способом умножения смешанного числа на целое, например: 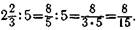 Смешанное число обращается в непра-
Смешанное число обращается в непра-
вильную дробь и деление производится по правилу деления дроби на целое число.
Наиболее сильных учащихся нужно познакомить и с особыми случаями деления. Если целая часть смешанного числа нацело делится на делитель, то смешанное число не обращается в непра-
вильную дробь, например: 2-^'.2=\-^. Нужно делить сначала
часть, результат записать в частное, затем делить дробную част
2 22
правилу деления дроби на целое число: 12^:3=47^=4-^. В
случае деление смешанного числа нужно показать на предметиц пособиях. После изучения всех четырех действий с обыкновений ми дробями предлагаются сложные примеры со скобками и порядок действий.
|
|
|


