 |
Задача №1. Решить графическим методом типовую задачу оптимизации
|
|
|
|
Владикавказский филиал Финуниверситета
Кафедра «Математика и информатика»
Музаев И.Д.
Методы оптимальных решений
Методические рекомендации по выполнению контрольной работы
для студентов, обучающихся по направлению
38.03.01 Экономика (очная форма обучения)
Квалификация (степень бакалавр)
Рассмотрено и одобрено на заседании
кафедры «Математика и информатика»
протокол ___ от ______________ 2017 г.
Зав.кафедрой ____________Казарян М.Л.
Владикавказ 2017
Содержание
1. Перечень вопросов для самоконтроля студентов
по дисциплине «Методы оптимальных решений»………………………….. 3
2. Образцы решения задач…………………………………………………....6
3. Задания к контрольной работе……………………………………………..16
Перечень вопросов для самоконтроля студентов
По дисциплине «Методы оптимальных решений»
1. Основные этапы принятия оптимальных решений.
2. Общая постановка и классификация задач оптимизации.
3. Примеры задач линейного программирования в экономике.
4. Постановка и формы записи задачи ЛП.
5. Геометрическая интерпретация задачи ЛП (постановка задачи, алгоритм решения, пример).
6. Симплекс метод (алгоритм метода, пример)
7. Метод искусственного базиса (алгоритм выбора начального базиса, пример).
8. Двойственные задачи ЛП (определения, пример).
9. Основное неравенство теории двойственности. Теорема о существовании прямого и двойственного решений, теорема о дополняющей нежесткости. Примеры использования теорем двойственности для построения оптимального решения задачи ЛП.
10. Экономическая интерпретация двойственной задачи. Третья теорема двойственности (об оценках). Пример использования объективно обусловленных оценок для принятия оптимальных решений.
|
|
|
11. Транспортная задача. Общая постановка. Открытая и закрытая ТЗ.
12. Метод северо-западного угла (алгоритм метода, пример).
13. Метод наименьшей стоимости (алгоритм метода, пример).
14. Определение первоначального распределения поставок в вырожденном случае, когда из рассмотрения выпадают одновременно и строка и столбец.
15. Проверка оптимальности базисного распределения поставок (определения, примеры).
16. Улучшение неоптимального плана перевозок (определение цикла перераспределения, пример).
17. Алгоритм распределительного метода. Пример применения метода для случая, когда поставка, переводимая по циклу, равна нулю.
18. Целочисленное программирование. Постановка задачи, графический метод решения, пример.
19. Метод Гомори (алгоритм метода, пример).
20. Задача о назначениях. Постановка задачи. Примеры применения задачи о назначениях к решению экономических проблем.
21. Венгерский метод. Алгоритм метода. Пример применения метода для решения задачи о назначениях.
22. Нелинейные задачи оптимизации. Постановка задачи, геометрический метод решения (алгоритм метода, пример).
23. Метод множителей Лагранжа (теорема о необходимых условиях локального минимума, комментарии к теореме). Теорема Вейерштрасса и следствие из неё. Пример применения метода множителей Лагранжа для решения нелинейной задачи оптимизации.
24. Метод штрафных функций. Примеры применения метода штрафных функций для решения задач оптимизации с ограничениями в форме равенств.
25. Метод штрафных функций. Примеры применения метода штрафных функций для решения задач оптимизации с ограничениями в форме неравенств.
26. Задачи выпуклого программирования (понятия выпуклого множества и выпуклой функции, особенности решения задач выпуклого программирования).
|
|
|
27. Градиентный метод с постоянным шагом. Пример применения данного метода для решения задачи оптимизации.
28. Метод скорейшего спуска. Пример применения данного метода для решения задачи оптимизации.
29. Метод Ньютона. Пример применения данного метода для решения задачи оптимизации.
30. Метод проекции градиента. Пример применения данного метода для решения задачи оптимизации.
31. Постановка задач многокритериальной оптимизации. Примеры многокритериальных задач в экономике.
32. Метод последовательных уступок. Алгоритм метода. Пример применения метода к решению задачи многокритериальной оптимизации выпуска продукции предприятием.
33. Метод равных и наименьших отклонений. Замещающая задача. Пример использования данного метода к решению конкретной экономической задачи.
34. Метод идеальной точки. Пример использования данного метода к решению конкретной экономической задачи.
35. Постановка задач оптимального управления. Принцип максимума для дискретных линейных задач оптимального управления.
36. Методы нелинейного программирования в задачах оптимального управления.
37. Динамическое программирование. Принцип оптимальности Р. Беллмана. Рекуррентные соотношения Беллмана. Численные методы расчета оптимальных программ.
38. Схемы динамического программирования в задачах оптимального управления.
39. Понятие марковского случайного процесса. Потоки событий. Уравнения Колмогорова. Процессы «рождения-гибели».
40. Экономико-математическая постановка задач массового обслуживания.
41. Модели систем массового обслуживания в коммерческой деятельности. СМО с отказами.
42. Модели систем массового обслуживания в коммерческой деятельности. СМО с ожиданием (очередью).
Образцы решения задач
Задача №1. Решить графическим методом типовую задачу оптимизации
Финансовый консультант фирмы «АВС» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25000$) в два наименования акций крупных предприятий в составе холдинга «МИЗУР».
Анализируются акции «МИЗУР-1» и «МИЗУР-2». Цены на акции: «МИЗУР-» - 5$ за акцию; «МИЗУР-2» - 3$ за акцию.
Клиент уточнил, что он хочет приобрести максимум 6000 акций обоих наименований, при этом акций одного из наименований должно быть не более 5000 штук.
|
|
|
По оценкам «АВС» прибыль от инвестиций в эти две акции в следующем году составит: «МИЗУР-1» - 1,1$; «МИЗУР-2» - 0,9$.
Задача консультанта состоит в том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?
Решение
Пусть х1 – количество акций «МИЗУР-1», а х2 – количество акций «МИЗУР-2».
Согласно условию:
5*x1 + 3*x2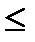 
25000 – клиент хочет вложить не более 25000$.
x1 +x2 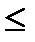6000–максимальное количество акций обоих типов 6000 шт.
x1 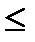5000, x2 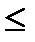5000 –максимальное количество акций одного типа 5000 шт.
1,1* x1+0,9* x2 –прибыль от владения акциями
Таким образом, экономико-математическая модель имеет вид.
F(x) =1,1* x1+0,9* x2 → mах
При следующих ограничениях:
5x1 + 3x2 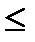25000 - I
x1 +x2 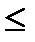6000- II
x1 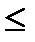5000 – III
x2 ≥ 5000 IV
x1 ≥ 0 V
x2 ≥ 0 VI
Этап 1. Определим множество решений первого неравенства. Оно состоит из решений уравнения и строгого неравенства. Решением уравнения служат точки прямой 5x1 +3 x2 = 25000.
Данной прямой принадлежат точки: при х1 = 0; х2 = 8333.33 т.е. точка с координатами (0;8333.33) и при х2 = 0; х1 = 5000 т.е. точка с координатами (5000; 0)
Построим прямую по двум точкам (0;8333.33) и (5000; 0). На графике обозначим эту прямую цифрой I.
Множество решений строгого неравенства есть одна из полуплоскостей, на которую делит плоскость построенная прямая. В качестве контрольной точки возьмем начало координат 0 < 25000. Неравенство выполняется. Значит областью допустимых решений (ОДР) неравенства является нижняя полуплоскость.
Аналогичным образом определим ОДР других неравенств.
Прямой x1 +x2 = 6000 принадлежат точки х1 = 0 х2 = 6000 (0; 6000) и х2 = 0 х1 = 6000 (6000; 0)
Построим прямую по двум точкам (0;6000) и (6000; 0). На рисунке обозначим эту прямую цифрой II. Множество решений неравенства нижняя полуплоскость, т.к. 0 < 6000 (неравенство выполняется). Значит областью допустимых решений (ОДР) неравенства является нижняя.
|
|
|
Прямая x1 =5000 параллельна оси ОУ. На рисунке обозначим эту прямую цифрой III. Множество решений неравенства левая полуплоскость.
Прямая x2 =5000 параллельна оси ОХ. На рисунке обозначим эту прямую цифрой IV. Множество решений неравенства нижняя полуплоскость.
x1 ≥ 0 V и x2 ≥ 0 VI Означает, что решение системы неравенств находится в первой координатной четверти.
Заштрихуем общую область для всех неравенств, обозначим вершины буквами АВСДО. Так как ОДР ограниченна, то функция имеет максимум и минимум.
Найдем координаты этих точек:
Точка А с координатами (0;5000) т.е. А(0;5000)
Точка В находится на пересечении прямых II и IV следовательно для нахождения ее координат запишем систему уравнений:
x1 + x2 = 6000
x2 = 5000
Решая эту систему уравнений находим координаты точки В
х2=5000
x1=1000
В(1000;5000)
Точка C находится на пересечении прямых I и II следовательно для нахождения ее координат запишем систему уравнений:
5x1 + 3x2 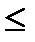25000 - I
x1 +x2 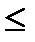6000- II
Решая эту систему уравнений находим координаты точки C
3х1+3х2=18000
5х1+3х2=25000
3х1+3х2-5х1-3х2=18000-25000=-7000
-2х1=-7000
х1=3500
х2=6000-3500=2500
C(3500;2500)
Координаты точки Д находятся на пересечении прямой II с осью координат входящей в ОДЗ, а именно (5000;0)
Д (5000;0)
Находим значения целевой функции в этих точках
F(A) = 1,1*0+0,9*5000=4500
F(B) = 1,1*1000+0,9*5000=5600
F(C) =1,1*3500+0,9*2500=6100
F(Д) = 1,1*5000+0,9*0=5500
Этап 2.
Приравниваем целевую функцию постоянной величине «а»:
1,1x1 +0,9x2 = а
это уравнение – множество точек, в которых F(x) принимает значения равное «а», получим семейство параллельных прямых каждая из которых называется линией уровня.
Пусть а = 0.
Вычислим координаты двух точек G (3600;-4400), О (0;0), построим прямую ОG.
Этап 3.
Для определения направления движения к оптимальному плану построим вектор – градиент, координаты которого являются частными производными целевой функции, т.е. С (С1;С2); С(1,1;0,9).
Построим вектор, соединив точки (1,1; 0,9) с началом координат.
При максимизации целевой функции необходимо передвигать линию уровня в направлении вектора градиента, а при минимизации в противоположном. Последняя точка ОДЗ, которую пересечет линия уровня и будет точкой максимума (или соответственно минимума).
Рис. 1. Графическое решение типовой задачи оптимизации
Таким образом, мах F=F(С)=6100. Максимальная прибыль будет получена при покупке 3500 шт. акций «МИЗУР-1», и 2500 шт. акций «МИЗУР-2».
При минимизации функции получаем, что минимальная прибыль составляет 0, при отказе от покупки акций.
|
|
|
