 |
График, как средство анализа ряда результатов наблюдений
|
|
|
|
ОСНОВЫ
НАУЧНЫХ ИССЛЕДОВАНИЙ
Учебное пособие для студентов заочного факультета
Часть 2
Санкт-Петербург
УДК 001.89
Коллектив авторов: Воробьев А.А., Иванов И.А., Меркушева В.С., Урушев С.В., Шадрина Н.Ю.
Основы научных исследований: Учебное пособие для студентов заочного факультета/ Под ред. Проф. И.А. Иванова. Часть 2 – СПб.: ПГУПС, 2012. –52 с.
В учебном пособии представлены: рабочая программа дисциплины, задание на контрольную работу, списки рекомендуемой литературы, краткий конспект лекций.
Рассматриваются вопросы организации научно-исследовательской работы в России, методология и основные методы научного исследования, а также законы и формы мышления. Приведены основные этапы научного исследования, включая выбор темы и заканчивая результатами научного исследования, структура отчета и этап внедрения законченных разработок. Описаны наиболее распространенные методы оценки полученных результатов. Даны элементы теории вероятностей и характеристики распределения случайных величин, некоторые методы оценки результатов измерений и определение эмпирических закономерностей. Приведены рекомендации по обработке результатов эксперимента. Категория «качество» рассмотрена как объект научного исследования. Отмечены особенности различных школ управления качеством и методы оценки качества продукции. Показаны направления, характеризующие качество жизни.
ОСНОВЫ
НАУЧНЫХ ИССЛЕДОВАНИЙ
Краткий конспект лекций для студентов заочного факультета
(продолжение)
Содержание
4. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ И ОЦЕНКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ.. 5
|
|
|
4.1. Результат измерения и его характеристики.. 5
4.2. Элементы теории вероятностей и характеристики распределения случайных величин.. 6
4.3. Методы оценки результатов измерений.. 14
4.4. Определение эмпирических закономерностей.. 18
5. КАЧЕСТВО КАК ОБЪЕКТ НАУЧНОГО ИССЛЕДОВАНИЯ.. 28
5.1. Эволюция развития науки управления качеством.. 28
5.2. Становление и развитие научных школ в области управления качеством.. 31
5.2.1. Американская школа. 31
5.2.2. Японская школа. 34
5.2.3. Российская школа. 35
5.3. Оценка качества. 38
5.3.1. Показатели качества. 38
5.3.2. Методы оценки качества продукции. 41
5.4. Качество жизни как объект научного исследования. 45
Вопросы и задания для самопроверки к главе 5. 48
Библиографический список. 50
4. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ И ОЦЕНКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
4.1. Результат измерения и его характеристики
При проведении экспериментальных исследований измерения являются почти непременной составной частью любого процесса исследования, от очень сложного до очень простого [10]. Но для измерений характерно то, что никогда они не являются заключительной частью какого-либо процесса деятельности. Измерения сами по себе являются процессом, завершающим этапом которого является «результат измерения». А за результатом измерения обязательно следует действие, даже тогда, когда измерения являются составной частью действия (или работы) автоматической установки. Иногда это действие кажется бездействием.
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств.
Под точностью результата измерений понимают одну из его характеристик (правильность, прецизионность), отражающую близость к нулю погрешности.
Погрешность результата измерения – это отклонение результата измерения от истинного значения измеряемой величины. Так как истинное значение может быть получено только в результате бесконечного процесса измерений и требует непрерывного совершенствования методов и средств измерений, то оно всегда остается неизвестным. В практических целях вместо истинного значения используется действительное значение измеряемой величины, т.е. значение, полученное экспериментальным путем и настолько близкое к истинному, что в рамках поставленной измерительной задачи может быть использовано вместо него. Таким образом, погрешность измерения может быть выражена зависимостью:
|
|
|
, (4.1)
где 
- измеренное значение величины; 
– действительное значение величины.
Значение ΔХ получило название абсолютной погрешности измерения. Абсолютная погрешность измерения выражена в единицах измеряемой величины. К сожалению, судить по значению абсолютной погрешности о качестве измерения нельзя. Действительно, если известно, что погрешность измерения составляет ±1 мм, то оценить его качество затруднительно. Необходимо сопоставить значение абсолютной погрешности и значение измеренной величины. Эта задача решается введением понятия относительной погрешности измерения. Относительная погрешность измерения рассчитывается как отношение абсолютной погрешности к действительному (или измеренному) значению величины. Относительную погрешность выражают в долях единицы или в процентах в соответствии с зависимостью:
или 
(4.2)
По закономерности появления погрешности делятся на систематические и случайные. При этом, как правило, самостоятельного значения они не имеют, а рассматриваются в качестве составляющих собственно погрешности измерения.
Систематической погрешностью измерения называется составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины [11].
Случайной погрешностью измерения называется составляющая погрешности, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью.
4.2. Элементы теории вероятностей и характеристики распределения случайных величин
Наличие случайной составляющей погрешности измерения приводит к тому, что для получения результата измерения целесообразно рассматривать измеряемые величины как случайные. Кроме того, сами случайные погрешности могут быть определены только с привлечением аппарата теории вероятностей, которая представляет собой науку, изучающую закономерности случайных явлений. Теория вероятностей устанавливает закономерности только для массовых явлений, т.е. таких явлений, которые могут повторяться многократно при одних и тех же условиях.
|
|
|
Случайным называется событие, которое в данном опыте может произойти или не произойти. Обозначим случайное событие А и будем иметь в виду, что большинство событий при измерениях понимаются как выполнение соотношения
,
где 
- допустимое значение 
.
Каждое из событий в опыте обладает какой-то степенью возможности: одни – большей, другие – меньшей. Для количественного сравнения случайных событий по степени их возможности используется количественная характеристика каждого случайного события, которая выражается числом тем большим, чем более возможно данное событие. Эту характеристику называют вероятностью случайного события и обозначают, как правило, Р. Таким образом, вероятность случайного события является численной мерой объективной возможности этого события и определяется по формуле:
, (4.3)
где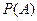 
– вероятность появления случайного события А в опыте (эксперименте, испытаниях и т.д.);
– число случаев появления события А;
– общее число каких-либо событий, появляющихся (могущих появиться) в результате проведения опыта, включая событие 
.
Определение числа – числа всех возможных исходов опыта – часто весьма затруднительно, но самое главное, что в эксперименте попросту невозможно ввиду ограниченной возможности повторения опытов. Число – количество раз, когда событие 
в результате опыта наступило, в эксперименте также определяется на основе ограниченного числа опытов. Поэтому на практике вместо вероятности используют частоту появления случайного события :
|
|
|
, (4.4)
где 
– частота появления события в проведенных опытах;
– количество раз, когда событие наступило;
– общее число результатов опытов.
Частоту ввиду ее использования в роли вероятности на практике называют статистической вероятностью.
Свойства случайной величины исчерпывающе описываются законом распределения случайной величины, который представляет собой соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Случайные величины можно разделить на дискретные и непрерывные. Значения дискретной случайной величины могут быть перечислены. Значения непрерывной случайной величины непрерывно заполняют некоторый интервал. Случайные погрешности измерений относятся к непрерывным случайным величинам, но проявляются часто в виде некоторого набора значений, т.е. дискретно. Поэтому к ним применимы понятия и непрерывных и дискретных случайных величин.
Для дискретной случайной величины удобной формой описания закона распределения является ряд распределения – таблица, в которой перечислены возможные значения случайной величины 
и соответствующие им значения вероятности 
(табл. 4.1).
Таблица 4.1.
Ряд распределения
|
| 
| 
| 
| … | 
| 
|
|
| 
| 
| 
| … | 
| 
|
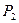
Еще одной, более удобной, универсальной и часто применяемой на практике формой описания закона распределения случайной величины является функция распределения 
, которая определяет вероятность того, что случайная величина 
будет принимать значения, меньшие некоторого ограничения
(4.5)
Функция распределения – это неубывающая функция, при 
при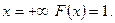 
График функции распределения непрерывной случайной величины представлен на рис. 4.1, а дискретной – на рис. 4.2.
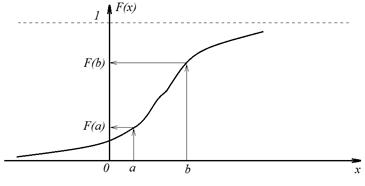
Рис. 4.1. График функции распределения непрерывной случайной величины
Функция распределения дискретной случайной имеет вид:
Рис. 4.2. График функции распределения дискретной случайной величины
Так как функция распределения непрерывной случайной величины (см. рис. 4.1) является непрерывно дифференцируемой, то для ее описания часто пользуются первой производной* 
, или плотностью распределения. Плотность распределения представляет собой одну из форм описания закона распределения, применяемых для непрерывных случайных величин. Плотность распределения обозначается, как правило, 
или 
. График плотности распределения представлен на рис. 4.3.
Рис. 4.3. График плотности распределения непрерывной случайной величины
Взаимосвязь между функцией распределения и плотностью распределения случайной непрерывной величины имеет вид:
|
|
|
(4.6)
Поскольку функция распределения – функция неубывающая (см. рис. 4.1), то плотность распределения есть функция неотрицательная, т.е. кривая распределения лежит выше оси абсцисс (см. рис. 4.3). Граничные значения функции распределения: 
.
Поэтому справедливо равенство:
(4.7)
Из зависимости (4.7) следует, что площадь, ограниченная кривой плотности распределения и осью абсцисс в интервале значения 
, равна единице. Вероятность того, что значение случайной величины принадлежит интервалу значений 
, равна разности значений функции распределения на границах этого интервала (см. рис. 4.1):
(4.8)
или площади под кривой плотности распределения, опирающейся на этот интервал (см. рис. 4.3).
Величина площади рассчитывается по зависимости:
(4.9)
Законы распределения позволяют решать любые практические задачи, связанные со случайными величинами, и в этом их безусловное достоинство. Наибольшее удобство для практического использования предоставляют числовые характеристики случайной величины – математическое ожидание и дисперсия случайной величины, которые характеризуют значение случайной величины и ее разброс соответственно.
Математическое ожидание случайной величины 
характеризует положение некоторого среднего значения случайной величины возле которого группируются возможные её значения.
Значение случайной величины x может быть определено величиной среднего арифметического значения, полученного по результатам многократных наблюдений этой величины.
(4.10)
Легко представить случай, когда для двух рядов измерений средние арифметические значения равны. Значит, одного этого значения недостаточно, чтобы охарактеризовать случайную величину. Необходима характеристика разброса. В качестве ее можно принять разность значений 
, полученных при измерениях результатов. Эта характеристика получила название размаха значений случайной величины.
Однако при равенстве и средних арифметических значений, и размахов два ряда измерений будут отличаться степенью группирования (концентрации) полученных результатов, например, относительно среднего арифметического значения. Подходящей характеристикой, позволяющей индивидуализировать разброс результатов многократных измерений, является суммирование величины их отклонений от среднего арифметического значения. Эта характеристика получила название дисперсии случайной величины 
. По определению дисперсия случайной величины – это математическое ожидание квадрата соответствующего отклонения случайной величины от ее математического ожидания 
:
Дисперсия случайной величины имеет размерность квадрата размерности собственной величины, что затрудняет использование дисперсии в практике метрологических работ. Поэтому в метрологии чаще используется понятие «среднее квадратическое отклонение» S (х), которое принимается равным положительному корню квадратному из значения дисперсии (При приближенных вычислениях среднее квадратическое отклонение обозначают через 
вместо 
(сигма)):
(4.11)
Вычисление 
на практике производится при ряде допущений. Во-первых, принимается, что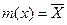 
. Правильнее было бы 
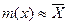, и это приближение тем грубее, чем меньше значений получено при измерениях. Во-вторых, принимается, что 
. Правильнее было бы 
. Подобные допущения приводят к тому, что расчетные значения численных характеристик смещены относительно своих действительных значений. Поэтому в практике метрологических работ, как правило, для определения среднего квадратического отклонения применяется формула вида:
, при 
(4.12)
Корректировка знаменателя в зависимости (4.12) позволяет компенсировать приведенные выше допущения за счет увеличения значения . При большом числе измерений (
) корректировка знаменателя не сказывается на величине 
; при малом – имеет большое значение, причем тем больше, чем меньше .
Форма кривой плотности распределения (см. рис 4.3) отражает вид функции 
. Во многих характерных случаях эти функции исследованы и результатами этих исследований пользуются на практике. Среди наиболее часто употребляемых распределений прежде всего необходимо выделить так называемое нормальное распределение, или распределение Гаусса. Это обусловлено тем, что если случайная величина представляет собой сумму трех и более составляющих, то ее распределение, независимо от формы распределения слагаемых, описывается уравнением:
(4.13)
Максимум функции достигается в точке 
(математическое ожидание случайной величины) и равен 
. С возрастанием нормальная кривая становится более пологой, т.е. прижимается к оси и растягивается вдоль неё. При уменьшении нормальная кривая стягивается к прямой 
. Точка называется центром распределения вероятностей, или центром распределения.
График функции нормального распределения представлен на рис. 4.4.
Рис. 4.4. График функции распределения нормального закона
В связи с тем, что большинство процессов измерений характеризуются большим числом составляющих погрешности измерения и это предоставляет право без проведения каких бы то ни было исследований принять для случайной погрешности нормальное распределение, нормальный закон стандартизован и является одной из двух установленных в нормативной документации форм законов распределения, применяемых при обработке результатов многократных измерений.
4.3. Методы оценки результатов измерений
Погрешности результата измерения физической величины дают представление о том, какие цифры в его числовом значении являются сомнительными. Поэтому нет смысла выражать погрешность результата измерения большим числом цифр. Достаточно ограничиться одной значащей цифрой или двумя, если вторая является пятеркой. Две значащие цифры удерживаются в числовых значениях погрешности только при ответственных и точных измерениях.
Округлять числовое значение результата измерения следует [10] в соответствии с числовым разрядом значащей цифры погрешности, т.е. числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.
График, как средство анализа ряда результатов наблюдений
Результаты ряда наблюдений одной и той же величины представляют собой набор отличающихся друг от друга чисел. Разница между результатами наблюдений, остающаяся после исключения систематических погрешностей, объясняется наличием случайных погрешностей. В первоначальном виде такой ряд можно оценить только очень приближенно, т.е. установить, велик ли разброс погрешностей. Уловить же какой-либо закономерности этого ряда на глаз по числам очень трудно. Дальнейшая математическая обработка с использованием приемов, описанных далее, позволяет характеризовать случайные погрешности.
Однако при математической обработке исчезает один признак ряда результатов измерений – их последовательность. Теория случайных погрешностей построена на предположении, что каждое единичное измерение самостоятельно и не зависит от других, а следовательно, не зависит от их последовательности [10].
В действительности, отказываясь от фактора последовательности, уравнивая правомерность каждого единичного измерения, мы лишается возможности оценивать некоторые характерные особенности всего ряда, в частности, степени наблюдения, указания об одинаковой тщательности наблюдений, неизменности условий измерений и т.п. Выявлению этих особенностей может помочь графическое изображение ряда результатов наблюдений в их реальной последовательности.
Графики целесообразно строить до начала математической обработки результатов измерений. Они дают основание для решения вопроса о пригодности полученного ряда для математической обработки.
В процессе измерения появляются грубые погрешности – это погрешности, не характерные для процесса или технологии, приводящие к явным искажениям результатов измерения. При оценке грубых промахов приходится прибегать к обычным методам проверки статистических гипотез.
Проверяемая гипотеза состоит из утверждений, что результат измерений не содержит грубой погрешности, а является одним из значений случайной величины. Обычно проверяют наибольшее 
и наименьшее 
значения результатов измерений. Для проверки гипотез используются следующие критерии [12, 13]:
Если число измерений 
, то может быть использован критерий Шовине. В этом случае грубой ошибкой (промахом) считается результат 
, если разность 
превышает значения 
, определяемые в зависимости от числа измерений:
,
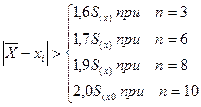где – СКО, полученное по формуле (4.12).
2. Критерий Романовского, используемый при числе измерений 
. При этом вычисляют отношение
и полученное значение 
сравнивают с теоретическим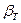 
при выбираемом уровне значимости 
(см. табл. 4.2). Уровень значимости – это вероятность отвергнуть верную гипотезу при статистической проверке гипотезы. Обычно при обработке результатов измерений её значение принимают в пределах 0,05…0,1.
Таблица 4.2
| Уровень значимости q | Число измерений n | ||||||
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,64 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
Если β≥β т, то результат хi считается промахом и отбрасывается.
3. Критерий трёх сигм (3σ) – наиболее распространенный (σ≈S). Он используется, когда количество измерений n≥ 20…50. В этом случае считается, что результат, полученный с вероятностью Р = 0,003, маловероятен и его можно квалифицировать как промах. Т.е. сомнительный результат xi должен быть исключен из измерений, если
.
Методы проверки нормального закона распределения случайных величин. При статистической обработке результатов измерений особую роль играет проверка соответствия распределения случайных величин нормальному закону, которому чаще всего подчиняются результаты большинства случайных измерений, что необходимо для обоснованного выбора доверительных границ результатов измерений и оценки точности измерений [14]. В наибольшей степени этой цели соответствует критерий 
(критерий Пирсона) – хи квадрат.
Для этой цели необходимо количество измерений 40 и более.
Обычно принимается следующий порядок решения задачи [14].
Диапазон полученных результатов измерений делят на r интервалов шириной Δ xi (i = 1, 2, …, r).
Для каждого интервала подсчитывают частоты mi , равные количеству результатов, лежащие в каждом i- м интервале.
Определяют частоту появления величины 
в каждом интервале:
,
где n – количество измерений, индекс «*» означает статистическую оценку.
Находят оценку средней плотности распределения 
случайной величины xi в каждом интервале Δ xi:
.
Строят гистограмму распределения величины xi, откладывая по оси абсцисс результаты наблюдений в виде интервалов Δ xi в порядке возрастания индекса i, а по оси ординат – оценку средней плотности распределения 
, получая прямоугольник с высотой 
.
Естественно, что площадь всех построенных прямоугольников равна единице, поскольку в нее входят все 100% наблюдений:
.
При построении гистограммы число интервалов r выбирают в зависимости от числа измерений n, исходя из соотношений: при n = 40…100 r = 7…9, а при n = 100…500, r = 8…12, а масштабы по осям гистограммы рекомендуется принимать такими, чтобы отношение ее высоты к основанию составляло 5: 8 (рис. 4.5).
Соединяя середины отрезков, получают полигон распределения. Характер ломаной линии позволяет сделать предположение о виде распределения, что дает возможность с большей долей вероятности подобрать соответствующую кривую распределения.
Рис. 4.5 Полигон и гистограмма распределения
Если СКО и математическое ожидание полигона распределения близки к значению СКО и математическому ожиданию кривой нормального распределения, то этот вид распределения можно положить в основу гипотезы о правомерности такого предположения.
Поскольку предположение основано на результатах опытных данных случайных величин, оно должно быть подтверждено обычными методами математической статистики по критериям согласия. При числе наблюдений более 40 рекомендуется принимать критерий согласия χ 2 - Пирсона.
4.4. Определение эмпирических закономерностей
Разнообразные способы получения информации о закономерностях, присущих тому или иному объекту исследования, можно разделить на две группы.
Наблюдения, когда исследователь не вмешивается в ход наблюдаемого процесса, ограничиваясь упорядоченной регистрацией значений интересующих его величин.
Эксперимент, когда ход процесса и регистрируемые значения величины зависят от последовательности изменений некоторых других величин, задаваемой исследователем (т.е. исследователь активно вмешивается в ход процесса).
Каждая группа способов имеет свои достоинства и недостатки. Введение искусственных изменений переменных, влияющих на состояние объектов исследования, позволяет целенаправленно и быстро получить искомые зависимости между переменными. Однако для того чтобы исследуемый эффект достаточно отчетливо проявился на фоне различных шумов, могут требоваться значительные изменения переменных. Для многих промышленных объектов это оказывается невозможным, поскольку такой эксперимент может привести к недопустимому по технологическим условиям режиму и даже к аварийным ситуациям. Кроме того, чтобы исключить при проведении опытов непредусмотренные режимы, значения неизменяемых переменных должны быть стабилизированы. Только при выполнении данного условия отдельные опыты обладают достаточной воспроизводимостью, а результаты достоверны. Требуемую стабильность неизменяемых переменных сравнительно легко можно обеспечить на лабораторных и полупромышленных установках. В производственных же условиях добиться стабильности весьма сложно, а во многих случаях невозможно. Например, для производств, где перерабатывается природное сырье, изменение переменных процесса не зависит от желания экспериментатора. Именно в этом случае применяется метод наблюдений, при использовании которого экспериментатор вынужден ожидать проявления интересующих его закономерностей, что значительно удлиняет время экспериментирования. Надо также иметь в виду, что описания, полученные на основании результатов наблюдений, справедливы лишь для имевшего место диапазона изменений переменных и, следовательно, носят частный характер.
Таким образом, метод проведения активного эксперимента предпочтителен. Однако в условиях плохой воспроизводимости опыта практически единственно возможным является метод наблюдений.
Успех применения экспериментальных методов тем более ощутим, чем выше уровень теоретических знаний об исследуемом объекте. В то же время следует отметить, что эмпирические методы в ряде случаев позволяют получить некоторое теоретическое представление о механизме исследуемого процесса и практически оценить теоретические предпосылки, имеющие часто односторонний, субъективный характер.
Не останавливаясь подробно на экспериментальных методах исследования, следует отметить некоторые из них [15,7]. На практике часто возникает задача определения влияния на состояние объекта исследования (конструкция, технологический процесс) факторов, имеющих только качественную оценку или не поддающиеся измерению, например, при выяснении влияния различных свойств сырья на качество изделий. Решение подобных задач составляет предмет дисперсионного анализа.
Если объект исследования по технологическим, техническим или экономическим соображениям не допускает преднамеренного варьирования входных переменных в необходимом диапазоне, то для накопления статистического материала применяется пассивный эксперимент, заключающийся в наблюдении и регистрации значений входных и выходных переменных в режиме нормального функционирования исследуемого объекта.
Выбор структуры модели является наиболее неформализуемой процедурой эксперимента, так как исследователь до начала эксперимента, как правило, не располагает необходимой априорной информацией.
Построение модели существенно упрощается, если в качестве ее составляющих используются полиномы, которые следует включать в уравнение регрессии. Модели полиномиального вида имеют преимущество в связи с тем, что с их помощью аналитическая функция (4.14) может быть описана достаточно точно.
(4.14)
Но прежде чем приступить к проведению эксперимента, необходимо выделить наиболее существенные входные величины (факторы) из всей совокупности входных величин, оценить степень корреляции между ними и исключить из числа подлежащих регистрации те из них, которые сильно коррелированны с другими. Выделение наиболее существенных входных переменных производят, например, методом априорного ранжирования [7, 16].
Как известно, любую функцию, если она не имеет бесконечных разрывов, можно разложить в степенной ряд Тейлора. Поэтому в теории эксперимента чаще всего математическое описание представляется в виде полинома путем разложения в ряд Тейлора:
, (4.15)
где b0, bj, bij, bjj – постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения эксперимента; п – число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента [16, 17].
Параметр bо функции (4.15) называется свободным членом уравнения; bj – линейными эффектами; bij – эффектами парного взаимодействия; bjj – квадратичными эффектами и т.п. Чем больше параметров модели (4.15), тем больше опытов придется провести.
Сначала целесообразно рассматривать простейшую и линейную модель
(4.16)
Если объект исследования (конструкция, технологический процесс) допускает целенаправленное изменение всех наиболее существенных входных переменных (факторов) по заранее определенным образом составленной программе в требуемых диапазонах варьирования, то применяется однофакторный или многофакторный активный эксперимент для построения математической модели объекта [16, 17].
Факторами называют наиболее существенные входные величины, принимающие в некоторый момент времени определенное значение. Область определения фактора, т.е. совокупность всех значений, которые принимает данный фактор, может быть непрерывной и дискретной. В задачах планирования активного эксперимента всегда используются дискретные области определения, а для факторов с непрерывной областью определения (температура, сила, время и т.п.) выбираются дискретные множества уровней. Кроме того фактор должен быть управляемым (поддерживаемым постоянным в течение опыта или меняющимся по заданной программе), однозначным (не являющимся функцией других факторов), измеряемым с до
|
|
|
