 |
Допускаемое и оптимальное значение решения задач линейного программирования. область допустимых решений.
|
|
|
|
K- объем производственных фондов
L-затраты труда
коэффициенты модели.
На основании производственной функции можно рассчитать следующие характеристики:
Потребность в одном из ресурсов при заданном объеме производства и величине др. ресурса.
2.Фондовооруженность труда:
* 
* 
Предельная норма замещения ресурса.
ПРЕДЕЛЬНАЯ НОРМА — количество одного ресурса (фактора производства), которое требуется для замены единицы другого ресурса без изменения объема выпуска (т. е. при движении вдоль изокванты).,1.) П. н.. определяется угловым коэффициентом изокванты, вдоль которой происходит замещение одного фактора производства другим.
Напр., для функции Кобба — Дугласа предельная норма замещения затрат труда производственными фондами имеет следующий вид:
.
Вопрос.Назначение динамической производственной функции.
Динамическая функция Кобба- Дугласа имеет следующий вид:
(t)
Динамическая производственная функция- отличается от статистической множителем A(t),чаще всего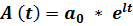 
.
Дифференцированную функцию по t получим соотношением между темпами прироста конечного продукта y и производственных факторов:
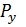=лямда + 
+β 
Таким образом, темп прироста конечного продукта есть сумма темпа и взвешивания суммы темпов прироста прочих факторов.
Если 
то это означает увеличение эффективности обоих производственных факторов.
Применение оптимальных моделей в экономике.
ОПТИМАЛЬНАЯ (ИЛИ ОПТИМИЗАЦИОННАЯ) МОДЕЛЬ [optimization model] — экономико-математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них.
|
|
|
В отличие от дескриптивной (описательной, балансовой) модели О. м. содержит наряду с уравнениями, описывающими взаимосвязи между переменными, также критерий для выбора — функционал (или, что то же, целевую функцию).
О. м. — основной инструмент экономико-математических методов. Обычно они очень сложны, насчитывают сотни и тысячи уравнений и переменных. Но общая структура таких моделей проста. Она состоит из целевой функции, способной принимать значения (на множестве значений переменных) в пределах области, ограниченной условиями задачи (области допустимых решений), и ограничений, характеризующих эти условия. Целевая функция в самом общем виде в свою очередь состоит из трех элементов: управляемых переменных, параметров (или также переменных), которые не поддаются управлению (напр., зависящих от внешней среды), и формы зависимости между ними (формы функции).
Математическая формулировка задач линейного программирования
Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Математическая формулировка задачи линейного программирования
Нужно максимизировать
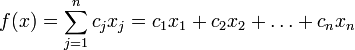
при условиях
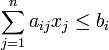
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют "основной" или "стандартной" в линейном программировании.
Допускаемое и оптимальное значение решения задач линейного программирования. область допустимых решений.
|
|
|
Решением (планом, вектором управления) задачи ЛП называется всякий вектор х из пространства En (En- n-мерное векторное пространство), в геометрической интерпретации – это точка векторного n-мерного пространства. Допустимым решением (планом) задачи ЛП называется такое решение задачи, которое удовлетворяет ее ограничениям g i (x1,x2,…, xn) bi, для всех i = 1,…, m.
Совокупность допустимых решений задачи называют областью допустимых решений (ОДР) задачи ЛП, которую, как правило, обозначают как D. Оптимальным решением х* называется такое допустимое решение, при котором целевая функция достигает своего оптимального, т. е. решение, удовлетворяющее условию max f(x) = f(x*). Величина f* = f(x*) называется оптимальным значением целевой функции.
область, в пределах которой осуществляется выбор решений. В принципе она может быть определена разными способами, вплоть до прямого перечисления входящих в нее элементов. В экономических задачах эта область, как правило, ограничена условиями задачи, наличными ресурсами. Эти ограничения могут быть более жесткими и менее жесткими, соответственно область свободы — более или менее широкой. Она не существует, если определяющие ее ограничения составляют несовместную систему уравнений.
В линейном программировании область допустимых решений (допустимый многогранник) всегда выпукла и всегда находится в неотрицательном подпространстве многомерного (n-мерного) пространства решений.
|
|
|
