 |
Доверительный интервал для математического ожидания при неизвестной дисперсии.
|
|
|
|
Пусть количественный признак Х генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратичное отклонение 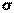 по исправленному среднему квадратичному отклонению
по исправленному среднему квадратичному отклонению  . Для этого найдем доверительный интервал, покрывающий неизвестный параметр
. Для этого найдем доверительный интервал, покрывающий неизвестный параметр 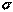 с надежностью
с надежностью 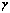 . В сущности, задача повторяет предыдущий раздел, но сейчас мы немного изменим обозначения для упрощения записи результата. Выражение для доверительной вероятности имеет вид
. В сущности, задача повторяет предыдущий раздел, но сейчас мы немного изменим обозначения для упрощения записи результата. Выражение для доверительной вероятности имеет вид 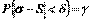 , где
, где 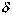 – абсолютная погрешность оценивания. Неравенство
– абсолютная погрешность оценивания. Неравенство 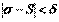 или равносильное ему неравенство
или равносильное ему неравенство 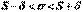 преобразуем к виду
преобразуем к виду 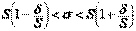 . Обозначим
. Обозначим 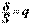 и, поскольку абсолютную погрешность оценивания мы выбираем достаточно малой, можно считать, что
и, поскольку абсолютную погрешность оценивания мы выбираем достаточно малой, можно считать, что 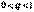 . Перепишем неравенство в виде
. Перепишем неравенство в виде  , домножим на
, домножим на 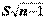 , получим
, получим 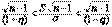 . Из предыдущего раздела известно, что случайная величина
. Из предыдущего раздела известно, что случайная величина 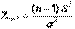 имеет распределение Пирсона
имеет распределение Пирсона 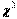 с
с 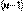 степенями свободы. Поэтому переменную
степенями свободы. Поэтому переменную 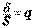 можно выразить через значения критических точек
можно выразить через значения критических точек 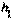 и
и 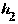 распределения Пирсона и записать эти значения в таблицу (в приложении значения параметра
распределения Пирсона и записать эти значения в таблицу (в приложении значения параметра  приведены в табл. 3). Вычислив по выборке значение
приведены в табл. 3). Вычислив по выборке значение  и найдя по таблице
и найдя по таблице 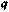 , получим искомый доверительный интервал для среднего квадратичного отклонения, покрывающий параметр
, получим искомый доверительный интервал для среднего квадратичного отклонения, покрывающий параметр 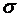 с заданной надежностью
с заданной надежностью 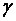 :
:  .
.
Замечание. В случаях, когда оценивается математическое ожидание при неизвестной дисперсии или дисперсия при неизвестном математическом ожидании, получающиеся при этом доверительные интервалы оказываются длиннее тех, что получены, когда, соответственно, дисперсия или математическое ожидание были известны. Это обстоятельство объясняется тем, что наличие дополнительной информации позволяет сузить пределы, в которые можно заключить оцениваемый параметр при заданной надежности.
|
|
|
Задача 4. В условиях задачи 3 найти доверительный интервал для среднего квадратичного отклонения 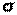 с надежностью
с надежностью 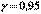 .
.
Решение задачи 4. Для удобства вычислений и наглядности еще раз представим таблицу значений.
Частичные интервалы 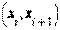
| (5;10) | (10;15) | (15;20) | (20;25) | (25;30) |
| Частоты | |||||

| 7,5 | 12,5 | 17,5 | 22,5 | 27,5 |
Объем выборки: 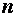 = 20, среднее выборочное значение
= 20, среднее выборочное значение 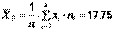 , выборочная дисперсия
, выборочная дисперсия 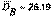 , исправленная дисперсия
, исправленная дисперсия 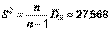 , исправленное выборочное среднее квадратичное отклонение
, исправленное выборочное среднее квадратичное отклонение 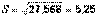 . Доверительный интервал для среднего квадратичного отклонения определяется неравенством
. Доверительный интервал для среднего квадратичного отклонения определяется неравенством 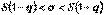 . По заданной надежности
. По заданной надежности 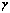 = 0,95 и объему выборки
= 0,95 и объему выборки 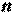 = 20 найдем, с помощью табл. 3, параметр
= 20 найдем, с помощью табл. 3, параметр  :
: 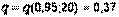 . Доверительный интервал для среднего квадратичного отклонения
. Доверительный интервал для среднего квадратичного отклонения 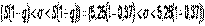 или
или 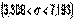 . Таким образом, интервал
. Таким образом, интервал 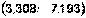 покрывает параметр
покрывает параметр 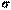 с надежностью
с надежностью 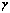 = 0,95.
= 0,95.
72 сопряженные регрессионные прямые До сих пор обсуждалась регрессия у на х: 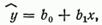 т. е. у рассматривалась как зависимая переменная, 1 — как объясняющая. На практике часто встречаются экономические явления, между которыми существует взаимодействие, т. е. переменная у зависит от переменной х и, наоборот, переменная х зависит от у. В таких случаях говорят о логически обратимых регрессиях. При переходе от одной постановки задачи к другой нельзя просто из уравнения (2.9) выразить х через у. Это связано с тем, что эмпирические точки лежат не на прямой, а подвержены рассеянию (см. диаграмму рассеяния в разделе 2.1). Фиксированному значению х может соответствовать несколько значений у, а данному значению у — несколько значений переменной х. Чем больше разброс точек на диаграмме рассеяния, тем больше будут отличаться друг от друга регрессионные прямые, соответствующие различному направлению зависимости. Уравнения регрессии не выводимы друг из друга. Так как объектом изучения являются стохастические связи между переменными, при исследовании зависимостей между двумя переменными теоретически всегда существуют две различные регрессионные прямые, которые называются сопряженными. Все рассуждения относительно регрессии у на приведенные в разделах 2.3 и 2.4, верны для регрессии на у. В предположении линейной зависимости в качестве функции регрессии примем уравнение прямой
т. е. у рассматривалась как зависимая переменная, 1 — как объясняющая. На практике часто встречаются экономические явления, между которыми существует взаимодействие, т. е. переменная у зависит от переменной х и, наоборот, переменная х зависит от у. В таких случаях говорят о логически обратимых регрессиях. При переходе от одной постановки задачи к другой нельзя просто из уравнения (2.9) выразить х через у. Это связано с тем, что эмпирические точки лежат не на прямой, а подвержены рассеянию (см. диаграмму рассеяния в разделе 2.1). Фиксированному значению х может соответствовать несколько значений у, а данному значению у — несколько значений переменной х. Чем больше разброс точек на диаграмме рассеяния, тем больше будут отличаться друг от друга регрессионные прямые, соответствующие различному направлению зависимости. Уравнения регрессии не выводимы друг из друга. Так как объектом изучения являются стохастические связи между переменными, при исследовании зависимостей между двумя переменными теоретически всегда существуют две различные регрессионные прямые, которые называются сопряженными. Все рассуждения относительно регрессии у на приведенные в разделах 2.3 и 2.4, верны для регрессии на у. В предположении линейной зависимости в качестве функции регрессии примем уравнение прямой
|
|
|

По сравнению с регрессией у на х переменные в (2.28) поменяли свои места. Зависимой переменной, или переменной, подлежащей объяснению, в данном случае является х, а независимой, или объясняющей, переменной — у. Коэффициенты — параметры регрессии.
Параметр снова представляет собой аддитивную постоянную, соответствующую точке пересечения прямой регрессии (2.28) с осью абсцисс. Параметр называется коэффициентом регрессии х на у. Этот параметр показывает, на сколько единиц в среднем изменится значение переменной х, если значение переменной у изменится на одну единицу. Расчетные значения регрессии х интерпретируются так же, как у в случае регрессии у на х.
Из-за разброса эмпирических точек вокруг прямой регрессии снова можно рассматривать отклонения наблюдаемых значений переменной х от расчетных значений регрессии х, которые мы обозначим через 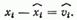 Значения являются реализациями случайной возмущающей переменной V. Эти значения — результат влияний на х не учтенных в функции регрессии (2.28) переменных-факторов, включая случайные флуктуации. Возмущающая переменная в статистическом смысле интерпретируется как ошибка спецификации регрессии (2.28). Переменную х можно тогда выразить как
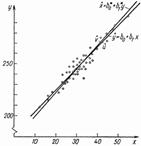
Значения являются реализациями случайной возмущающей переменной V. Эти значения — результат влияний на х не учтенных в функции регрессии (2.28) переменных-факторов, включая случайные флуктуации. Возмущающая переменная в статистическом смысле интерпретируется как ошибка спецификации регрессии (2.28). Переменную х можно тогда выразить как  Из сказанного выше следует, что интерпретация регрессионной прямой, параметров регрессии, расчетных значений функции регрессии х на у аналогична смысловому истолкованию тех же понятий при рассмотрении регрессии у на х. Должно быть принято во внимание только обратное направление зависимости, а также то, что отклонения опытных точек от линии регрессии измеряют по горизонтальной оси (рис. 15). Прямая регрессии х на у строится из условия минимизации суммы квадратов отклонений, измеренных по горизонтали:
Из сказанного выше следует, что интерпретация регрессионной прямой, параметров регрессии, расчетных значений функции регрессии х на у аналогична смысловому истолкованию тех же понятий при рассмотрении регрессии у на х. Должно быть принято во внимание только обратное направление зависимости, а также то, что отклонения опытных точек от линии регрессии измеряют по горизонтальной оси (рис. 15). Прямая регрессии х на у строится из условия минимизации суммы квадратов отклонений, измеренных по горизонтали: 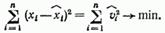 После нахождения частных производных по неизвестным парамет рам и приравнивая их нулю получаем так же, как в разделе 2.4, систему нормальных уравнений, решение которых дает нам искомые параметры:
После нахождения частных производных по неизвестным парамет рам и приравнивая их нулю получаем так же, как в разделе 2.4, систему нормальных уравнений, решение которых дает нам искомые параметры: 
|
|
|
Сравнивая формулы (2.32) и (2.33) с (2.22) и (2.23), видим, что они по своей сущности одинаковы. Только х заменено на у, а у — на х.
Такая же взаимообразная перестановка величин х и у происходит и в других формулах. В соответствии с этим (2.24) в случае регрессии х на у принимает вид
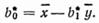
Пример
|
|
|


