 |
Расчёт трёхфазной цепи при соединении потребителей треугольником.
|
|
|
|
ЗАДАЧА 3
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ С ПРИЕМНИКАМИ,
СОЕДИНЕННЫМИ «ЗВЕЗДОЙ» И «ТРЕУГОЛЬНИКОМ»
К трёхфазной симметричной сети с линейным напряжением U л подключена цепь. Значения линейного напряжения U л, активного r, индуктивного xL и ёмкостного xC сопротивлений приёмников приведены в таблице.
Необходимо:
1. При соединении приёмников звездой с нейтральным проводом определить токи в линейных и нейтральном проводах, а также активную и реактивную мощности, потребляемые нагрузкой при симметричной системе напряжений на нагрузке. Построить топографическую диаграмму напряжений и на ней показать векторы всех токов.
2. Те же элементы трёхфазной нагрузки включить треугольником и определить фазные и линейные токи. Рассчитать значения активной и реактивной мощностей, потребляемых нагрузкой. Построить векторную диаграмму напряжений и токов для этого случая.
Схема 1
| U Л, В | Сопротивления, Ом | |||||
| r 1, Ом | r 2, Ом | L 2, мГн | r 3, Ом | L 3, мГн | С 3, мкФ | |
Таблица 1
Решение:
Расчет трехфазной цепи при соединении потребителей звездой.
Так как в схеме есть нейтральный провод, то напряжение на фазах нагрузки равно соответствующему фазному напряжению источника питания (обмотки генератора считаем соединенными звездой, а сопротивлением нейтрального провода пренебрегаем):
Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту:
ω = 2π f = 2 ∙ 3,14 ∙ 50 = 314 рад/с.
Определяем реактивные индуктивные сопротивления:
xL 2 = ω L 2 = 314 ∙ 40∙ 10–3 =12, 56 Ом,
xL 3 = ω L 3 = 314 ∙ 45∙ 10–3 = 14,13 Ом.
|
|
|
Определяем реактивное емкостное сопротивление:
xС 3 =1/(ω С 3) = 1/(314 ∙ 500 ∙ 10–6) = 6,369 Ом.
Используем выражение для однофазных цепей:
Применяем эту формулу и получаем полные сопротивления фаз в следующем виде:
Токи в линейных проводах (фазные токи нагрузки) определяем с помощью закона Ома:
Ток в нейтральном проводе находим по первому закону Кирхгофа:
Полные мощности фаз:
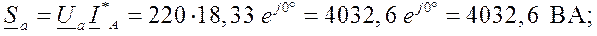
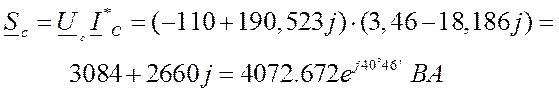
Так как вещественная часть полной мощности есть активная мощность цепи, а мнимая часть – реактивная, то, просуммировав отдельно вещественные, а затем мнимые части мощностей трех фаз, определяем трехфазную активную и реактивную мощности.
Активная трехфазная мощность:
Реактивная трехфазная мощность:
Полная мощность:
Активная трехфазная мощность нагрузки:
Относительная ошибка вычислений для активной мощности
Реактивная трехфазная мощность нагрузки также определяется суммой реактивных мощностей потребителей каждой из фаз.
Суммарная реактивная мощность всех потребителей:
Относительная ошибка вычислений для активной мощности:
Ошибка менее одного процента допускается. Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно.
Векторную диаграмму размещаем на комплексной плоскости с осями +1 и + j. Выбираем масштаб векторов тока равным 10 А/деление, а векторов напряжения – 40 В/деление.
Векторная диаграмма при соединении потребителей “ звездой ” с нейтральным проводом.
Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем схему соединения потребителей треугольником (рисунок 2)
Рисунок 2
Записываем в комплексной форме линейные напряжения на нагрузке:
Сопротивления фаз нагрузки в комплексной форме:
|
|
|
Фазные токи определяем по закону Ома:
Для определения линейных токов используем первый закон Кирхгофа для точек a, в, c схемы.
Полные комплексные мощности:
Трехфазная активная мощность:
Трехфазная реактивная мощность:
Трехфазная полная мощность:
Сделаем проверку расчетов:
Рассчитаем мощность нагрузки:
Относительная ошибка вычислений для активной мощности:
Рассчитаем суммарная реактивная мощность:
Относительная ошибка вычислений для реактивной мощности:
Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно.
Векторную диаграмму токов для нагрузки, соединенной треугольником, строим в масштабе на комплексной плоскости относительно осей +1 и + j.
Векторная диаграмма для нагрузки соединённой треугольником.
|
|
|
