 |
Схема выбора с возвращениями.
|
|
|
|
Определение. Если при выборке m элементов из n элементов сами элементы возвращаются обратно и упорядочиваются, то такое размещение называется размещением с повторениями.
Определяются и обозначаются следующим образом:

Размещения с повторениями могут отличаться друг от друга элементами, их порядком, количеством повторений элементов.
Определение. Если при выборке m элементов из n элементов элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями.
Определяются и обозначаются следующим образом:

Пусть в множестве с n элементами есть k различных элементов. При этом первый элемент повторяется  , второй
, второй  – раз и так далее, причем
– раз и так далее, причем 
Определение. Перестановки из n элементов данного множества называется перестановками с повторением.
 - вот эта хрень – полиномиальный коэффициент
- вот эта хрень – полиномиальный коэффициент
5. Биномиальная и полиномиальная схемы
Биномиальная схема – схема независимых испытаний (биномиальные вероятности)
Она же – схема Бернулли (когда многократно повторяется один и тот же опыт с одними и теме же вероятностями).
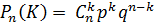

6. Статистическое определение вероятности
Классическое определение не требует проведения опыта. В то время как реальные прикладные задачи имеют бесконечное число исходов, и классическое определение в этом случае не может дать ответа. Поэтому в таких задачах будем использовать статическое определение вероятностей, которое подсчитывают после проведения эксперимента или опыта.
Статической вероятностью P(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний.
|
|
|

7. Аксиоматика теории вероятностей
Классическое определение вероятности случайного события предполагает конечное число всех исходов испытания. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно. В этом случае, если позволяют обстоятельства, используют понятие геометрической вероятности.
Геометрической вероятностью события A называется отношение меры области, благоприятствующей появлению события A, к мере всей области исходов Ω

(если представить двумерный график, то мера А – какая-нибудь фигура (типа там произойдет событие), а мера Ω - весь график вообще.
Пусть каждому событию A ставится в соответствие некоторое число P(A), которое удовлетворяет общепринятой системе аксиом Колмогорова:
1. Вероятность любого события заключена между нулем и единицей:
0 <= P(A) <= 1
P(Ω) = 1
2. Если A и B независимые события (A * B = Ø), то P(A+B) = P(A)+P(B).
3. Если имеется счетное множество несовместных событий A1, A2,..., An,...(Ai * Aj = Ø при i ≠ j), то 
8. Условная вероятность
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

9. Формула полной вероятности
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

10. Формула Байеса
формула Байеса позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных).
P(A/Hk), P(Hk) – априорные(доопытные) вероятности

- вероятность справедливости самой гипотезы (послеопытная, апостериорная) вероятность
11. Независимые испытания, схема Бернулли
Биномиальная схема – схема независимых испытаний (биномиальные вероятности)
Она же – схема Бернулли (когда многократно повторяется один и тот же опыт с одними и теме же вероятностями).
|
|
|


12. Случайные величины и их распределения
Случайная величина – измеримая функция, которая принимает свое значение с некоторыми вероятностями.
Чтобы узнать все о случайное величине, надо знать EX, DX и функцию распределения или функцию плотности
Дискретные случайные величины – задаются значениями и вероятностями.
1. биномиальная случайная величина – появляется в схеме независимых испытаний Бернулли – в каждом опыте либо успех либо неудача
| … | n |
C вероятностью: 
EX = np
DX = npq
0 < p < 1
q = 1 – p
2. Геометрическая случайная величина (стреляем по мишени)
| k | ∞ | |||
| p | qp | q2p | qk-1p | … |
EX = 
DX = 
3. Распределение Пуассона (редких событий)
| … | n |
с вероятностью: 
EX = λ
DX = λ
|
|
|


