 |
Т.е. количество информации, приобретаемое при полном выяснении состоянии некоторой физической системы, равно энтропии этой системы.
|
|
|
|
Учитывая (1.1), при а=2, получим
Ix= –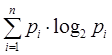 
, (1.5)
где pi = P(X ~ xi)
Формула (1.5) означает, что информация Ix есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком.
Действительно, для получения Ix каждое значение 
(логарифм вероятности i -го состояния) со знаком минус множится на вероятность этого состояния и все такие произведения складываются. Естественно каждое отдельное слагаемое - log pi рассматривать как частную информацию, получаемую от отдельного сообщения, состоящего в том, что система Х находится в состоянии xi. Обозначим эту информацию 
:
Тогда информация Ixпредставится как средняя (или полная) информация, получаемая от всех возможных отдельных сообщений с учетом их вероятностей.
Если все возможные состояния системы одинаково вероятны (p1=p2=…=pn=1/n), то формула (1.5) может быть преобразована к виду:
Ix=log2n 
, (1.6)
Если информация выражена в двоичных единицах, то ей можно дать довольно наглядное истолкование, а именно: измеряя информацию в двоичных единицах, мы условно характеризуем ее числом ответов «да» или «нет», с помощью которых можно приобрести ту же информацию.
Сообщение, уменьшающее неопределенность знаний человека в два раза несет для него один бит информации.
Рассмотрим систему с двумя состояниями:
| xi | x1 | x2 |
| pi | p1 | p2 |
Чтобы выяснить состояние этой системы, достаточно задать один вопрос: находится ли система в состоянии х1?
Ответ «да» или «нет» доставляет некоторую информацию, которая достигает своего максимального значения 1, когда оба состояния равновероятны: p1=p2=1/2, т.о. максимальная информация, даваемая ответом «да» или «нет», равна одной двоичной единице.
Если информация от какого-то сообщения равна n двоичным единицам, то она равносильна информации, даваемыми n ответами «да» или «нет» на вопросы, поставленные так, что «да» и «нет» одинаково вероятны.
|
|
|
Если поставить вопросы так не удается, можно утверждать только, что минимальное число вопросов, необходимых для выяснения содержания данного сообщения, не меньше, чем информация, заключенная в сообщении.
Пример. Некто задумал любое целое число Х от единицы до восьми
1 ≤ Х ≤ 8,
а нам предлагается угадать его, поставив минимальное число вопросов на каждый из которых дается ответ «да» или «нет».
Решение: Определяем информацию, заключенную в сообщении, какое число задумано. Априори все значения Х от 1 до 8 одинаково вероятны: 
, и формула (1.6) дает
Минимальное число вопросов, которые нужно поставить для выяснения задуманного числа, не меньше трех.
В данном случае можно, действительно, обойтись тремя вопросами, если сформулировать их так, чтобы вероятности ответов «да» или «нет» были равны.
Пусть, например, задумано число «пять», мы этого не знаем и задаем вопросы:
Вопрос 1. Число Х меньше пяти?
Ответ: Нет.
(Вывод: Х – одно из чисел 5,6,7,8.)
Вопрос 2. Число Х меньше семи?
Ответ: Да.
(Вывод: Х -одно из чисел 5,6.)
Вопрос 3. Число Х меньше шести?
Ответ: Да.
(Вывод: число Х равно пяти.)
Легко убедиться, что тремя такими (или аналогичными) вопросами можно установить любое задуманное число от 1 до 8)
Информация и алфавит
Алфавитный подход к измерению информации позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т. е. он не зависит от субъекта (человека), воспринимающего текст.
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
|
|
|
x = log2N, (т. к. N = 2х),
где N – мощность алфавита. Следовательно, в 2-символьном алфавите каждый символ «весит» 1 бит (log22 = 1); в 4-символьном алфавите каждый символ несет 2 бита информации (log24 = 2); в 8-символьном – 3 бита (log28 = 3) и т. д.
один символ из алфавита мощностью 256 (28) несет в тексте 8 бит информации. Такое количество информации называется байт. Алфавит из 256 символов используется для представления текстов в компьютере.
1 байт = 8 бит.
Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
V = K x,
где x – информационный вес одного символа в используемом алфавите.
Для измерения информации используются и более крупные единицы:
1 Кбайт (килобайт) = 210 байт = 1024 байта
1 Мбайт (мегабайт) = 220 байт = 1024 Кбайта
1 Гбайт (гигабайт) = 230 байт = 1024 Мбайта
1 Тбайт (терабайт) = 240 байт = 1024 Гбайта
пример 4 книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?
Решение. Мощность компьютерного алфавита равна 256. один символ несет 1 байт информации. Значит, страница содержит 40 х 60 = 2400 байт информации. Объем информации в книге (в разных единицах):
2400 х 150 = 3600 байт.
360000/1024 = 351,5625 Кбайт.
351,5625/1024 = 0,34332275 Мбайт.
Основы алгоритмизации
Алгоритм и его свойства
Прежде чем обратиться к рассмотрению конкретных алгоритмов, необходимо определиться с тем, что же такое алгоритм. Традиционно считается, что самый первый алгоритм был придуман древнегреческим математиком Евклидом. В современной математике понятие алгоритма является ключевым понятием, которое восходит к работам выдающегося узбекского математика IX века Аль-Хорезми.
Примеры алгоритмов в широком смысле этого слова можно встретить и в повседневной жизни. Так, поваренная книга является сборником алгоритмов, описывающих процессы приготовления пищи.
Компьютерные программы представляют собой алгоритмы, записанные средствами языков программирования.
Исчерпывающее определение алгоритма дано выдающимся соотечественником А. А Марковым. алгоритм – это точное общепринятое предписание, определяющее процесс преобразования исходных данных в искомый результат.
|
|
|
Исполнитель алгоритма –это тот объект или субъект, для управления которым составлен алгоритм.
Система команд исполнителя (СКИ) – это вся совокупность команд, которые исполнитель умеет выполнять.
Алгоритм должен обладать следующими свойствами: понятностью, точностью, конечностью.
Понятность: алгоритм составляется только из команд, входящих в СКИ исполнителя.
Точность: каждая команда алгоритма управления определяет однозначное действие исполнителя.
Конечность (или результативность): выполнениеалгоритма должно приводить к результату за конечное число шагов.
Среда исполнителя: обстановка, в которой функционирует исполнитель.
Определенная последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Полный набор данных: необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата).
для того чтобы сделать алгоритм более наглядным, часто используют блок-схемы.
Блок-схема алгоритма представляет собой систему блоков, соединенных между собой линиями, которые указывают последовательность выполнения блоков. Направление на линии связи между блоками указывается стрелкой в конце линии. Если линия связи направлена сверху вниз и слева направо, то стрелка на этой линии не ставится.
Блоки изображаются геометрическими фигурами, внутри которых дается текстоформульная информация. Блок, организующий ввод или вывод данных, изображается параллелограммом. Для изображения разветвления используется ромб, внутри которого условие разветвления. для обозначения начала и конца алгоритма используются прямоугольники с закругленными углами. Допускается нумерация блоков путем разрыва верхней стороны их контура и записи на месте разрыва номера блока.
При составлении блок-схемы алгоритма рекомендуется располагать ее на одной странице и придерживаться правил, установленных ГОСТ 19.002-80 «Схемы алгоритмов и программ. Правила выполнения», ГОСТ 19.003-80 «Схемы алгоритмов и программ. Обозначения условные графические» и ГОСТ 19.701-90 «Единая система программной документации. СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ, ДАННЫХ И СИСТЕМ. Обозначения условные и правила выполнения», дата введения которого 01.01.92. ГОСТ 19.701-90 имеет статус действующего в настоящее время, разработан на основе ГОСТ 19.002-80 и ГОСТ 19.003-80.
|
|
|
ОБЩИЕ ТРЕБОВАНИЯ:
– Схемы алгоритмов, программ данных и систем состоят из имеющих заданное значение символов, краткого пояснительного текста и соединяющих линий.
– Схемы могут использоваться на различных уровнях детализации, причем число уровней зависит от размеров и сложности задачи обработки данных. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом.
– Схема – графическое представление определения, анализа или метода решения задачи, в котором используются символы для отображения операций, данных, потока, оборудования т.д.
Правила выполнения схем
1.1 Для облегчения вычерчивания и нахождения на схеме зон устанавливают с учетом минимальных размеров символов, изображенных на данном листе. Допускается один символ размещать в двух и более зонах, если размер символа превышает размер зоны.
1.2 Координаты зоны представляют:
по горизонтали – арабскими цифрами слева направо в верхней части листа;
по вертикали – прописными буквами латинского алфавита сверху вниз в левой части листа.
1.3 Координаты зон в виде сочетания букв и цифр присваиванию символам, вписанным в поля этих зон, например А1, А2, А3, В1, В2, В3 и т.д.
При выполнении схем от руки, если поле листа не разбито на зоны, символам присваивают порядковые номера.
1.4 В пределах одной схемы, при выполнении ее от руки, допускается применять не более двух смежных размеров ряда чисел, кратных 5.
1.5 Линии потока должны быть параллельны линиям внешней рамки схемы.
1.6 Расстояние между параллельными линиями потока должны быть не менее 3 мм, между остальными символами схемы – не менее 5 мм.
1.7 Записи внутри символа или рядом с ним должны быть краткими. Сокращения слов и аббревиатуры, за исключением установленных государственными стандартами, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится.
1.8 Для удобства детализации программы должны быть использованы символы «Процесс», «Решение», «Модификация», «Ввод-вывод» и «Пуск-останов», при этом внутри символов на расстоянии не менее 0,25 а проводят тонкую линию (размер а по ГОСТ 19.003-80)
|
|
|
1.9 Записи внутри символов должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока. Вид а должен быть прочитан как вид б.
 | |||||
 | |||||
 | |||||
а б
Фрагменты ГОСТ 19.003-80
|
|
|
