 |
Аналитическая геометрия на плоскости
|
|
|
|
Элементы линейной алгебры, векторная алгебра,
Аналитическая геометрия. Комплексные числа
Элементы линейной алгебры
1. 1. Матрица. Основные понятия. Матрицей А размера  называется множество
называется множество  элементов расположенных в виде прямоугольной таблицы из
элементов расположенных в виде прямоугольной таблицы из  строк и
строк и  столбцов, имеющей вид:
столбцов, имеющей вид:
 .
.
Если  , то А называется квадратной матрицей. Квадратные матрицы размера
, то А называется квадратной матрицей. Квадратные матрицы размера  и
и  называются матрицами второго и третьего порядка, соответственно.
называются матрицами второго и третьего порядка, соответственно.
Квадратная матрица, элементы главной диагонали которой единицы, а все остальные элементы нули, называется единичной:
 ,
,  .
.
Матрица вида  называется матрицей–столбцом.
называется матрицей–столбцом.
Пусть даны две матрицы:
 ,
,  .
.
1) Суммой (разностью) матриц А и В называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц
А и В:
 .
.
2) Умножение матрицы на число. При умножении матрицы А на число  , на это число умножаются все элементы матрицы:
, на это число умножаются все элементы матрицы:
 .
.
3) Произведение матрицы А на матрицу В обозначается символом АВ и определяется равенством:
 .
.
т. е. элемент матрицы произведения, стоящий в  -й строке и
-й строке и  -м столбце, равен сумме произведений соответственных элементов
-м столбце, равен сумме произведений соответственных элементов  -й строки матрицы А и
-й строки матрицы А и  -го столбца матрицы
-го столбца матрицы  . Например.
. Например.
 .
.
Необходимо знать, что  (в общем случае), но в некоторых случаях равенство может иметь место. Например:
(в общем случае), но в некоторых случаях равенство может иметь место. Например:  .
.
1. 2. Определитель. Определителем второго порядка, соответствующим матрице  называется число, вычисляемое по формуле:
называется число, вычисляемое по формуле:
 .
.
Аналогично, определителем третьего порядка называется число, определяющееся равенством:
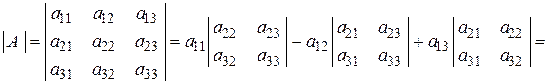
 .
.
Минором  элемента
элемента  определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащий данный элемент. Алгебраическим дополнением
определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащий данный элемент. Алгебраическим дополнением  элемента
элемента  называется произведение его минора на
называется произведение его минора на  , где
, где  и
и  номера строки и столбца, содержащих данный элемент. Например:
номера строки и столбца, содержащих данный элемент. Например:
|
|
|
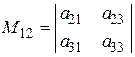 , тогда
, тогда 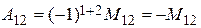 .
.
Пример 1. Даны матрицы
 ;
;  ;
; 
Найти матрицу  и вычислить ее определитель.
и вычислить ее определитель.
Решение.
 ,
,
 ,
,

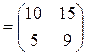 ,
,
т. е. 
 .
.
 .
.
1. 3. Нахождение обратной матрицы.
Матрица  называется обратной по отношению к матрице
называется обратной по отношению к матрице  , если произведения
, если произведения  и
и  равны единичной матрице:
равны единичной матрице:
 .
.
Пусть  , тогда
, тогда  найдется по формуле:
найдется по формуле:
 ,
,
где  — определитель матрицы
— определитель матрицы  , а
, а  – алгебраическое дополнение элемента матрицы
– алгебраическое дополнение элемента матрицы  .
.
Если  , обратная матрица не существует (не определяется).
, обратная матрица не существует (не определяется).
Пример 2. Дана матрица  . Найти ей обратную.
. Найти ей обратную.
Решение. Вычисляем определитель матрицы:
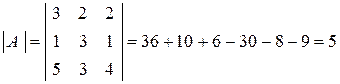 .
.
Находим алгебраические дополнения элементов этого определителя:
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
, 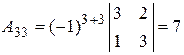 .
.
Следовательно,
 .
.
Проверка. Если обратная матрица найдена правильно, то должно выполняться равенство:  .
.

 .
.
1. 4. Решение систем линейных уравнений (СЛУ). Дана система трех линейных уравнений с тремя неизвестными:

Эту систему можно записать в матричном виде:  , где
, где
 ,
,  ,
,  .
.
1. 4. 1. Метод Крамера для решения СЛУ. Если  , то система имеет единственное решение и находится по формулам:
, то система имеет единственное решение и находится по формулам:
 ,
,  ,
,  ,
,
где  — определитель матрицы
— определитель матрицы  , а
, а
 ,
,  ,
, 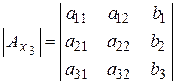 .
.
1. 4. 2. Метод Гаусса для решения СЛУ.

Допустим, что  (если
(если  , то изменим порядок уравнений, выбрав первым такое, в котором коэффициент при
, то изменим порядок уравнений, выбрав первым такое, в котором коэффициент при 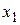 не равен нулю).
не равен нулю).
1 ШАГ. Делим уравнение (1) на  ; умножим полученное уравнение на
; умножим полученное уравнение на  и вычтем его из (2); затем умножим на
и вычтем его из (2); затем умножим на  и вычтем из (3). В результате приходим к системе:
и вычтем из (3). В результате приходим к системе:

2 ШАГ. Делим уравнение (5) на  , умножаем полученное уравнение на
, умножаем полученное уравнение на  и вычитаем его из (6). В результате система преобразуется к так называемому ступенчатому виду:
и вычитаем его из (6). В результате система преобразуется к так называемому ступенчатому виду:
|
|
|
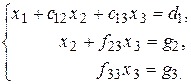
Из преобразованной системы все неизвестные определяются последовательно, начиная с  .
.
4. 3. Матричный метод решения СЛУ. Пусть дана система  . Домножим обе части данного выражения на
. Домножим обе части данного выражения на  слева, т. е.
слева, т. е.  , так как
, так как  , а
, а  , то придем к уравнению вида
, то придем к уравнению вида  . Это и будет решением СЛУ.
. Это и будет решением СЛУ.
Пример 3. Решить систему уравнений тремя способами:

Решение.
1) Метод Крамера. Запишем матрицу  и столбец свободных членов
и столбец свободных членов  :
:
 ,
, 
Решение данной системы найдем по формулам:
 ,
,  ,
,  ,
,
где  ,
,
 ,
,
 ,
,


Следовательно,
 ,
,  ,
,  ,
,
2) Метод Гаусса.

Умножим уравнения (а) на 3 и вычтем полученное уравнение из (б); затем умножим уравнение (а) на 4 и вычтем из уравнения (в), в итоге получим:

Разделим уравнение (д) на (-4); умножим полученное уравнение на (-5) и вычтем его из уравнения (е), получим:

Из последнего уравнения находим 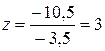 ; далее, из второго
; далее, из второго
уравнения:  ; из первого:
; из первого:  .
.
Итого  ,
,  ,
,  .
.
3) Матричный метод.

 ,
, 
 .
.
Решение данной системы найдем по формуле  .
.
Найдем  . Определитель матрицы
. Определитель матрицы  мы уже знаем
мы уже знаем  . Вычислим алгебраические дополнения для элементов определителя матрицы А.
. Вычислим алгебраические дополнения для элементов определителя матрицы А.
 ,
,  ,
, 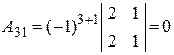 ,
,
 ,
,  ,
,  ,
,
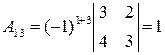 ,
,  ,
,  .
.
 .
.
 ,
,
значит решением данной системы будет  ,
,  ,
,  .
.
Аналитическая геометрия на плоскости
2. 1. Прямая линия
Общее уравнение прямой
 .
.
Две прямые  и
и  параллельны, если
параллельны, если 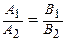 , перпендикулярны, если
, перпендикулярны, если  . Расстояние от точки
. Расстояние от точки  до прямой
до прямой  вычисляется по формуле:
вычисляется по формуле:
 .
.
Уравнение прямой с угловым коэффициентом:
 .
.
Угол  , отсчитанный против часовой стрелки от прямой
, отсчитанный против часовой стрелки от прямой 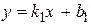 , до прямой
, до прямой  определяется формулой:
определяется формулой:
 .
.
Условие параллельности двух прямых:  ,
,
Условие перпендикулярности:  .
.
Уравнение прямой, проходящей через данную точку  , или уравнение пучка прямых:
, или уравнение пучка прямых:
 .
.
Уравнение прямой, проходящей через две данные точки  и
и 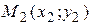 :
:
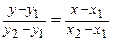 .
.
Угловой коэффициент прямой, проходящей через две точки:  .
.
Уравнение прямой в отрезках на осях:  .
.
Пример 1. Через точку  провести прямые параллельно, перпендикулярно и под углом
провести прямые параллельно, перпендикулярно и под углом  к прямой (АВ):
к прямой (АВ):  .
.

Решение. Уравнения прямых, проходящих через точку  :
:
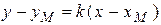 ,
,
 .
.
Найдем угловые коэффициенты искомых прямых. Прямая (АВ) задана общим уравнением:  . Выразив из него
. Выразив из него  , получаем уравнение с угловым коэффициентом
, получаем уравнение с угловым коэффициентом  ;
;  .
.
|
|
|
1.  .
.
Уравнение  :
:  или
или  .
.
2.  .
.
Уравнение  :
:  или
или  .
.
3. Прямая  образует с
образует с  угол
угол  . Обозначим ее угловой коэффициент через
. Обозначим ее угловой коэффициент через  и воспользуемся формулой
и воспользуемся формулой

 ;
;  =1. Имеем
=1. Имеем  , так как искомое
, так как искомое  может совпадать с
может совпадать с  или
или 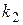 .
.
1)  ;
;  ;
;  .
.
2) 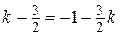 ;
;  ;
;  .
.
Искомые прямые
 :
:  или
или 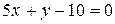 .
.
 :
:  или
или  .
.
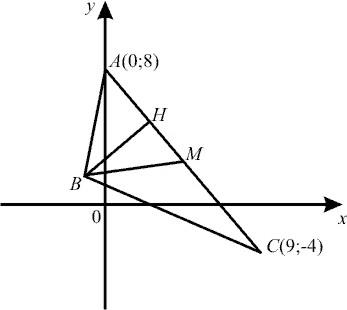 Пример 2.
Пример 2.  ;
;  ;
;  вершины треугольника. Найти уравнения стороны АС, высоты, медианы, проведенных из вершины В, длину этой высоты, угол А.
вершины треугольника. Найти уравнения стороны АС, высоты, медианы, проведенных из вершины В, длину этой высоты, угол А.
Решение. 1)Прямая (АС) проходит через две точки
 ;
;  ;
;
(АС): 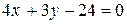 или
или 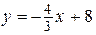 ;
; 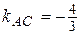 .
.
2) 
(ВН):  ;
; 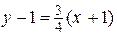 ;
;  .
.
3) ВМ – медиана, М – середина АС,
 ;
;  ;
;
(ВМ):  ;
;  ;
;  .
.
4) Длина высоты  равна расстоянию от точки В до прямой АС
равна расстоянию от точки В до прямой АС
 ;
;  (ед.).
(ед.).
5)  ;
; 
 ;
;
 ;
;  .
.
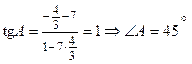 .
.
Кривые второго порядка
Уравнение  если А, В и С одновременно не равны нулю, задает на плоскости линию, которую называют кривой второго порядка.
если А, В и С одновременно не равны нулю, задает на плоскости линию, которую называют кривой второго порядка.
Если В =0 кривая имеет ось симметрии параллельную координатным осям. Будем рассматривать только этот случай.
Выделяя полный квадрат относительно каждой переменной x и y, уравнение  приводим к одному из следующих канонических видов:
приводим к одному из следующих канонических видов:
1.  – линии эллиптического типа:
– линии эллиптического типа:
 – эллипс с центром
– эллипс с центром  полуосями а и b.
полуосями а и b. 
Если  то уравнение запишется в виде
то уравнение запишется в виде

– окружность с центром  радиуса R.
радиуса R.
2.  – линии гиперболического типа:
– линии гиперболического типа:
 – гипербола с центром
– гипербола с центром  вещественной полуосью – а, мнимой полуосью – b.
вещественной полуосью – а, мнимой полуосью – b.

 – сопряженная гипербола с центром
– сопряженная гипербола с центром  вещественной полуосью – b, мнимой полуосью – а.
вещественной полуосью – b, мнимой полуосью – а.
3. 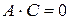 – линии параболического типа.
– линии параболического типа.
Здесь возможны четыре случая:
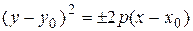 либо
либо  – параболы с вершиной
– параболы с вершиной  , где
, где  .
.
В первом случае – ось симметрии параллельна оси  , во втором –
, во втором – 
Если в уравнении знак “+”, ветви параболы направлены в положительном направлении оси симметрии, знак “–” — в противоположном.


Замечание. Возможны так называемые вырожденные случаи:
1)  :
:
 – точка
– точка  .
.
 – мнимый эллипс.
– мнимый эллипс.
2)  :
:  или
или

– пара пересекающихся прямых: 
3) 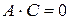 :
: 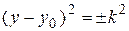 или
или  – пара мнимых прямых, пара параллельных прямых.
– пара мнимых прямых, пара параллельных прямых.
|
|
|
4. ВЕКТОРНАЯ АЛГЕБРА
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3.1. Координаты вектора.

Обозначим единичные векторы координатных осей соответственно 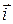 ,
,  ,
,  .
.  ,
, 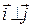 ,
,  ,
,  . Любой вектор
. Любой вектор  может быть единственным способом разложен на составляющие по координатным осям:
может быть единственным способом разложен на составляющие по координатным осям:

 ,
,  ,
,  ,
,
 .
.
Числа  ,
,  ,
,  проекции вектора на оси координат, называются координатами вектора
проекции вектора на оси координат, называются координатами вектора  в базисе
в базисе  .
.
3. 2. Основные действия с векторами.
Пусть  ,
,  ,
,  – скаляр.
– скаляр.
1°.  Û
Û 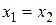 ,
,  ,
,  .
.
2°.  .
.
3°.  .
.
4°. Длина (модуль) вектора:  .
.
5°. Условие параллельности векторов:  ||
||  Û
Û  .
.
6°. Чтобы найти координаты вектора надо из координат его конца вычесть координаты начала  .
.
Пример. Найти длину вектора  , если
, если  ,
,  .
.
Решение. По 6°:  ,
,  . Его длина (4°):
. Его длина (4°):  (ед).
(ед).
3. 3. Скалярное произведение векторов есть число, вычисляемое по формуле:
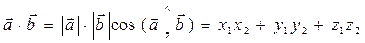 .
.
Угол между векторами:

Условие перпендикулярности векторов:  Û
Û  Û
Û  .
.
Проекция вектора  на направление
на направление  :
:  .
.
Пример. Найти угол между векторами  ;
;  .
.
Решение. Находим  ;
;  ,
,
 ;
;  ,
,
 .
.
3. 4. Векторное произведение.
Векторным произведением  на
на  называется вектор
называется вектор  , удовлетворяющим трем условиям
, удовлетворяющим трем условиям
1.  ,
,
2.  ;
;  ,
,
3.  образуют правую тройку, т. е. с конца вектора
образуют правую тройку, т. е. с конца вектора  вращение от
вращение от  к
к  , по наименьшему углу, выглядит против часовой стрелки.
, по наименьшему углу, выглядит против часовой стрелки.
Обозначают  .
.
Обратите внимание,  .
.
 — модуль векторного произведения численно равен площади параллелограмма, построенного на векторах
— модуль векторного произведения численно равен площади параллелограмма, построенного на векторах  и
и  как на сторонах.
как на сторонах.
Если известны координаты сомножителей, то
 .
.
Пример. Построить векторы  ,
,  ,
, 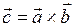 .
.
 ;
;  . Найти площадь параллелограмма, построенного на векторах
. Найти площадь параллелограмма, построенного на векторах  и
и  как на сторонах.
как на сторонах.
Решение. Найдем вектор  .
.
 .
.
Сделаем чертеж.

На векторах  и
и  , как на сторонах, строим параллелограмм ОАВD. Его площадь численно равна
, как на сторонах, строим параллелограмм ОАВD. Его площадь численно равна  , т. е. длине вектора
, т. е. длине вектора  .
.

 ;
;
Площадь параллелограмма  .
.
3. 5. Смешанное произведение трех векторов есть число
 .
.
В координатной форме:
 .
.
Модуль смешанного произведения  — численно равен объему параллелепипеда, построенного на векторах
— численно равен объему параллелепипеда, построенного на векторах  , как на сторонах.
, как на сторонах.
Смешанное произведение имеет знак плюс, если тройка векторов  — правая, минус, если тройка левая.
— правая, минус, если тройка левая.
Условие компланарности векторов. Векторы компланарны (лежат в одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю, т. е.
 .
.
3.6. Разложение вектора по базису.
Любые три вектора  ,
,  ,
,  , не лежащие в одной плоскости, могут быть приняты за базис в
, не лежащие в одной плоскости, могут быть приняты за базис в  . Всякий вектор
. Всякий вектор  может быть разложен по этому базису, т. е. представлен в виде
может быть разложен по этому базису, т. е. представлен в виде  .
.
Пример. Найти объем параллелепипеда, построенного на векторах
 ;
;  ,
,  .
.
Решение. Найдем смешанное произведение

 ,
,
Объем 
Пример. Убедиться, что векторы  не лежат в одной плоскости, написать разложение вектора
не лежат в одной плоскости, написать разложение вектора  по векторам
по векторам  если
если
|
|
|
 ;
; 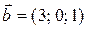 ;
;  ;
;  .
.
Решение. 1) Проверяем условие компланарности для векторов  .
.

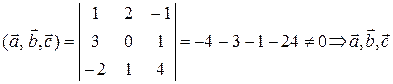 не лежат в одной плоскости и могут быть приняты за базис.
не лежат в одной плоскости и могут быть приняты за базис.
2) Разложим вектор  по векторам
по векторам  :
:
 .
.
Чтобы найти  запишем это равенство для каждой координаты
запишем это равенство для каждой координаты

Решив систему уравнений любым известным способом, находим  ;
;  ;
;  . Значит,
. Значит,  .
.
3. 7. Плоскость и прямая в пространстве
1. Общее уравнение плоскости. Уравнение плоскости есть уравнение первой степени относительно  :
:
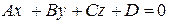 .
.
Вектор  перпендикулярен к плоскости.
перпендикулярен к плоскости.
2. Если плоскость проходит через точку 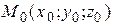 , то ее уравнение
, то ее уравнение
 .
.
3. Уравнение плоскости, проходящей через три точки  ,
,
 ,
,  :
:

4. Расстояние от точки 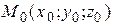 до плоскости
до плоскости 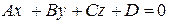 находится по формуле
находится по формуле

Пример. Найти расстояние до плоскости, проходящей через точки  ,
, 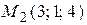 ,
,  , от начала координат.
, от начала координат.
Решение. Составим уравнение плоскости
 ,
,

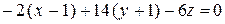 ;
;  .
.
Расстояние от начала координат  до плоскости
до плоскости
 .
.
5. Общие уравнения прямой записываются как линия пересечения двух плоскостей:

если  и
и 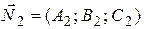 не коллинеарны.
не коллинеарны.
6. Канонические уравнения:

–прямая, проходящая через точку  в направлении
в направлении  .
.
7. Прямая, проходящая через две данные точки

8. Условия параллельности и перпендикулярности плоскостей, прямых, прямой с плоскостью определяются соотношениями направляющих векторов  и
и  . Например, если плоскости параллельны, то
. Например, если плоскости параллельны, то  , если прямая параллельна плоскости, то
, если прямая параллельна плоскости, то 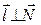 и т. п.
и т. п.
Пример. Через точку  провести прямую, перпендикулярно плоскости
провести прямую, перпендикулярно плоскости  .
.
Решение. Воспользуемся каноническими уравнениями прямой 
 , так как его длина несущественна, можно взять
, так как его длина несущественна, можно взять  . Имеем
. Имеем  :
:  .
.
Пример. Точки  ,
,  ,
,  ,
, 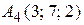 являются вершинами пирамиды. Вычислить 1) длину ребра
являются вершинами пирамиды. Вычислить 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 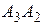 ; 3) площадь грани
; 3) площадь грани  ; 4) Объем пирамиды; 5) уравнения прямой
; 4) Объем пирамиды; 5) уравнения прямой  ; 6) уравнение плоскости
; 6) уравнение плоскости  ; 7) уравнение высоты, опущенной из вершины
; 7) уравнение высоты, опущенной из вершины  на грань
на грань  ; 8) длину этой высоты.
; 8) длину этой высоты.

Решение. Найдем координаты векторов — ребер:
 .
.
 ,
,  ,
,
 .
.
1) Длина вектора  .
.
2)  ,
,
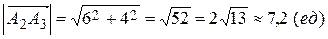 ,
,
Скалярное произведение:  ,
,
 ,
,
 .
.
Из таблиц (или с помощью калькулятора) находим  .
.
3) Площадь грани  .
.

Векторное произведение
 ;
;
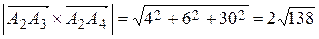 ,
, 
4) Объем пирамиды 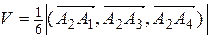 .
.
Смешанное произведение
 ,
,

 .
.
5) Уравнения прямой 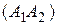 пишем как уравнение прямой, проходящей через две точки:
пишем как уравнение прямой, проходящей через две точки:
 ;
;  ;
;
 .
.
6) Уравнение плоскости  по трем точкам:
по трем точкам:
 .
.
 ;
;  ;
;
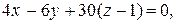
 .
. 
7) Уравнение высоты  . Канонические уравнения прямой:
. Канонические уравнения прямой:
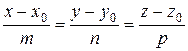 .
.
Прямая проходит через точку  , в качестве направляющего вектора возьмем вектор
, в качестве направляющего вектора возьмем вектор  — нормаль к плоскости
— нормаль к плоскости  .
.

8) Длина высоты может быть найдена как расстояние т.  от плоскости
от плоскости 

или
 ;
;  .
.
Комплексные числа
4.1. Комплексным числом называется выражение вида:
 ,
,
где  и
и  — любые действительные числа, а
— любые действительные числа, а  — так называемая мнимая единица, удовлетворяющая условию
— так называемая мнимая единица, удовлетворяющая условию
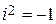 .
.
Числа  и
и  называются соответственно действительной и мнимой частями комплексного числа
называются соответственно действительной и мнимой частями комплексного числа  .
.
Комплексные числа можно представлять точками  плоскости
плоскости  или же векторами
или же векторами  этой плоскости.
этой плоскости.

4. 2. Длина  вектора
вектора  называется модулем комплексного числа и обозначается через
называется модулем комплексного числа и обозначается через  , так что
, так что  .
.
Угол


