 |
Функции нескольких переменных. Интегралы.
|
|
|
|
Материал выставлен на странице кафедры математики
http://www.swsu.ru/structura/up/fivt/kvm/student_mathematical_olympiads.php
В подготовительном этапе олимпиады могут принимать участие все студенты 1-2 курсов. Решения можно сдать Федоровой Н.Б. или своему преподавателю до 20 декабря. 15 декабря будут выложены указания к решениям. Решения предложенных задач будут доступны 21 декабря. Наиболее активные участники первого этапа будут приглашены в математический кружок по решению олимпиадных задач с целью подготовки к Всероссийским и Международным математическим олимпиадам. Участие в работе математического кружка дает возможность получить 3-6 дополнительных баллов в модульно-рейтинговой системе. Участие в олимпиадах также дает дополнительные баллы: в международных – 10; в республиканских – 8; вузовских – 6 баллов. За призовые места добавляется ещё 4 балла.
Алгебра
1.1. Найти 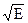 , где Е – единичная матрица второго порядка, т.е. решить матричное уравнение Х2 = Е.
, где Е – единичная матрица второго порядка, т.е. решить матричное уравнение Х2 = Е.
1.2. Построить график функции 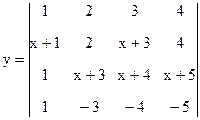 .
.
1.3. Вычислить:  .
.
1.4. Найти наименьшее  , при котором выполняется равенство:
, при котором выполняется равенство:
 .
.
1.5. Доказать, что матричное уравнение  , не имеет решений среди матриц с действительными элементами.
, не имеет решений среди матриц с действительными элементами.
1.6. Изобразите на плоскости aOb множество точек (a,b), для которых система 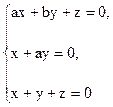 имеет более одного решения и найдите эти решения.
имеет более одного решения и найдите эти решения.
1.7. Докажите, что квадратная матрица второго порядка с положительными
элементами имеет собственный вектор с положительными координатами.
1.8. Доказать, что для любого действительного числа α
 . При каких α достигается знак равенства?
. При каких α достигается знак равенства?
2. Геометрия.Векторная алгебра и аналитическая геометрия
2.1. Определить вид треугольника АВС, если
|
|
|
а)  ,
,
б) 
в) 
2.2. Известно, что  и
и 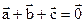 . Докажите, что
. Докажите, что
1) среди векторов нет ни одной пары коллинеарных;
2) вычислите значение выражения:  .
.
2.3. К вершине куба приложены три силы, равные по величине 1, 2, 3 и
направленные по диагоналям граней куба, выходящим из этой вершины.
Найти величину равнодействующей этих сил и углы, образуемые с
составляющими силами.
2.4. В пирамиде SABC AS = a, BC =b, угол между векторами 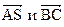 равен
равен
φ. Найти расстояние между серединами ребер АВ и CS.
2.5. Под действием некоторой силы точка двигалась по окружности
 . Действие силы прекратилось в тот момент, когда
. Действие силы прекратилось в тот момент, когда
точка занимала положение А(2;1). Определить дальнейшую траекторию
точки.
2.6. Парабола  пересекает окружность
пересекает окружность  в точках А и
в точках А и
В. Найти значение параметра 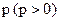 , если ΔОАВ (О – начало координат)
, если ΔОАВ (О – начало координат)
– правильный.
2.7. В треугольнике АВС точка Н – точка пересечения высот, О – центр опи-
санной окружности, М – середина ВС, F – основание высоты, проведенной
из вершины А. Прямоугольник HOMF имеет стороны НО = 11 и ОМ = 5.
Найти длину ВС.
Пределы.
3.1. Найдите пределы функций:
а)  ; б)
; б)  ; в)
; в) 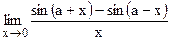 ;
;
г) 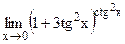 ; д)
; д)  .
.
3.2. Найдите n из уравнения 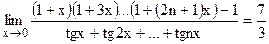 .
.
3.3. Докажите, что последовательность (xn), заданная формулами:
 , имеет предел и найдите его.
, имеет предел и найдите его.
Функция. Производная функции и её приложения.
4.1. Для многочлена n-ой степени Р(x) известно, что
 . Докажите, что корни уравнения
. Докажите, что корни уравнения
Р(x) = 0 не превосходят а.
4.2. Найдите  если
если  .
.
4.3. Фигура ограничена линиями:  ,
,  ,
,  . В какой точке
. В какой точке
 графика функции
графика функции  нужно провести к нему касательную
нужно провести к нему касательную
так, чтобы она отсекала от фигуры трапецию наибольшей площади?
4.4 Пусть f(x),  - заданная дифференцируемая функция. Докажите,
- заданная дифференцируемая функция. Докажите,
что уравнение  имеет хотя бы один корень.
имеет хотя бы один корень.
4.5. Найдите наименьшее значение функции 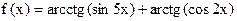 .
.
4.6. Найдите наименьшее значение ординаты середины отрезка длины а, кон-
цы которого расположены на параболе  .
.
|
|
|
Функции нескольких переменных. Интегралы.
5.1. Найдите кратчайшее расстояние между поверхностью 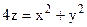
и плоскостью  .
.
5.2. При каких значениях параметра а производная функции z = x2 + y2 в
точке М(1,1) по направлению вектора  принимает
принимает
наибольшее значение?
5.3. Вычислите интеграл:  .
.
5.4. Найдите среднее значение функции  на отрезке [0,1].
на отрезке [0,1].
5.5. Вычислите 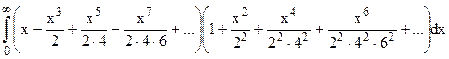 .
.
|
|
|


