Главная | Обратная связь | Поможем написать вашу работу!

Описание используемого математического аппарата при проведении расчетов

Регрессионный анализ

Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель <http://www.machinelearning.ru/wiki/index.php?title=%D0%A0%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C> есть функция независимой переменной и параметров с добавленной случайной переменной <http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D0%BB%D1%83%D1%87%D0%B0%D0%B9%D0%BD%D0%B0%D1%8F_%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F&action=edit>. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка <http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D0%BE%D1%88%D0%B8%D0%B1%D0%BA%D0%B0&action=edit>: сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента. Регрессионный анализ - раздел математической статистики <http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%81%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0> и машинного обучения <http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5>. Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины <http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D0%BB%D1%83%D1%87%D0%B0%D0%B9%D0%BD%D0%B0%D1%8F_%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D0%B0>. Относительно характера распределения этой величины делаются распределения, называемые гипотезой порождения данных. Для подтверждения или опровержения этой гипотезы выполняются статистические тесты <http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%82%D0%B5%D1%81%D1%82>, называемые анализом остатков <http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%BE%D0%B2&action=edit>. При этом предполагается, что независимая переменная не содержит ошибок. Регрессионный анализ используется для прогноза <http://www.machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7&action=edit>, анализа временных рядов <http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D1%85_%D1%80%D1%8F%D0%B4%D0%BE%D0%B2&action=edit>, тестирования гипотез <http://www.machinelearning.ru/wiki/index.php?title=%D0%A2%D0%B5%D1%81%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%B3%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%B7&action=edit> и выявления скрытых взаимосвязей в данных. Регрессия - зависимость математического ожидания <http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BE%D0%B6%D0%B8%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5&action=edit> (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть . Регрессионным анализом называется поиск такой функции 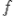, которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих. где 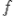- функция регрессионной зависимости, а - аддитивная случайная величина с нулевым мат ожиданием. Предположение о характере распределения этой величины называется гипотезой порождения данных <http://www.machinelearning.ru/wiki/index.php?title=%D0%93%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%B7%D0%B0_%D0%BF%D0%BE%D1%80%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD%D0%B8%D1%8F_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85&action=edit>. Обычно предполагается, что величина имеет гауссово распределение <http://www.machinelearning.ru/wiki/index.php?title=%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%BE%D0%B2%D0%BE_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5&action=edit> с нулевым средним и дисперсией .

Задача нахождения регрессионной модели нескольких свободных переменных ставится следующим образом. Задана выборка <http://www.machinelearning.ru/wiki/index.php?title=%D0%92%D1%8B%D0%B1%D0%BE%D1%80%D0%BA%D0%B0> - множество 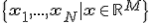значений свободных переменных и множество соответствующих им значений зависимой переменной. Эти множества обозначаются как , множество исходных данных .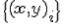

Задана регрессионная модель - параметрическое семейство функций 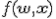зависящая от параметров и свободных переменных . Требуется найти наиболее вероятные параметры :

Функция вероятности зависит от гипотезы порождения данных и задается Байесовским выводом <http://www.machinelearning.ru/wiki/index.php?title=%D0%91%D0%B0%D0%B9%D0%B5%D1%81%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%B2%D1%8B%D0%B2%D0%BE%D0%B4&action=edit> или методом наибольшего правдоподобия <http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BD%D0%B0%D0%B8%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B5%D0%B3%D0%BE_%D0%BF%D1%80%D0%B0%D0%B2%D0%B4%D0%BE%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%B8%D1%8F>.

Метод наименьших квадратов

Метод наименьших квадратов - метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами - вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.

Задача метода наименьших квадратов состоит в выборе вектора , минимизируют ошибку . Эта ошибка есть расстояние от вектора до вектора . Вектор лежит в пространстве столбцов матрицы , так как есть линейная комбинация столбцов этой матрицы с коэффициентами . Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки 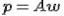, которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы .

Таким образом, вектор должен быть проекцией на пространство столбцов и вектор невязки должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов есть линейная комбинация столбцов с некоторыми коэффициентами , то есть это вектор . Для всех в пространстве , эти векторы должны быть перпендикулярны невязке :

Так как это равенство должно быть справедливо для произвольного вектора , то

Решение по методу наименьших квадратов несовместной системы , состоящей из уравнений с неизвестными, есть уравнение

которое называется нормальным уравнением. Если столбцы матрицы линейно независимы, то матрица обратима и единственное решение

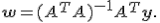
Проекция вектора на пространство столбцов матрицы имеет вид

Матрица 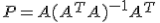называется матрицей проектирования вектора на пространство столбцов матрицы . Эта матрица имеет два основных свойства: она идемпотентна, , и симметрична, . Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.

Пусть имеем статистические данные о параметре y в зависимости от х. Эти данные представим в виде

х	х₁	х₂	…..	х _i	…..	х _n
y^*	y₁^*	y₂^*	......	y_i^*	…..	y_n^*

Метод наименьших квадратов позволяет при заданном типе зависимости y=φ(x) так выбрать ее числовые параметры, чтобы кривая y=φ(x) наилучшим образом отображала экспериментальные данные по заданному критерию. Рассмотрим обоснование с точки зрения теории вероятностей для математического определения параметров, входящих в φ(x).

Предположим, что истинная зависимость y от х в точности выражается формулой y=φ(x). Экспериментальные точки, представленные в табл.2, отклоняются от этой зависимости следствие ошибок измерения. Ошибки измерения подчиняются по теореме Ляпунова нормальному закону. Рассмотрим какое-нибудь значение аргумента х_i. Результат опыта есть случайная величина y_i,распределенная по нормальному закону с математическим ожиданием φ(x_i) и со средним квадратным отклонением σ_i, характеризующим ошибку измерения. Пусть точность измерения во всех точках х=(х₁, х₂, …, х_n) одинакова, т.е. σ₁=σ₂=…=σ_n=σ. Тогда нормальный закон распределения Y_i имеет вид:

В результате ряда измерений произошло следующее событие: случайные величины (y₁^*, y₂^*, …, y_n^*).

⇐ Предыдущая 123 Следующая ⇒

Воспользуйтесь поиском по сайту: