Порядок выполнения работы и обработка экспериментальных данных.

Лабораторная работа № 4

Определение модуля Юнга из растяжения.

Приборы и принадлежности:

1. Установка для исследования деформаций твёрдого тела.

2. Микрометр.

3. Рулетка.

4. Гири 2 и 4 кг.

Краткая теория

Деформацией твёрдого тела называют изменения его размеров и формы, обычно сопровождающееся и изменением объёма. В некоторых случаях, например, при деформации сдвига, изменение объёма тела может и не наблюдаться.

Деформации вызывают действием на него внешних сил или изменением температуры. Изучение физической природы процессов деформации является задачей молекулярной и атомной физики. Отметим лишь в общих чертах, что при деформации происходит смещение частиц, находящихся в узлах кристаллической решётки твёрдых тел из первоначальных положений равновесия в новые. Этому смещению препятствуют силы взаимодействия между частицами. В результате в деформированном теле возникают внутренние упругие силы.

Если после прекращения действия сил, вызвавших деформацию, она исчезает, то такую деформацию называют упругой. Неупругие деформации твёрдого тела сопровождаются необратимой перестройкой его кристаллической решётки. В этом случае наблюдаются остаточные, или пластическиедеформации. Упругие деформации имеют место тогда, когда внешние силы, вызывающие деформацию, не превосходят некоторого определённого для каждого конкретного тела предела, называемого пределом упругости. При установившейся упругой деформации результирующая внутренних сил, возникающая в теле, в любом сечении тела уравновешивает действующие на тело внешние силы. Поэтому, при установившейся упругой деформации величина внутренних сил может быть определена по величине внешних сил, приложенных к телу.

Величину внутренних упругих сил характеризуют напряжением, численно равным отношению результирующей упругих сил к единице площади сечения тела S, к которому эта сила приложена: (1). Когда сила F направлена по нормали к поверхности S, напряжение называют нормальным, если же сила направлена по касательной к этой поверхности, то напряжение называют тангенциальным (касательным). Мерой деформации является относительная деформация ε, равная отношению абсолютной деформации Δx к первоначальному значению величины х, характеризующей размеры или объём тела: (2).

Английский физик Р. Гук в 1574 – 1575 гг. опытным путём установил, что напряжения, возникающие в упруго деформированном теле, прямо пропорциональны величине относительной деформации: (3), где k – коэффициент пропорциональности, называемый модулем упругости. Соотношение (3) выражает закон Гука для любого вида упругих деформаций. Все возможные виды упругих деформаций твёрдого тела могут быть сведены к двум основным: деформации растяжения (или сжатия) и деформации сдвига. Упругая деформация продольного растяжения, например, проволоки, проявляется в изменении ее длины при изменении действующего на неё напряжения. Для этого к проволоке должна быть приложена растягивающая сила, действие которой равномерно распределено по всему сечению. Относительную деформацию ε в этом случае называют относительным удлинением, при этом закон Гука имеет вид: (4), где модуль упругости k = E получил название модуля Юнга. Модуль Юнга является постоянной величиной для данного вещества, и поэтому его значение зависит только от материала, из которого изготовлено деформируемое тело. Из формул (1) и (4) (сравнивая правые части уравнений) следует: 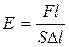(5).

Методика эксперимента

В данной работе деформируемым телом является тонкая проволока, к которой подвешивается груз весом Р. Следовательно, при установившейся упругой деформации величина внутренних упругих сил F уравновешивается внешней силой Р, действующей на проволоку. Таким образом, формулу (5) можно записать в виде: 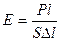(6), где P – вес груза, l – длина проволоки, S – площадь поперечного сечения проволоки (π R ², R – радиус проволоки), Δl – удлинение проволоки.

Рис. 1.

Входящие в формулу (6) величины P, l, и S определяются достаточно просто. Для нахождения удлинения проволоки Δl в данной работе применяется установка, изображённая на рисунке 1: 1 – линейка, снабжённая нониусом – 2 (элементы штангенциркуля), Р₀ – постоянная нагрузка, 3 – груз, подвешенный при измерениях, 4 – исследуемая проволока.

Порядок выполнения работы и обработка экспериментальных данных.

1. Рулеткой измерить длину проволоки l₀ с точностью до 5 мм.

2. Микрометром измерить диаметр проволоки (d=2R) с точностью до 0,01 мм.

3. Записать ближайшее деление шкалы (1) линейки N₀ к нулевому штриху нониуса (2) и номер по порядку штриха нониуса n_i, который совпадает с каким-либо делением основной шкалы линейки при натянутой проволоке l постоянной нагрузкой P₀ (а = N₀+ n_i·0,1 мм, а – это первоначальное показание штангенциркуля, где 0,1 мм – точность измерения штангенциркуля).

4. Подвесить груз (3) массой 2 кг (P₁=mg) и произвести отчёт по штангенциркулю как указано в пункте 3 (b = M₀+ m_i·0,1 мм, b – это показание штангенциркуля при нагрузке Р₁).

5. Удлинение проволоки первого измерения определяется как Δl= b - а.

6. Снять груз и повторить измерения, указанные в пунктах 3 и 4.

5. Повторить те же измерения с грузом массой 4 кг (P₂=mg).

№ п/п	l0 , мм	Δl0 , мм	d, мм	Δd, мм	а, мм	b, мм	Δl1, мм	Δ(Δl1), мм	e, %	Εср±ΔE, Па
1. 2. 3.
Ср. зн.

Результаты всех измерений и вычислений записать в таблицу, вычислить модуль Юнга (в системе СИ) и погрешности в его определении отдельно для опытов с гирей 2 кг и 4кг. Среднее значение модуля Юнга из всех опытов с его погрешностью записать в конце работы (E_ср±ΔE; e=ΔE/ E_ср).

Таблица 1 (m₁ = 2кг)

 

Аналогично составить таблицу 2 для m₂ = 4кг.

Контрольные вопросы

1. Что называется силой упругости и какова её природа?

2. Что называется деформацией тел? Какие виды деформаций вам известны?

3. В чём состоит закон Гука? Как он математически записывается в общей форме? Когда он справедлив?

4. Запишите закон Гука для деформации растяжения (сжатия). Каков физический смысл модуля Юнга и какова его размерность?

5. Изобразите примерный график зависимости упругого напряжения от значения относительной деформации (диаграмма растяжения). Что такое предел пропорциональности, предел упругости, предел прочности?

6. Какие материалы называют пластичными? Хрупкими? Приведите примеры, изобразите примерный вид диаграммы растяжения для пластичных и упругих тел.

Литература

1. Трофимова Т. И. Курс физики. - Учебное пособие для вузов. / 8-е изд., стер М.: Высшая школа, 2004. - 541

2. Савельев И. В. Курс физики: в 3 томах. Учебное пособие для втузов. СПб.: Лань, 2007. Т. 1. Механика. Молекулярная физика. - 350 с.

3. Матвеев А.Н. Механика и теория относительности [Текст]: учеб. пособие для вузов / А. Н. Матвеев. - 4-е изд., стер. - СПб: Лань, 2009. - 324 с

4. Александров Н. В., Яшкин А. Я. Курс общей физики. Механика. – М.: Просвещение, 1978.

 

Поделиться:

Воспользуйтесь поиском по сайту: