 |
Математические методы в экономике.
|
|
|
|
Линейное программирование.
Задача оптимального производства продукции.
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, и С. Потребность  на каждую единицу
на каждую единицу 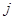 -го вида продукции
-го вида продукции  -го вида сырья, запас
-го вида сырья, запас 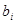 соответствующего вида сырья и прибыль
соответствующего вида сырья и прибыль 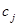 от реализации единицы
от реализации единицы 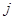 -го вида продукции заданы таблицей:
-го вида продукции заданы таблицей:
| Виды сырья | Виды продукции | Запасы сырья | |
| I | II | ||
| А | 
| 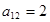
| 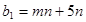
|
| В | 
| 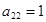
| 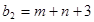
|
| С | 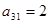
| 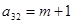
| 
|
| прибыль | 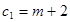
| 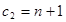
| |
| план (ед.) | 
| 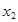
|
14.1.1Для производства двух видов продукции I и II с планом  и
и 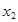 единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее
единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее 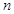 единиц обоих видов продукции.
единиц обоих видов продукции.
14.1.2В условиях задачи 14.1.1. составить оптимальный план 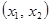 производства продукции, обеспечивающий максимальную прибыль
производства продукции, обеспечивающий максимальную прибыль 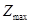 . Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
. Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
14.1.3Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль 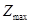 .
.
Транспортная задача.
На трех складах 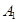 ,
,  и
и 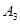 хранится
хранится 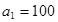 ,
, 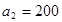 и
и  единиц одного и того же груза. Этот груз требуется доставить трем потребителям
единиц одного и того же груза. Этот груз требуется доставить трем потребителям 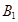 ,
, 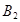 и
и 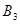 , заказы которых составляют
, заказы которых составляют 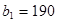 ,
, 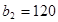 и
и 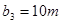 единиц груза соответственно. Стоимость перевозок
единиц груза соответственно. Стоимость перевозок  единицы груза с
единицы груза с  -го склада
-го склада 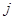 -му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
 потребности
запасы потребности
запасы
| 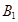
| 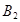
| 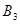
| |
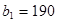
| 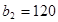
| 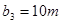
| ||
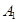
| 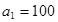
|  4 4
|  2 2
|  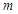
|

| 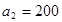
|  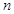
|  5 5
|  3 3
|
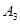
| 
|  1 1
|  
|  6 6
|
14.2.1Сравнивая суммарный запас 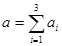 и суммарную потребность
и суммарную потребность 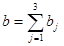 в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад 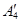 с запасом
с запасом 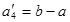 в случае
в случае 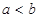 или фиктивного потребителя
или фиктивного потребителя 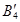 с потребностью
с потребностью 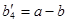 в случае
в случае 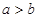 и положив соответствующие им тарифы перевозок нулевыми.
и положив соответствующие им тарифы перевозок нулевыми.
|
|
|
14.2.2Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.)
14.2.3Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
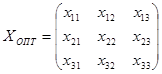 ,
,
обеспечивающий минимальную стоимость перевозок 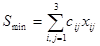 . Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
Матричные игры.
14.3.1 Игра 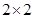 задана матрицей
задана матрицей
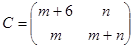
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.)
14.3.2 Игра задана матрицами
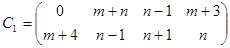 для
для 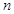 - четного
- четного
и
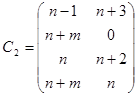 для
для 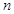 - нечетного.
- нечетного.
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
Математические методы в экономике.
15.1 Сетевое планирование.
Прогресс производства сложной продукции разбивается на отдельные этапы, зашифрованные номерами 1, 2,..., 10. 1 – начальный этап производства продукции, 10 – завершающий. Переход от  -го этапа к
-го этапа к 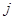 -му этапу назовем операцией. Возможны выполнения операций
-му этапу назовем операцией. Возможны выполнения операций 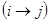 и их продолжительности
и их продолжительности  задаются таблицей.
задаются таблицей.
| N п/п | шифр операции | продолжительность операции | 15.1.1. Составьте и упорядочите по слоям сетевой график производства работ. Номера этапов необходимо обвести кружками, а операции  обозначить стрелками, проставляя над ними продолжительность обозначить стрелками, проставляя над ними продолжительность  операции. операции.
|

| 
| ||
| 1→2 | 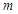
| ||
| 1→3 | |||
| 1→4 | 
| ||
| 2→3 | |||
| 2→6 | |||
| 4→3 | |||
| 4→6 | |||
| 3→5 | 15.1.2. Считая, что начало работы происходит во время 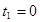 , определите время , определите время 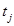 окончания каждого окончания каждого 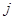 -го этапа и проставьте его над соответствующим кружком. -го этапа и проставьте его над соответствующим кружком.
| ||
| 3→7 | 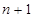
| ||
| 5→9 | 
| ||
| 6→7 | |||
| 6→8 | |||
| 7→8 | |||
| 7→9 | 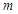
| ||
| 7→10 | |||
| 8→10 | |||
| 9→10 | 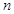
|
|
|
|
15.1.3. Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути.
15.1.4. Для каждой некритической операции  определите резервы свободного времени
определите резервы свободного времени 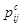 и проставьте их над стрелками рядом с
и проставьте их над стрелками рядом с  в скобках.
в скобках.
15.1.5. Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени 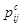 необходимо также найти полные резервы времени
необходимо также найти полные резервы времени 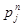 для каждого этапа.)
для каждого этапа.)
|
|
|


