Создание съёмочного обоснования по способу засечек проф. А.И. Дурнева.

Сущность метода заключается в следующем. Одновременно с прокладкой разомкнутого теодолитного хода TABCDEFG между исходным сторонами ТА и FA, опирающегося обоими концами на исходные пункты А и F, вправо и влево от направления хода, прямыми засечками определяют дополнительные пункты N₁, N_2…….. N_n  и М₁, М₂……, М _n.

 

 

 

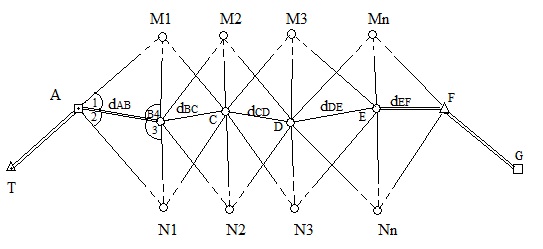
Важным здесь является то, что в таком построении измеряются только первая сторона d_AB и последняя d_EF (для контроля). Такой ход иногда называют угломерным. Углы измеряют круговыми приёмами- теодолитом типа Т5- одним приемом, а теодолитом Т30 -2мя приёмами с приставкой лимба между приемами на 90⁰. Длины сторон такого построения 250-350 м. углы не должны выходить за предел 30⁰-120⁰.

Контрольная обработка

1. По измеренной стороне d_AB и углам 1,4 и2,3 решением треугольников AM₁B по AN₁B теореме синусов вычисляют стороны ВМ₁ и В N₁:

 

                     ВМ₁= 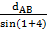,     В N₁=                                 ()

 

 

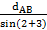
Далее решением треугольников BM₁C  и  В N₁C дважды вычисляют сторону теодолитного хода d_BC. если разность этих значений не превышает допуска 1/N (где N - знаменатель относительной ошибки), за результат принимают среднее значение. Аналогичным образом вычисляют дважды линии d_CD, d_DE,  d_EF сравнивая вычисленное значение последней стороны хода d_EF  с измеренным, вычисляют невязку - f_d:

                               f_d=

Если:  , где S - число сторон хода, то стороны хода d_i-k  

исправляют поправками: 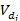= - , где L_i - удаление i-той стороны от исходного т.е. L_i=d₁+ d₂+ d_i-1.

2. Далее уравнивают упрощенным способом разомкнутый теодолитный ход (алгоритм см.) вычисляют координаты точек хода B,C,D,E.

3. Решением прямых геодезических засечек по формуле Юнга со сторон хода вычисляют координаты засекаемых точек M_i и N_i с контролем т.е. с двух сторон хода. При допустимых расхождениях за результат принимают средние координаты.

Несмотря на некоторое усложнение и увеличение объёма капиральных работ такое построение съёмочного обоснования имеет существенные  преимущества: 1. Способ позволяет с большей точностью и надёжностью создать съёмочное обосновании на полосе существенно шире, в три раза увеличить число пунктов обоснования. 2. При прокладке хода измеряются всего две стороны – первая и последняя. Важность этого решения в том, что существенно уменьшается объём линейных измерений (как более сложного процесса) кроме того такой угломерный ход может прокладываться в достаточно пересечённой местности.

Возможен и другой вариант такого вида построения.

 

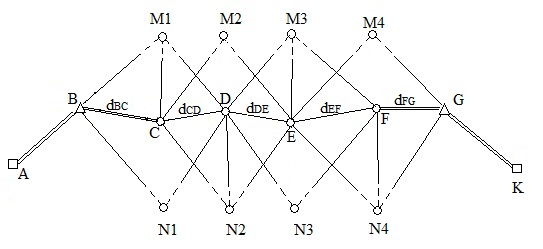
Он обусловлен отсутствием видимости по направлениям типа CN_1,  DM₂, EN₃  и др. Принципиальным отличием капиральной обработки измерений этого построения является то, что неизмеренные стороны теодолитного хода вычисляются только с одного треугольника. Кроме того, координаты засекаемых пунктов N1, M2, N3, M4 определяются также прямыми угловыми засечками, по дирекционным углам – по формулам Гаусса.

Построение планового съёмочного обоснования                  четырёхугольниками без диагоналей (сеть Зубрицкого).

       Идея построения предложена профессором Зурбрицким. Геометрическая сущность построения состоит в том, что оно состоит из четырёхугольников (без диагоналей), примыкающих один к другому. В каждом четырёхугольнике измеряют все четыре угла и одну сторону. Для решения четырёхугольников и контроля, в первом и последнем в сети измеряют длины двух смежных сторон (см. рис). Измеренные в сети стороны показаны двойной линией. Концы системы четырёхугольников привязывают к исходной геодезической основе.

       Метод построения съёмочного обоснования удобен в закрытых лесных районах с просеками, в населённых пунктах, при съёмках речных долин, больших по площади садах, питомниках, разбитых на кварталы и т. п. где измерения длин ходов теодолитных ходов существенно затрудняется. Построение может быть построено в виде звена четырёхугольников, сдвоенных звеньев и др. Чтобы достичь наибольшую точность вычисленных сторон,, необходимо при проектировании и закладке пунктов сети стремиться к тому, чтобы четырёхугольники были близки по форме к квадрату.

       Алгоритм уравнивания такой сети включает:

1. Вычисляют угловые невязки каждого четырёхугольника

            

Невязки не должны превышать 1,7'. Невязки распределяют между всеми четырьмя углами поровну. На центральных пунктах – в которых соприкасаются четыре четырёхугольника возникает условие горизонта. Сумма углов должна быть равна 360⁰. Невязки горизонтов также не должны превышать 1,7'. Невязку распределяют между углами данного горизонта поровну:               

                     

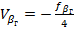
Чтобы не нарушались геометрические условия фигур, четырёхугольников, примыкающих к данному і-тому горизонту в остальные три угла каждого из них вводят поправки (вторичные) с противоположным знаком равным 1/3 .

2. Вычисляют исправленные углы четырёхугольников введением суммарных поправок (первичных и вторичных). Далее по формулам косекантов вычисляют стороны четырёхугольников сообразно с обозначениями на отдельном рис.:

  

 

  c= ,

  d= .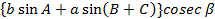

 

Решать четырёхугольники начинают с того, у которого измерены или вычислены две стороны.

       Координаты вершин четырёхугольников вычисляют составлением уравниванием одиночных разомкнутых ходов. Например для схемы на рис. первый ход:

 

 

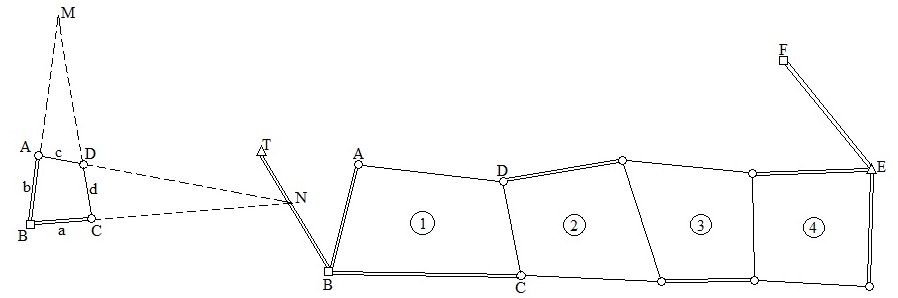
Рис. К решению четырёхугольников.                      Рис. Звено четырёхугольников без                             

диагональных привязок к                                                     геодезической поверхности.

 

На рисунках двойными линиями показаны измеренные, а одинарной измеренные стороны четырёхугольников. Известно, чтобы решить четырехугольник в нём должны быть измерены две стороны и три угла. Вычисление сторон начинают с с четырёхугольника в котором измерены все углы и две стороны – ABCD.

       Продолженные стороны  BA и CD, AD и BC пересекаются в точках M и N соответственно. Из треугольника BMC по теореме синусов можем написать:

              b+AM=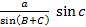

откуда:

               АМ=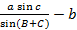

из треугольника AMD будем иметь:

                c=                                                            (  )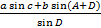

Аналогично для d будем иметь:

                 d=                                                            (  )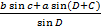

Таким образом в основу вычисления двух неизвестных сторон четырёхугольника положена теорема синусов решения косоугольного треугольника.

Правило: Если в четырёхугольнике без диагоналей известны две смежные стороны а и b и все четыре угла, то стороны c и d вычисляют по правилу: определяемая сторона равна дроби, числитель которой равен произведению противолежащей известной стороны, на синус угла между этой известной и соседней неизвестной сторонами, плюс произведение второй известной стороны на синус суммы углов, прилегающих к определяемой стороне, а знаменатель равен синусу угла между неизвестными сторонами, т.е.:

c= 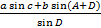 ,      d=  .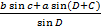

Способ применяют при создании съёмочного обоснования топографической съёмки широких долин рек со склонами при съёмках открытых пойм. Разбиваемый по берегу ход можно принять за теодолитный, но длины сторон в нем не измеряют за исключением первой и последней. Остальные стороны вычисляют решением треугольников по теореме синусов. Это одно из важных преимуществ. Кроме того, одновременно с вычислением сторон хода d_i  и координат точек хода определяют дополнительно координаты ряда съёмочных точек  M1,M2,…..N1,N2,… число которых в в двое превышает число точек. По существу его можно назвать угломерным ходом.

                                                    

 

                                                                            

 

 

                             

 

 

 

                    

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: