|
Методы расчета неблокирующих коммутационных систем
|
|
|
|
Методические указания
К выполнению заданий на практических занятиях
По дисциплине
«Теория телетрафика»
для студентов дневной формы обучения направления подготовки
11.03.02 «Инфокоммуникационные технологии и системы связи»
Саратов, 2018
Методические указания по решению задач
На практических занятиях и контрольных работах
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Студенты дневного отделения приступают к выполнению каждой задачи по порядку, начиная с задания 1, отчитываясь по решению письменно, сдавая каждую решенную задачу преподавателю.
КОНТРОЛЬНАЯ РАБОТА
Общие указания и выбор варианта
Контрольная работа (КTР) предназначена для развития навыков студентов заочной и заочно-сокращенной форм обучения по решению конкретных практических вопросов на основе полученных знаний при изучении курса. Одновременно выполнение КTР способствует более глубокому усвоению материала, связанного с задачами курса.
Перед выполнением каждой задачи необходимо изучить ту часть курса, которая относится к этой задаче. Выполнять задачи нужно вдумчиво и уметь обосновывать полученный результат. На защите проводится собеседование по выполненным работам.
Каждый студент выполняет семь задач в одном варианте. Номер варианта выбирается по порядку записи в журнале группы, поочередно (для студентов заочно-сокращенной формы обучения после окончания вариантов в таблице перейти в начало списка).
Требования к оформлению
При выполнении и оформлении КTР следует иметь в виду, что решения задач следует располагать в порядке номеров, указанных в заданиях, перед решением каждой задачи необходимо написать условие задачи для требуемого варианта. Каждый студент должен выполнить КTР в одном варианте, причем номер варианта должен соответствовать тем указаниям, которые имеются в контрольных заданиях. КTР, выполненные не по требуемому варианту, не зачитываются. Решения задач должны быть четкими, пояснения краткими, но без сокращения слов. В случае необходимости нужно делать ссылки на теорию, указывая учебник, автора, год издания, страницу и если необходимо, номер чертежа.
|
|
|
Все чертежи, рисунки, таблицы должны быть пронумерованы.
Расчетные формулы следует приводить в тексте работы в общем виде с объяснением входящих в них буквенных значений. Все числовые значения необходимо представить только в основных единицах (вольт, ампер и т.д.).
КTР, выполненные небрежно, без промежуточных вычислений, с пропуском задач, возвращаются студенту обратно для переработки.
В конце каждой КTР необходимо указать учебники и учебные пособия, которыми пользовался студент.
После выполнения и оформления КTР должна быть представлена преподавателю. Без зачтенных работ студент к сдаче зачета/экзамена не допускается.
Пояснения к выполнению заданий
Системы связи как системы массового обслуживания
Главными вопросами, которые следует уяснить при изучении данных вопросов - потоки вызовов и время обслуживания, являются: определение потока вызовов детерминированного и случайного потоков; способы задания потоков; их классификация с точки зрения стационарности, ординарности и последействия; основные характеристики потоков - интенсивность и параметр. Особое внимание следует обратить на формулы (распределения) Пуассона и Бернулли, описывающие вероятностные процессы в простейшем и примитивном потоках, которые в основном применяются в качестве математических моделей для реальных потоков вызовов, действующих на сетях связи. Следует обратить внимание на возможный характер распределения длительности обслуживания. Материал этих частей изложен на с. 14-34 [I].
|
|
|
Далее необходимо усвоить формулу нагрузки, расчет основных параметров нагрузки, единицы измерения нагрузки и интенсивности нагрузки, уяснить понятие поступающая, обслуженная, потерянная нагрузка, пропускная способность коммутационной системы. Вопрос о качестве обслуживания целесообразно рассматривать с учетом дисциплины обслуживания (по системе с явными потерями и по системе с ожиданием). Надо также уяснить, из каких элементов состоит математическая модель системы распределения информации, что такое дисциплина обслуживания, задачи теории телетрафика и методы их решения.
Ответы на вопросы изложены на с.6-13 и 34-50 [I].
Для закрепления материала раздела рекомендуется ответить на следующие вопросы.
1. Задачи теории телетрафика и методы их решения.
2. Потоки вызовов. Способы их задания. Стационарность, ординарность, последействие потока.
3. Основные характеристики потоков: интенсивность и параметр потока.
4. Простейший поток. Формула Пуассона.
5. Примитивный поток. Формула Бернулли.
6. Телефонная нагрузка и ее параметры, интенсивность нагрузки. Поступающая, обслуженная и потерянная нагрузка.
7. Колеблемость нагрузки во времени. Час наибольшей нагрузки. Коэффициент концентрации.
8. Единицы измерения нагрузки и интенсивность нагрузки.
9. Параметры нагрузки. Расчет возникающей нагрузки.
10. Понятие о потерях, типы потерь, нормы потерь.
11. Способы обслуживания потоков нагрузки. Качественные характеристики систем с явными потерями и с ожиданием.
12. Пропускная способность и среднее использование линий пучка.
МЕТОДЫ РАСЧЕТА НЕБЛОКИРУЮЩИХ КОММУТАЦИОННЫХ СИСТЕМ
При изучении этой части следует вспомнить основные характеристики простейшего и примитивного потоков, затем разобраться в методике составления уравнений состояния полнодоступного пучка линий при обслуживании указанных потоков и, наконец, проанализировать конечные результаты решения этих уравнений - формулу Эрланга и формулу Энгсета. Надо уметь пользоваться формулами Эрланга и Энгсета и таблицами, составленными по этим формулам.
|
|
|
Материал части раздела изложен на с.50-78 [ I ].
Во второй части раздела рассматриваются вопросы обслуживания вызовов полнодоступным пучком в системах с ожиданием. При изучении материала этой части раздела следует обратить внимание на то, что выбор метода расчета полнодоступного пучка при обслуживании простейшего потока по системе с ожиданием зависит от закона распределения длительности занятия линий пучка: при экспоненциальном распределении длительности занятия процесс обслуживания описывается второй формулой Эрланга, а при постоянной длительности занятия - формулой Кроммелина или Берка. Надо уметь определять основные качественные показатели работы устройств, обслуживающих вызовы по системе с ожиданием: вероятность ожидания сверх допустимого времени и среднее время ожидания задержанных вызовов.
Материал второй части раздела изложен на с.79-98 [I].
В третьей части раздела рассматриваются системы с повторными вызовами. Здесь следует обратить внимание на изменение величины поступающей нагрузки в зависимости от интенсивности повторных вызовов и на закономерности изменения характеристик качества обслуживания (потерь сообщения и среднего числа повторных вызовов) от величины использования линий в пучке и вероятности повторного вызова.
Материал третьей части изложен на с.98-1-6 [I].
При проработке материала четвертой части раздела (" Неполнодоступный пучок. Система с потерями ") следует усвоить способы построения ступенчатых и равномерных неполнодоступных включений и знать их параметры (доступность, емкость пучка линий, число нагрузочных групп). Надо знать приближенные методы расчета пропускной способности неполнодоступных включений. Особое внимание следует уделить методу О'Делла, получившему широкое применение в инженерной практике.
По четвертой части раздела рекомендуется изучить материал, изложенный на с.116-140[I].
Материал пятой части раздела в рекомендуемой литературе отсутствует, поэтому кратко он будет изложен на лекциях.
|
|
|
Для закрепления материала раздела рекомендуется ответить на следующие вопросы:
1. Структура пучков линий (полнодоступное и неполнодоступное включение).
2. Формула Эрланга для полнодоступного пучка с потерями. Область ее применения.
3. Расчет потерь в полнодоступных пучках при примитивном потоке вызовов. Формула Энгсета.
4. Характер зависимости использования линий в полнодоступном пучке от числа линий в пучке и потерь сообщения.
5. Характер зависимости использования линий в полнодоступном пучке от числа линий в пучке и числа источников нагрузки.
6. Формула для вероятности ожидания Р (g >0) при экспоненциальном распределении длительности занятия (вторая формула Эрланга).
7. Вероятность ожидания свыше определенного времени Р (g >t) и среднее время ожидани при экспоненциальном распределении длительности занятия
8. Вероятность Р (g >t) и среднее время ожидания при постоянной длительности занятия (кривые Кроммелина и Берка).
9. Типы неполнодоступных включений (ступенчатое и равномерное) и условия их применения.
10. Ступенчатое включение, выбор его структуры.
11. Равномерное неполнодоступное включение, выбор его структуры.
12. Методы расчета числа линий в неполнодоступном включении.
13. Характер зависимости использования линий в неполнодоступном пучке от числа линий в пучке и доступности при фиксированных потерях
Ниже приводятся задания для решения задач и рекомендации по их выполнению.
СОДЕРЖАНИЕ ЗАДАЧ
Задание 1
Задача 1. На коммутационную систему поступает поток вызовов, создающий нагрузку Y Эрланг. Определить вероятности поступления ровно i вызовов Pi (i=0, 1, 2...N) при примитивном потоке от N источников и Pi (i=0,1, 2...j...) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi =f (i) и произвести сравнение полученных результатов. Величины Y и N приведены в табл. 1.
Таблица 1
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y, эрл | 1,8 | 2,4 | 4,0 | 3,6 | 3,6 | 2,1 | 2,8 | 2,8 | 4,5 |
| N | 5 | 6 | 10 | 8 | 9 | 6 | 8 | 7 | 9 |
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Y, эрл | 1,5 | 2,0 | 1,8 | 3,2 | 5,0 | 2,1 | 4,7 | 4,3 | 3,5 | 4,5 |
| N | 5 | 5 | 6 | 8 | 10 | 7 | 10 | 10 | 7 | 10 |
Задание 2
Задача 2. Пучок ИШК координатной станции типа АТСК -Y обслуживает абонентов одного блока АИ. Определить поступающую на этот пучок нагрузку Y, если число абонентов, включенных в блок, N=1000, среднее число вызовов от одного абонента С, среднее время разговора Т, доля вызовов закончившихся разговором PP. значения с, Т и PP приведены в таблице 2. нумерация на сети пяти- или шестизначная.
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| c, выз/час | 2,0 | 2,2 | 2,7 | 3,0 | 2,5 | 2,4 | 2,3 | 2,8 | 2,0 |
| T, c | 140 | 130 | 120 | 100 | 110 | 130 | 140 | 120 | 140 |
| PP | 0,6 | 0,7 | 0,65 | 0,6 | 0,7 | 0,55 | 0,6 | 0,6 | 0,7 |
Таблица 2.
|
|
|
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| c, выз/час | 2,5 | 3,1 | 3,3 | 2,6 | 2,9 | 2,1 | 2,5 | 3,0 | 3,5 | 2,5 |
| T, c | 140 | 110 | 100 | 120 | 130 | 140 | 120 | 110 | 90 | 130 |
| PP | 0,55 | 0,55 | 0,50 | 0,6 | 0,5 | 0,6 | 0,65 | 0,6 | 0,7 | 0,6 |
Задание 3
Задача 3. Полнодоступный пучок из V линий обслуживает поток вызовов. Определить пропускную способность пучка, т.е. нагрузку Y, которая может поступать на этот пучок при заданной величине потерь по вызовам PВ в случае простейшего потока и примитивного потока от N1 и N2 источников. Значения V, PB, N1 и N2 приведены в таблице 3. По результатам расчета сделать выводы.
Таблица 3
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V | 4 | 5 | 6 | 8 | 7 | 5 | 6 | 7 | 8 |
| PB,%0 | 5 | 1 | 3 | 3 | 6 | 2 | 1 | 4 | 2 |
| N1 | 20 | 20 | 40 | 40 | 40 | 20 | 40 | 40 | 40 |
| N2 | 10 | 10 | 20 | 20 | 20 | 10 | 20 | 20 | 20 |
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| V | 4 | 5 | 7 | 9 | 8 | 5 | 6 | 8 | 7 | 5 |
| PB,%0 | 10 | 3 | 2 | 2 | 3 | 4 | 2 | 2 | 2 | 5 |
| N1 | 20 | 20 | 50 | 50 | 50 | 20 | 40 | 50 | 40 | 20 |
| N2 | 10 | 10 | 20 | 40 | 20 | 10 | 20 | 20 | 20 | 10 |
Задание 4
Задача 4. На коммутационный блок координатной станции типа АТСК поступает простейший поток вызовов, который создает нагрузку Yб эрланг при средней длительности занятия входа блока tб . Блок обслуживается одним маркером, работающим в режиме с условными потерями при постоянной длительности занятия tм. Блок обслуживается одним маркером, работающем в режиме с условными потерями при постоянной длительности занятия tм.
Задержанные вызовы обслуживаются в случайном порядке независимо от очередности поступления.
Определить вероятность ожидания свыше допустимого времени tд и среднее время ожидания задержанных вызовов tз. Значения Yб, tб, tм и tд.приведены в табл. 4.
Таблица 4
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Yб, эрл | 40 | 35 | 45 | 15 | 20 | 24 | 25 | 36 | 48 |
| tб,с | 80 | 70 | 90 | 90 | 60 | 48 | 75 | 72 | 96 |
| tм,с | 0,7 | 0,6 | 0,8 | 1,2 | 0,9 | 0,2 | 0,9 | 0,6 | 0,7 |
| tд ,с | 1,75 | 1,8 | 3,2 | 2,4 | 3,6 | 0,3 | 1,8 | 2,4 | 2,1 |
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Yб, эрл | 40 | 30 | 12 | 20 | 20 | 24 | 16 | 15 | 40 | 30 |
| tм, с | 80 | 60 | 96 | 80 | 60 | 48 | 80 | 60 | 80 | 90 |
| tм, с | 0,8 | 0,5 | 1,2 | 0,8 | 0,9 | 0,4 | 0,5 | 0,6 | 0,6 | 0,9 |
| tд,с | 2,4 | 1,0 | 1,8 | 1,6 | 2,7 | 0,8 | 0,5 | 1,2 | 1,8 | 2,7 |
Задание 5
Задача 5. Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью KBq при потерях P=0,005. Нагрузка на один вход ступени а, нагрузка в направлении y. Определить методом эффективной доступности емкость пучка V при установке на ступени блоков 60х80х400 и 80х120х400. Сравнить полученные результаты. Величины KBq, y, a приведены в таблице 5.
Таблица 5
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| KBq | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| y, Эрл | 30 | 40 | 35 | 45 | 25 | 32 | 23 | 20 | 28 |
| а, Эрл | 0,40 | 0,42 | 0,45 | 0,47 | 0,50 | 0,41 | 0,43 | 0,46 | 0,48 |
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| KBq | 20 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 |
| y, Эрл | 33 | 45 | 50 | 50 | 55 | 65 | 70 | 53 | 60 | 50 |
| а, Эрл | 0,49 | 0,60 | 0,65 | 0,62 | 0,67 | 0,7 | 0,61 | 0,63 | 0,66 | 0,68 |
Задание 6
Задача 6. На вход ступени ГИ АТС поступает нагрузка по двум пучкам линий, математическое ожидание которой Y1 и Y2. На выходе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам Ki . определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам расчета сделать вывод. Исходные данные приведены в табл.6.
Таблица 6
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y1, Эрл. | 35 | 30 | 50 | 65 | 45 | 20 | 33 | 26 | 31 |
| Y2, Эрл. | 25 | 60 | 25 | 15 | 30 | 60 | 57 | 24 | 39 |
| K1 | 0,2 | 0,15 | 0,1 | 0,2 | 0,25 | 0,1 | 0,1 | 0,12 | 0,1 |
| K2 | 0,3 | 0,2 | 0,15 | 0,2 | 0,35 | 0,15 | 0,17 | 0,34 | 0,35 |
| K3 | 0,5 | 0,25 | 0,3 | 0,25 | 0,4 | 0,25 | 0,27 | 0,54 | 0,55 |
| K4 | - | 0,4 | 0,45 | 0,35 | - | 0,5 | 0,46 | - | - |
| Номер варианта | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Y1, Эрл. | 20 | 40 | 45 | 25 | 40 | 70 | 48 | 17 | 42 | 51 |
| Y2, Эрл. | 30 | 45 | 25 | 50 | 40 | 30 | 37 | 23 | 28 | 29 |
| K1 | 0,1 | 0,2 | 0,15 | 0,1 | 0,15 | 0,1 | 0,13 | 0,15 | 0,1 | 0,1 |
| K2 | 0,2 | 0,35 | 0,2 | 0,25 | 0,25 | 0,15 | 0,20 | 0,35 | 0,3 | 0,15 |
| K3 | 0,3 | 0,45 | 0,3 | 0,3 | 0,6 | 0,35 | 0,27 | 0,5 | 0,6 | 0,3 |
| K4 | 0,4 | - | 0,35 | 0,35 | - | 0,4 | 0,4 | - | - | 0,45 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Решение задачи 1 имеет своей целью закрепление материала по изучению математических моделей простейшего и примитивного потоков вызовов. К ее выполнению можно приступить после проработки первой части раздела программы.
Вероятностный процесс поступления вызовов простейшего потока описывается формулой (распределения) Пуассона:
 а примитивного - распределение Бернулли:
а примитивного - распределение Бернулли:
 где а=
где а=  - нагрузка, поступающая от одного источника.
Примитивный поток создается конечным числом источников, а простейший - теоретически бесконечным числом источников вызовов (практически достаточно, чтобы N было больше 100). Расчет распределения Пуассона и Бернулли целесообразно вести в следующей последовательности. Сначала, полагая i=0, определяют вероятность отсутствия вызовов Р0. Остальные Рi находят по рекуррентным формулам: - нагрузка, поступающая от одного источника.
Примитивный поток создается конечным числом источников, а простейший - теоретически бесконечным числом источников вызовов (практически достаточно, чтобы N было больше 100). Расчет распределения Пуассона и Бернулли целесообразно вести в следующей последовательности. Сначала, полагая i=0, определяют вероятность отсутствия вызовов Р0. Остальные Рi находят по рекуррентным формулам:
 ; (j=0, 1, 2...) - для простейшего потока, ; (j=0, 1, 2...) - для простейшего потока,
 ; (j=0, 1, 2...) - для примитивного потока,
где j+1=i.
Максимальное значение i при расчете Рi для простейшего потока принять равной заданному N для примитивного потока.
Вторая задача выполняется после изучения третьей части первого раздела программы. Основная цель решения этой задачи заключается в приобретении практических навыков по расчету возникающей нагрузки. Так как по условию задачи из всех возможных исходов, которыми может закончиться поступивший вызов, задана только доля состоявшихся разговоров РР, то расчет нагрузки выполняется по формуле, в которой непроизводительная нагрузка учитывается коэффициентом a: формула (3.13) с.44[1].
Значения величин, входящих в эту формулу, приведены на с.42 [1].Коэффициент a определяется по графику, приведенному в этой же литературе. Надо помнить, что в результате расчета нагрузка получается в эрлангах, если время занятия задано в часах.
Задача 3 выполняется после изучения первой части второго раздела программы. Решение этой задачи преследует цель показать зависимость пропускной способности полнодоступного пучка линий от характера (класса) поступающего потока вызовов.
Обслуживание полнодоступным пучком простейшего потока описывается первой формулой Эрланга: формула (4.28) в [1], а примитивного потока - формулой Энгсета: (4.38)по причине сложности расчета пропускной способности по формулам Эрланга и Энгсета (они не решаются относительно y) рекомендуется пользоваться таблицами Пальма [4] (приложение 3) для простейшего потока (табулированная формула Эрланга), что касается таблиц формулы Энгсета, то они встречаются реже. Поэтому в приложениях 1 и 2 данного УМД приведены соответственно значения функций Эрланга и Энгсета, необходимые для решения этой задачи.
Заметим, что здесь, как в первой задаче y=l для простейшего потока и y=aN для примитивного потока, где а- нагрузка, поступающая от одного источника.
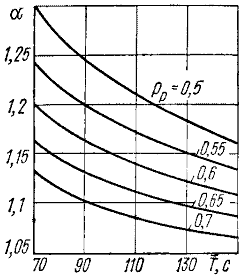
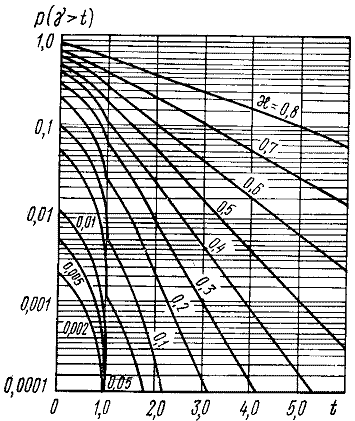
Задачу 4 задания1 рекомендуется решить после изучения второй части раздела 2 программы. Решение задачи 4 поможет приобрести навык по определению основных качественных показателей работы приборов управления КАТС.
Исследование систем, работающих в режиме маркеров КАТС, проведено Берком. С помощью полученных им формул построены кривые, которые приведены на рис.1 и 2 приложения 3 УМД. Эти кривые дают возможность легко определить значения требуемых величин: вероятность ожидания свыше времени t, т.е. Р (g >t) и среднее время ожидания tз=tm*g з в зависимости от нагрузки на маркер ; (j=0, 1, 2...) - для примитивного потока,
где j+1=i.
Максимальное значение i при расчете Рi для простейшего потока принять равной заданному N для примитивного потока.
Вторая задача выполняется после изучения третьей части первого раздела программы. Основная цель решения этой задачи заключается в приобретении практических навыков по расчету возникающей нагрузки. Так как по условию задачи из всех возможных исходов, которыми может закончиться поступивший вызов, задана только доля состоявшихся разговоров РР, то расчет нагрузки выполняется по формуле, в которой непроизводительная нагрузка учитывается коэффициентом a: формула (3.13) с.44[1].
Значения величин, входящих в эту формулу, приведены на с.42 [1].Коэффициент a определяется по графику, приведенному в этой же литературе. Надо помнить, что в результате расчета нагрузка получается в эрлангах, если время занятия задано в часах.
Задача 3 выполняется после изучения первой части второго раздела программы. Решение этой задачи преследует цель показать зависимость пропускной способности полнодоступного пучка линий от характера (класса) поступающего потока вызовов.
Обслуживание полнодоступным пучком простейшего потока описывается первой формулой Эрланга: формула (4.28) в [1], а примитивного потока - формулой Энгсета: (4.38)по причине сложности расчета пропускной способности по формулам Эрланга и Энгсета (они не решаются относительно y) рекомендуется пользоваться таблицами Пальма [4] (приложение 3) для простейшего потока (табулированная формула Эрланга), что касается таблиц формулы Энгсета, то они встречаются реже. Поэтому в приложениях 1 и 2 данного УМД приведены соответственно значения функций Эрланга и Энгсета, необходимые для решения этой задачи.
Заметим, что здесь, как в первой задаче y=l для простейшего потока и y=aN для примитивного потока, где а- нагрузка, поступающая от одного источника.
Задачу 4 задания1 рекомендуется решить после изучения второй части раздела 2 программы. Решение задачи 4 поможет приобрести навык по определению основных качественных показателей работы приборов управления КАТС.
Исследование систем, работающих в режиме маркеров КАТС, проведено Берком. С помощью полученных им формул построены кривые, которые приведены на рис.1 и 2 приложения 3 УМД. Эти кривые дают возможность легко определить значения требуемых величин: вероятность ожидания свыше времени t, т.е. Р (g >t) и среднее время ожидания tз=tm*g з в зависимости от нагрузки на маркер
 ;
где t= ;
где t= 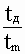 и g = и g = 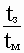 - время, измеренное в единицах длительности занятия.
Задачу 5 рекомендуется решить по методу эффективной доступности, изложенному на с. 152-156 в [1]. В приложении 4 и в [5] имеются таблицы коэффициентов a и b. Коэффициент Q принятый равным 0,7. Структурные параметры n A= 15, mA=kВ=20, f=1 блока 60х80х400 и nA=13,33, mA=kB=20, f=1блока 80х120х400.
Решить задачу 6 следует после изучения второй части раздела 4 программы.
Расчетная нагрузка учитывает колеблемость нагрузки. Поступающей на пучок соединительных устройств заданной емкости. Ее значение определяется по формуле (10.47) в [1].
По результатам расчета рекомендуется сделать вывод о величине относительного отклонения расчетной нагрузки от ее математического ожидания в зависимости от величины математического ожидания нагрузки
d i= - время, измеренное в единицах длительности занятия.
Задачу 5 рекомендуется решить по методу эффективной доступности, изложенному на с. 152-156 в [1]. В приложении 4 и в [5] имеются таблицы коэффициентов a и b. Коэффициент Q принятый равным 0,7. Структурные параметры n A= 15, mA=kВ=20, f=1 блока 60х80х400 и nA=13,33, mA=kB=20, f=1блока 80х120х400.
Решить задачу 6 следует после изучения второй части раздела 4 программы.
Расчетная нагрузка учитывает колеблемость нагрузки. Поступающей на пучок соединительных устройств заданной емкости. Ее значение определяется по формуле (10.47) в [1].
По результатам расчета рекомендуется сделать вывод о величине относительного отклонения расчетной нагрузки от ее математического ожидания в зависимости от величины математического ожидания нагрузки
d i=  ,
где Yi,p- расчетное значение нагрузки в направлении i.
Yi - среднее (математическое ожидание) в этом же направлении.
ПРИЛОЖЕНИЕ 1 ,
где Yi,p- расчетное значение нагрузки в направлении i.
Yi - среднее (математическое ожидание) в этом же направлении.
ПРИЛОЖЕНИЕ 1
 Значение функции Эрланга
Значение функции Эрланга
|
ПРИЛОЖЕНИЕ 2
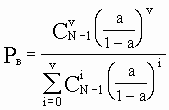
Значение функции Энгсета; N=const
| N=10 | ||
| V a | 4 | 5 |
| 0,09 | 0,005 | |
| 0,10 | 0,007 | |
| 0,11 | 0,010 | 0,001 |
| 0,12 | 0,014 | 0,002 |
| 0,13 | 0,018 | 0,003 |
| 0,14 | 0,023 | 0,004 |
| 0,15 | 0,028 | 0,005 |
|
| ||||||
a | 4 | 5 | 6 | 7 | 8 | |
| 0,04 | 0,005 | 0,001 | ||||
| 0,05 | 0,011 | 0,002 | ||||
| 0,06 | 0,020 | 0,004 | ||||
| 0,07 | 0,007 | 0,001 | ||||
| 0,08 | 0,002 | |||||
| 0,09 | 0,004 | 0,001 | ||||
| 0,10 | 0,007 | 0,001 | ||||
| 0,11 | 0,010 | 0,002 | ||||
| 0,12 | 0,004 | 0,001 | ||||
| 0,13 | 0,006 | 0,001 | ||||
| 0,14 | 0,002 | |||||
| 0,15 | 0,003 | |||||
| N=40 | ||||
| V a | 6 | 7 | 8 | 9 |
| 0,03 | 0,001 | |||
| 0,04 | 0,003 | |||
| 0,05 | 0,009 | 0,002 | ||
| 0,06 | 0,006 | 0,001 | ||
| 0,07 | 0,012 | 0,004 | 0,001 | |
| 0,08 | 0,008 | 0,002 | ||
| 0,09 | 0,005 | |||
| 0,10 | 0,009 | |||
| N=50 | |||
| V a | 7 | 8 | 9 |
| 0,04 | 0,002 | ||
| 0,05 | 0,008 | 0,002 | |
| 0,06 | 0,018 | 0,006 | 0,002 |
| 0,07 | 0,013 | 0,004 | |
| 0,08 | 0,010 | ||
ПРИЛОЖЕНИЕ 3