 |
Расчет линейной цепи постоянного тока методом пропорциональных величин
|
|
|
|
Содержание
1.Краткие теоретические сведения
Элементы электрической цепи постоянного тока.
Принцип линейности
Особенности расчета лестничной цепи
Расчет цепи методом пропорциональных величин
2. Задание на расчет
3. Примеры расчета лестничной цепи
Пример расчета при заданном воздействии на входе
Пример расчета при заданном напряжении или токе на резисторе
4. Контрольные вопросы
1. Краткие теоретические сведения
Элементы электрической цепи постоянного тока.
Электрической цепью (ЭЦ) называется совокупность электропроводящих устройств, электромагнитные процессы в которых можно описать с помощью понятий напряжения и тока.
Линейной называют ЭЦ, параметры элементов которой не зависят от тока или напряжения.
Линейная ЭЦ постоянного тока состоит из трех основных элементов, получивших названия: резистор, идеальный источник напряжения и идеальный источник тока. Табл. 1 показывает определения, формулы и условные обозначения этих элементов: сверху отечественное, снизу европейское.
Табл.1. Определения, формулы и условные обозначения элементов цепи постоянного тока.
| Название | Определение | Условное обозначение | Формула |
| Резистор (идеальный) | Идеализированный элемент ЭЦ, характеризующийся определенной зависимостью между током и напряжением | 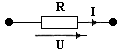
|
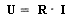
|
| Идеальный источник напряжения | Идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от тока и равно заданной величине E, называемой задающим напряжением или ЭДС. | 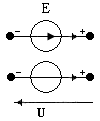
|
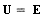
|
| Идеальный источник тока. | Идеализированный элемент ЭЦ, ток которого не зависит от напряжения на зажимах и равен заданной величине J, называемой задающим током. | 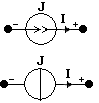
|

|
|
|
|
Принцип линейности
Воздействием будем называть задающее напряжение Е (ЭДС) или задающий ток J источника, рис.1а. Реакцией будем называть напряжение U или ток I в любом элементе ЭЦ, вызванные воздействием, рис.1б.
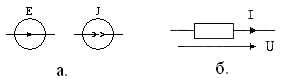
Рис.1. Графические изображения воздействия, рис.1а, и реакции цепи, рис.1б.
Принцип линейности: линейной сумме воздействий (на входе) соответствует та же самая линейная сумма реакций (на выходе) или:
· Сумме воздействий Е1 и Е2 будет соответствовать сумма реакций I1 и I2 на каждое из воздействий в отдельности, рис. 2.
· Увеличению воздействия Е в k раз будет соответствовать
увеличение реакции I также в k раз.

Рис.2. Иллюстрация принципа линейности
Особенности расчета лестничной цепи
Лестничной называют цепь, состоящую из чередующихся продольных и поперечных ветвей. Примером такой цепи может служить цепь согласно рис.2.
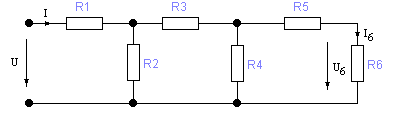
Рис 3. Пример лестничной цепи
Такую цепь можно представить как последовательность чередующихся делителей тока и напряжения, согласно рисункам 4а и 4б.
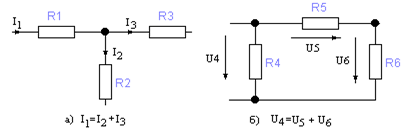
Рис. 4. Делитель тока (рис. 4а) и делитель напряжения (рис. 4б)
Для таких делителей всегда можно найти ток или напряжение предыдущей ветви через токи или напряжения двух последующих ветвей. Поэтому расчет цепи, т.е. нахождение всех токов или напряжений удобно делать, двигаясь от конца к началу цепи, т.е. от известной реакции к неизвестному воздействию. Практический интерес, однако, представляет собой обратная задача, т.е. расчет реакции по заданному воздействию. Для её решения используют метод пропорциональных величин.
Расчет цепи методом пропорциональных величин.
Расчетом цепи называют процесс нахождения напряжений и токов на всех её элементах
Расчет лестничной цепи ведется по этапам:
- задаются произвольно напряжением или током последней ветви лестничной цепи, условно присваивая ему величину, равную единице,
|
|
|
- затем, используя операции сложения и умножения на коэффициент, определяют все остальные токи и напряжения.
- полученную расчетом величину воздействия  сравнивают с заданной величиной
сравнивают с заданной величиной  и находят коэффициент преобразования
и находят коэффициент преобразования
К =  ,
,
-все рассчитанные величины токов и напряжений умножают на коэффициент преобразования К.
Преобразованные величины токов и напряжений согласно принципу линейности будут соответствовать заданному воздействию.
Проверяют правильность расчета, это можно сделать, пользуясь критерием выполнения баланса мощностей в цепи.
Для схемы, изображенной на рис.3, уравнение баланса мощностей выглядит так:
U×I=R1I12+ R2I22+ R3I32+ R4I42+ R5I52+ R6I62.
Уравнение гласит: Мощность, генерируемая источником напряжения U, равна сумме
мощностей, потребляемых резисторами R1 ÷ R6.
2. Задание
1. Используя заданные варианты схем и параметров рассчитать лестничную цепь, т.е. найти все токи и напряжения на элементах.
2. Проверить правильность расчета схемы с помощью уравнения баланса мощностей.
3. Собрать схему в среде EWB и проверить правильность расчета с помощью измерения тока и напряжения на заданном элементе.
4. Письменно ответить на контрольные вопросы
Варианты схем
В приведенных ниже вариантах схем основным является вариант 1, остальные можно привести к нему используя три преобразования, представленные на рис.5.
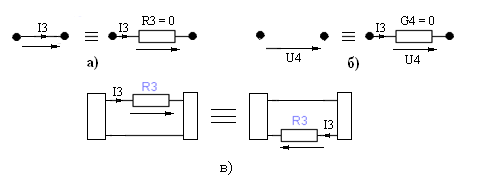
Рис.5. Эквивалентные преобразования элементов лестничной цепи:
- короткозамкнутую ветвь можно заменить обычной с сопротивлением, равным нулю (рис.5а),
- разомкнутую ветвь можно заменить обычной с проводимостью, равной нулю (рис.5б),
- расчет лестничной цепи не изменится, если в любом поперечном сечении резистор перенести из верхнего провода в нижний и поменять направления тока и напряжения (рис.5б).
Варианты:

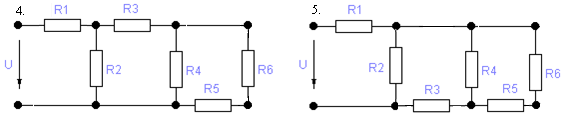

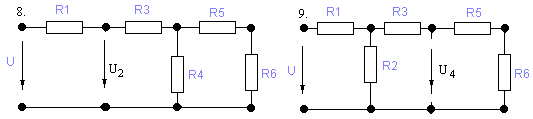
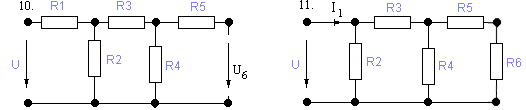
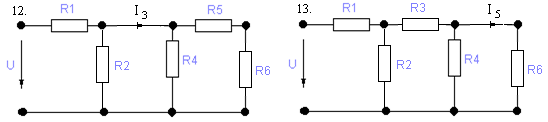
Варианты параметров элементов схемы
| № варианта | № схемы | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | Заданное значение |
| I6 = 1 A | ||||||||
| U5= 4 B | ||||||||
| I4= 2 A | ||||||||
| U3= 8 B | ||||||||
| I2= 4 A | ||||||||
| U1= 12 B | ||||||||
| U = 24 B | ||||||||
| ∞ | I = 8 A | |||||||
| ∞ | I1 = 8 A | |||||||
| ∞ | U2= 4B | |||||||
| I3= 4 A | ||||||||
| U5= 2 B | ||||||||
| I6 = 1 A | ||||||||
| U5= 2 B | ||||||||
| I3= 4 A | ||||||||
| U2= 4B | ||||||||
| I1 = 8 A | ||||||||
| I = 8 A | ||||||||
| U = 24 B | ||||||||
| U1= 12 B | ||||||||
| ∞ | I2= 4 A | |||||||
| ∞ | U3= 8 B | |||||||
| ∞ | I4= 2 A | |||||||
| U5= 4 B | ||||||||
| I6 = 1 A |
|
|
|
3. Примеры расчета лестничной цепи
Пример 1.
Задание: Рассчитать цепь постоянного тока со смешанным соединением резисторов методом пропорциональных величин.
Исходные данные:
| № варианта схемы | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | Заданное значение |
| U=18 B |
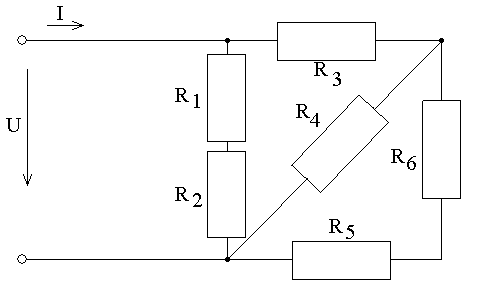
Решение
Предварительный расчет. Зададимся I6=1 А, после этого предварительный расчет токов и напряжений можно провести следуя движению по схеме от конца к началу:
I6 =1 А, I5 =I6 = 1 A
По закону Ома U5 = I5 ·R5 = 3 В Ома U6 = I6 ·R6 = 5 В
По второму закону Кирхгофа U4 = U5+ U6 =I6 (R5+R6) = 3+5 = 8 B
По закону Ома I4 = U4/R4 =  = 1 A
= 1 A
По первому закону Кирхгофа I3= (I4 + I5) = 1 + 1 = 2 А
По закону Ома U3 = I3 R3 = 2·2 = 4 B
По второму закону Кирхгофа U = U12 = U3 +U4 = 4 + 8 =12 B
По закону Ома I1 =I2 = U12/(R1+R2) =12/(9+1) = 1,2 А
По закону Ома U1 = I1R1 = 1,2·9 =10,8 В
По закону Ома U2 = I2R2 = 1,2·1 = 1,2 В
По первому закону Кирхгофа I = I1 + I3 = 1,2 + 2 = 3,2 А
Предварительный расчет окончен, его результаты можно записать таблицей
| На элементах | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | На входе |
| Ток I,А | 1,2 | 1,2 | 2 | 1 | 1 | 1 | I=3,2 |
| Напряжение U, В | 10,8 | 1,2 | 4 | 8 | 3 | 5 | U =12 |
Окончательный расчет. По расчету получилось U2 = 12 В, задано же U2 = 18 В. Коэффициент пересчета k=U2/ U2 =18/12=1,5. Все напряжения и токи предыдущей таблицы, т.е. найденные величины, умножаем на этот коэффициент, в итоге получаем таблицу результатов окончательного расчета.
|
|
|
| На элементах | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | На входе |
| Ток I,А | 1,8 | 1,8 | 1,5 | 1,5 | 1,5 | I=4,8 | |
| Напряжение U, В | 16,2 | 1,8 | 4,5 | 7,5 | U=18 |
Проверка. Проверяем правильность расчета с помощью уравнения баланса мощностей. Для нашей схемы оно выглядит так:
U×I=R1I12+ R2I22+ R3I32+ R4I42+ R5I52+ R6I62=
18×4,8=9× 1,82+1× 1,82+2× 32+8× 1,52+3× 1,52+5× 1,52
86,40=29,16+3,24+18+18+6,75+11,25=86,40
Полученное тождество подтверждает расчет и гласит: Мощность, генерируемая источником напряжения U, равна сумме мощностей, потребляемых резисторами R1 ÷ R6.
Проверка в среде EWB также подтверждает расчет. Если ко входу заданной цепи подключить источник напряжения 18 В, то ток в шестой ветви составит 1,5А.
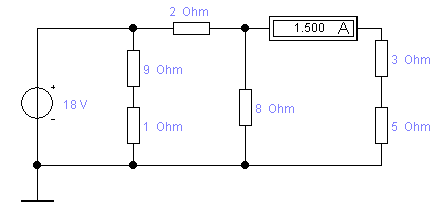
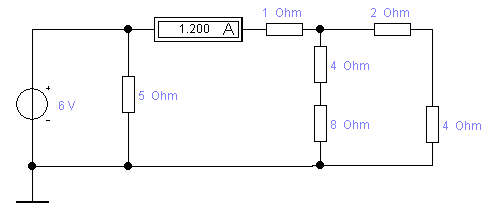
Пример 2
 Задание:
Задание:
Рассчитать цепь согласно
варианту. Дано:
R1 = 5 Ом
R2 = 1 Ом
R3 = 4 Ом
R4 = 8 Ом
R5 = 2 Ом
R6 = 4 Ом
I2 зад= 1.2 A
Решение:
Предварительный расчет. Зададимся I6=1 А, после этого предварительный расчет токов и напряжений можно провести следуя движению по схеме от конца к началу:
По закону Ома напряжение U6 =I6 R6=4В
Находим по схеме ток I5 =I6=1А.
По закону Ома напряжение U5= I5 R5=2В
Находим суммарное напряжение U34= U5+ U6=6В
R34 = 4+8 =12 Ом
По закону Ома ток I3 =I4= I34= U34 / R34 =6/12=0,5 A
По закону Ома напряжение U3= I3 R3 =2В
По закону Ома напряжение U4= I4 R4 =4В
По первому закону Кирхгофа ток I2= I3+ I5=1,5 А
По закону Ома напряжение U2= I2 R2 =1,5В
По второму закону Кирхгофа напряжение U1= U34+ U2=7,5В
Находим общее напряжение U=U1=7,5В
По закону Ома ток I1= U1 / R1=1,5 А
По первому закону Кирхгофа общий ток I= I1+ I2=3 А
Предварительный расчет окончен, его результаты можно записать таблицей
| На элементах | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | На входе |
| Ток I,А | 1,5 | 1,5 | О,5 | 0,.5 | 1 | 1 | I=3 |
| Напряжение U, В | 7,5 | 1,5 | 2 | 4 | 2 | 4 | U =7,5 |
Окончательный расчет. Предварительный расчет закончен и потому находим коэффициент преобразования
К=  =
= 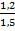 =0,8
=0,8
Полученные ранее величины умножаем на этот коэффициент, в итоге имеем результаты окончательного расчета
| На элементах | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | На входе |
| Ток I,А | 1,2 | 1,2 | О,4 | 0,.4 | 0,8 | 0,8 | I=2,4 |
| Напряжение U, В | 1,2 | 1,6 | 3,2 | 1,6 | 3,2 | U=6 |
Проверка
Проверяем правильность расчета с помощью уравнения баланса мощностей. Для нашей схемы оно выглядит так:
U×I=R1I12+ R2I22+ R3I32+ R4I42+ R5I52+ R6I62=
6×2,4=5× 1,22+1× 1,22+4× 0,42+8× 0,42+2× 0.82+4× 0,82
14,40=7,3+1,44+0,64+1,28+1,28+2,56=14,40
Полученное тождество подтверждает расчет и гласит: Мощность, генерируемая источником напряжения U, равна сумме мощностей, потребляемых резисторами R1 ÷ R6.
|
|
|
Проверка в среде EWB также подтверждает расчет. Если ко входу заданной цепи подключить источник напряжения 6 В, то ток во второй ветви составит 1,2А.
4.Контрольные вопросы
1. Как формулируется принцип линейности?
2. Какие два этапа определяют расчет методом пропорциональных величин?
3. Почему предварительный расчет цепи осуществляют, двигаясь от её конца к началу?
4. Если структура цепи будет отлична от лестничной, можно ли будет использовать метод пропорциональных величин?
5. Для проверки правильности расчета цепи можно использовать критерий выполнения законов Кирхгофа. Какие уравнения Вы бы использовали для этих целей?
|
|
|


