 |
Обработка результатов эксперимента при равномерном дублировании опытов
|
|
|
|
Министерство науки и высшего образования РФ
ФГБОУ ВО «Брянский государственный технический университет»
Кафедра «Триботехническое материаловедение и технологии материалов»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине
«Методы математического моделирования в машиностроении»
Вариант 1
Выполнил:
Студент группы З18-МАШ-ИРМ-Б
Зачетная книжка №1811.44
Котов В.В.
Проверил:
к.т.н., доцент
Шевелева Е.В.
Брянск 2020
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Брянский государственный технический университет»
Кафедра «Триботехническое материаловедение и технологии материалов»
ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ
по дисциплине: «МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
В МАШИНОСТРОЕНИИ»
Автор работы Котов В.В.
Группа З-18-МАШ-ИРМ-Б № зачетной книжки 1811.44
Содержание работы
Отчет по работе состоит из пояснительной записки, содержащей:
- титульный лист;
- введение;
- основную часть:
1) Получение линейной математической модели объектов исследований.
Задавшись математической моделью, провести обработку результатов исследования, проверить адекватность полученной математической модели, оценить характер и степень влияния каждого фактора на выходную величину. Все вычисления и полученные графики должны быть приведены в отчете.
|
|
|
2) Получение математической модели объектов исследований с помощью планов второго порядка.
Задавшись математической моделью, оценить значимость коэффициентов полученной модели и проверить адекватность модели. Все вычисления должны быть приведены в отчете.
- заключение;
- список использованной литературы.
 |
Введение
Математические модели являются инструментальным средством описания задач самого разного класса. Причем задачи из разных областей экономики могут иметь похожие модели и решаться одинаковыми методами. Использование корректно построенной модели какого-либо процесса позволяет формализовать и описать наиболее важные связи между объектами, оценить различные параметры зависимостей, предсказывать поведение объекта, тем самым определять наилучшие решения в той или иной ситуации, оценить количественно эффективность принимаемых решений, прогнозировать их негативные последствия, использовать полученные оценки.
Математическая модель – это условный совокупный образ объекта в виде совокупности уравнений, неравенств, логических соотношений, созданный для получения новых знаний, исследования объекта, анализа и оценки принимаемых решений в конкретных или возможных ситуациях.
Моделирование – это метод исследования объектов, процессов на их моделях, построения и изучения моделей, определения и улучшения их характеристик, рационализирующих способ построения и управления.
В каждой задаче мы должны ясно определить цели, поставленные перед системой, изучить обстановку, освоиться с терминологией, процессом, определить различные способы действия, приемлемые для ситуации, дать в какой-то форме постановку задачи. Построить подходящую логическую или математическую модель, которая свяжет переменные задачи с реальными ограничениями, целями задачи, мерой эффективности. Затем, исходя из полученной модели, выбрать метод и найти решение, оптимизирующее эту меру эффективности, т.е. оптимальное решение.
|
|
|
Задача №1
Получение линейной математической модели объектов исследования
Исходные данные вариант 1
| № опыта | Значения факторов | Результаты эксперимента, | ||||||
| x1 | x2 | x3 | у j1 | у j2 | у j3 | у j4 | у j5 | |
| 1 | 20 | 0 | 4 | 39 | 41 | 41 | 41 | 39 |
| 2 | 60 | 0 | 4 | 46 | 44 | 43 | 43 | 44 |
| 3 | 20 | 60 | 4 | 53 | 53 | 52 | 53 | 52 |
| 4 | 60 | 60 | 4 | 47 | 50 | 49 | 49 | 51 |
| 5 | 20 | 0 | 5 | 32 | 31 | 34 | 35 | 33 |
| 6 | 60 | 0 | 5 | 38 | 37 | 39 | 36 | 37 |
| 7 | 20 | 60 | 5 | 43 | 45 | 47 | 46 | 45 |
| 8 | 60 | 60 | 5 | 55 | 53 | 53 | 54 | 53 |
Обработка результатов эксперимента при равномерном дублировании опытов
В случае равномерного дублирования опытов результаты эксперимента обрабатываются в следующей последовательности.
1. Произведем вычисление средних арифметических выходных величин из каждой серии дублированных опытов из таблицы «вариант 1» по формуле 
j= 
результаты расчетов запишем во 2-й столбец таблицы (1).
j = (39+41+41+41+39):5 = 40,2 j = (46+44+43+43+44):5 = 44
j = (47+50+49+49+51):5 = 49,2 j = (53+53+52+53+52):5 = 52,6
j = (32+31+34+35+33):5 = 33 j = (38+37+39+36+37):5 = 37,4
j = (43+45+47+46+45) = 45,2 j = (55+53+53+54+53) = 53,6
| № Опыта | j
|  j
| S2j |
| 1 | 40,2 | ||
| 2 | 44 | ||
| 3 | 52,6 | ||
| 4 | 49,2 | ||
| 5 | 33 | ||
| 6 | 37,4 | ||
| 7 | 45,2 | ||
| 8 | 53,6 |
Таблица 1
2. Вычислим коэффициент регрессии для ПФП по формуле
b0= 
, знаки для вычисления берем из таблицы 2. В этой формуле вместо уj следует взять среднее значение j по каждой серии дублированных опытов.
| № опыта | Х 0 | Х 1 | Х 2 | Х 3 | Х 1 х 2 | Х 1 х 3 | Х 2 х 3 | у |
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | У1 |
| 2 | +1 | +1 | -1 | -1 | -1 | -1 | +1 | У2 |
| 3 | +1 | -1 | +1 | -1 | -1 | +1 | -1 | У3 |
| 4 | +1 | +1 | +1 | -1 | +1 | -1 | -1 | У4 |
| 5 | +1 | -1 | -1 | +1 | +1 | -1 | -1 | У5 |
| 6 | +1 | +1 | -1 | +1 | -1 | +1 | -1 | У6 |
| 7 | +1 | -1 | +1 | +1 | -1 | -1 | +1 | У7 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | У8 |
Таблица2
b0 = (40,2+44+52,6+49,2+33+37,4+45,2+53,6):8 = 44,4
b1 = (-40.2+44-52.6+49.2-33+37.4-45.2+53.6):8 = 1,65
b2 = (-40.2-44+52.6+49.2-33-37.4+45.2+53.6):8 = 5,75
b3 = (-40.2-44-52.6-49.2+33+37.4+45.2+53.6):8 = -2,1
b12 = (40,2-44-52,6+49,2+33-37,4-45,2+53,6):8 = -0,4
b13 = (40,2-44+52,6-49,2-33+37,4-45,2+53,6):8 = 1,55
|
|
|
b23 = (40,2+44-52,6-49,2-33-37,4+45,2+53,6):8 = 1,35
Запишем полученную математическую модель:
= 44,4 + 1,65х1 + 5,75х2 - 2,1х3 - 0,4х1х2 + 1,55х1х3 + 1,35х2х3
3. В полученное уравнение регрессии в нормализованных обозначениях факторов подставляем значения факторов x1, x2,…, xk, соответствующие условиям 1-го, 2-го, …, N-го опытов (N- число основных опытов плана, т.е. число серий дублированных опытов). Таким образом, вычисляем значения выходной величины 
1, 2, … N, предсказанные уравнением регрессии для каждого из опытов.
ŷ1 = 44,4 - 1,65 - 5,75 + 2,1 - 0,4 + 1,55 + 1,35 = 41,6
ŷ2 = 44,4 + 1,65 - 5,75 + 2,1 + 0,4 - 1,55 + 1,35 = 42,6
ŷ3 = 44,4 - 1,65 + 5,75 + 2,1 + 0,4 + 1,55 - 1,35 = 51,2
ŷ4 = 44,4 + 1,65 + 5,75 + 2,1 - 0,4 - 1,55 - 1,35 = 50,6
ŷ5 = 44,4 - 1,65 - 5,75 - 2,1 - 0,4 - 1,55 - 1,35 = 31,6
ŷ6 = 44,4 + 1,65 - 5,75 - 2,1 + 0,4 + 1,55 - 1,35 = 38,8
ŷ7 = 44,4 - 1,65 + 5,75 - 2,1 + 0,4 - 1,55 + 1,35 = 46,6
ŷ8 = 44,4 + 1,65 + 5,75 - 2,1 - 0,4 + 1,55 + 1,35 = 52,2
Результаты расчетов записываем в 3-й столбец таблицы 1(а)
| № Опыта |  j
| j
| S2j |
| 1 | 40,2 | 41,6 | |
| 2 | 44 | 42,6 | |
| 3 | 52,6 | 51,2 | |
| 4 | 49,2 | 50,6 | |
| 5 | 33 | 31,6 | |
| 6 | 37,4 | 38,8 | |
| 7 | 45,2 | 46,6 | |
| 8 | 53,6 | 52,2 |
Таблица 1(а)
4. Вычислим оценки дисперсий для каждой серии дублированных опытов по формуле: 
= 
где n – число дублированных опытов в каждой серии.
уjL- значение выходной величины в L-м дублированном опыте j-й серии, j=1,2,…, N, L=1,2,…,n.
Для расчетов я буду пользоваться вторым выражением из данной формулы.
S 2 1 =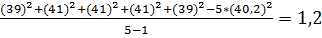 
S 2 2 = 
S 2 3 = 
S 2 4 =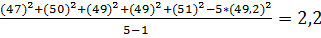 
S 2 5 = 
S 2 6 = 
S 2 7 =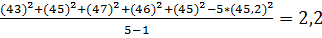 
S 2 8 = 
Запишем полученные результаты расчетов в четвертый столбец таблицы 1(б)
| № Опыта |  j
|  j
| S2j |
| 1 | 40,2 | 41,6 | 1,2 |
| 2 | 44 | 42,6 | 1,5 |
| 3 | 52,6 | 51,2 | 0,3 |
| 4 | 49,2 | 50,6 | 2,2 |
| 5 | 33 | 31,6 | 2,5 |
| 6 | 37,4 | 38,8 | 1,3 |
| 7 | 45,2 | 46,6 | 2,2 |
| 8 | 53,6 | 52,2 | 0,8 |
Таблица 1(б)
5. Проверим однородность дисперсии опытов по критерию Кохрена. Вначале вычисляем расчетное G-отношение по формуле:
G расч = 
, далее по таблицам распределения Кохрена для уровня значимости q=0,05 определяется Gтабл. Если Gрасч< Gтабл, то можно принять гипотезу об однородности дисперсий.
G расч = 
= 0,20
Так как Gрасч = 0,20 < Gтабл = 0,31, то можно принять гипотезу, что дисперсии однородны.
|
|
|
6. Вычислим оценки дисперсии, характеризующей ошибку эксперимента 
. Она вычисляется как среднее арифметическое дисперсий опытов по формуле: 
= 
. Выберу первое выражение:
= 
=18
7. Вычислим дисперсий коэффициентов регрессии. Коэффициенты регрессии bi, bij являются случайными величинами. Дисперсии коэффициентов регрессии характеризуют точность, с которой они найдены. Для ПФП оценки дисперсий всех коэффициентов равны друг другу, определяются по формуле:
= 
8. Оценка значимости коэффициентов регрессии. В результате можно выявить так называемые незначимые коэффициенты регрессии, т.е. те коэффициенты регрессии, которые можно приравнять нулю в математической модели.
Коэффициенты регрессии оказываются незначимыми в том случае, если соответствующий ему фактор или взаимодействие оказывает пренебрежимо малое влияние на изменение выходной величины эксперимента.
Оценка значимости коэффициентов регрессии проводится с помощью t- критерия Стьюдента в следующем порядке:
а) для каждого коэффициента регрессии bi вычисляется расчетное t-отношение по формуле: tрасч i= 
,
tрасч 0 = 
tрасч 1 = 
tрасч 2 = 
tрасч 3 = 
tрасч 12 = 
tрасч 13 = 
tрасч 23 = 
= 2
б) из таблиц t-распределения по величине fу для уровня значимости q=0,05 выбираем табличное t-отношение tтабл = 2,04
в) проверяется условие tрасч≤tтабл. Коэффициенты регрессии, для которых это условие выполняется, являются незначимыми.
Коэффициенты регрессии tрасч 12 и tрасч 23 являются незначимыми, так как tрасч ≤ tтабл.
Коэффициенты регрессии tрасч 0, tрасч 1, tрасч 2, tрасч 3, tрасч 13 являются значимыми, так как tрасч 
tтабл.
9. Проверяем адекватность модели:
а). Вычисляем сумму квадратов, характеризующую адекватность модели Sад. При равномерном дублировании она рассчитывается по формуле: Sад= 
,
Sад = 
б). Вычисляем число степеней свободы fаб, связанное с дисперсией адекватности. При равномерном дублировании и при отсутствии дублированных опытов оно равно:
fад=N-p,
fад = 8 – 7 = 1.
в). Вычислим дисперсию адекватности:
S 
=Sад/fад
S = 15,68 – 1 = 14,68
С помощью F-критерия Фишера для уровня значимости q=0,05 проверяем однородность двух дисперсий: дисперсии адекватности S (с числом степеней свободы fад) и дисперсии, характеризующей ошибку эксперимента (с числом степеней свободы fу).
Fрасч= S / 
Fрасч = 14,68: 18 = 0,81.
Далее по таблицам распределения Фишера определяют величину Fтабл= 2,14. Так как Fрасч ≤ Fтабл, то можно принять гипотезу об однородности дисперсий и найденную математическую модель объекта можно считать адекватной.
10. Анализ результатов эксперимента является заключительным этапом планирования эксперимента, на котором исследователь, пользуясь построенной моделью, получает необходимую информацию об объекте исследования. Анализ модели лучше всего проводить, пользуясь уравнением регрессии в нормализованных обозначениях факторов.
|
|
|
Так как коэффициент регрессии b1 и b2 положительные, то выходная величина возрастает с двух факторов Х1 и Х2.
Так как коэффициент b3 отрицательный, то выходные величины уменьшаются с увеличением фактора Х3.
По уравнению регрессии можно оценить относительную степень влияния варьируемых факторов на изменение выходной величины (относительную значимость факторов). Для этого используем значения t-критерия, вычисленные для каждого линейного коэффициента регрессии.
Так как tрасч 2 получилось наибольшим, то фактор Х2 оказывает наибльшее влияние на выходные величины, по сравнению с факторами Х1 и Х3.
|
|
|
