 |
Подбор сечения колен бруса
|
|
|
|
ЗАДАЧА 2.6. Расчет ломаного бруса на сложное сопротивление
Задание на проектирование:
Для пространственного ломаного консольного бруса требуется:
1. Построить эпюры всех действующих в сечении элемента внутренних сил, принимая значения силы и пары сил равными: Р1=q*a, M1=q*b2.
2. Подобрать размеры стального бруса при допускаемом нормальном напряжении [σ] = 160 МПа. Конструктивно задано:
стержень 1- имеет сплошное круглое сечение;
стержень 2 – имеет сплошное прямоугольное сечение с отношением высоты к ширине как 3:2;
стержень 3 – имеет полое круглое сечение с толщиной стенки, составляющей 20% от наружного диаметра. Подбор сечения производить по эквивалентному моменту
 .
.
3. Проверить прочность элементов бруса, учитывая составляющую нормального напряжения от нормальной силы. При одновременном действии в точке нормальных и касательных напряжений эквивалентные напряжения определяются по теории наибольших касательных напряжений  .
.
Исходные параметры принять равными:
P=40 кН a=2,0 м
M=60 кН.м b=2,5 м
q=20 кН/м c=3,0 м

Рис. 2.6.1. Исходная схема ломаного бруса.
Решение любой задачи по сопротивлению материалов начинаем с освобождения от связей и заменой их реакциями. Система сил, приложенных к брусу, пространственная произвольная. Жесткое защемление в точке D заменяем тремя проекциями реакции и тремя проекциями момента относительно трех координатных осей.
Ранее рассматривалась задача об изгибе консольного бруса в плоскости. Отмечалось, что консольное закрепление освобождает от необходимости искать опорные реакции в обязательном порядке. Аналогично с пространственным брусом. Начинаем решение задачи со свободного конца консоли без определения шести компонент реакции в заделке.
|
|
|
Принимаем систему координат, показанную на рис. 2.6.1. Начало координат на участке AB принимаем в точке A. В произвольном месте рассекаем, задаем координату сечения аппликатой z.
Участок AB 
N(z)=0 нет внешних сил, дающих проекцию на ось Z.
Qx(z)=q.z зависимость линейная. Эпюру строим по двум точкам, значения которых найдем, подставив в функцию поперечной силы значения аппликаты на концах участка:
Qx(z=0)=q.0=0
Qx(z=a)=q.a=20,0.2,0=40,0 кН Строим прямую в координатной плоскости XOZ. Штрихуем параллельно оси ОХ.
Qy(z)=P=40,0 кН Сила постоянная по всей длине участка. Строим прямую параллельную оси отсчета.
Mx(z)=-P.z Изгибающий момент в плоскости YOZ. Эпюра линейная строится по двум значениям, рассчитанным на концах участка:
Mx(z-0)=-P.0=0
Mx(z=a)=-P.a=-40,0.2,0=-80,0 кНм. Эпюру строим со стороны сжатых волокон, т.е. с левой стороны оси бруса.
My(z)=-q.  Изгибающий момент в плоскости XOZ. Зависимость квадратичная. Строим эпюру по трем точкам: две по концам и одна промежуточная. My(z=0)=-q.
Изгибающий момент в плоскости XOZ. Зависимость квадратичная. Строим эпюру по трем точкам: две по концам и одна промежуточная. My(z=0)=-q. 
My(z=a)=-q. 

Mz(z)=0 Отсутствуют внешние силовые факторы, вызывающие крутящий момент в брусе на рассматриваемом участке.

Рис. 2.6.2. Участки бруса ВС и CD с перенесенными силами.
Участок BС 
N(y)=-P=-40,0 кН.
q.a=20,0.2,0=40,0 кН. Поперечная сила в направлении оси ОХ.
Qz(y)=0 В вертикальном направлении поперечная сила равна нулю.
Mx(y)=-P.a=-40,0.2,0=-80 кН.м. Изгибающий момент в вертикальной плоскости постоянный по длине участка.
My(y)= q.  = 20,0.
= 20,0.  =40,0 кН.м. Крутящий момент на участке ВС.
=40,0 кН.м. Крутящий момент на участке ВС.
Mz(y)= -q.a.y Изгибающий момент в горизонтальной плоскости изменяется по линейному закону. Строим эпюру по двум значениям:
Mz(y=0)=0
Mz(y=b)= -q.a.b=-20,0.2,0.2,5=-100 кН.м.
Участок СD 
N(x)=+ q.a =40,0 кН. Участок растянут.
Qy(x)=P=40,0 кН.
Qz(x)=0
Mx(x)=P.a= 40,0.2,0=80 кН.м. Крутящий момент.
My(x)= q.  = 20,0.
= 20,0.  -60=-20 кН.м. Изгибающий момент в вертикальной плоскости.
-60=-20 кН.м. Изгибающий момент в вертикальной плоскости.
Изгибающий момент в горизонтальной плоскости:
Mz(x)= -q.a.b-P.x Линейная функция. Строим по двум точкам.
|
|
|
Mz(x=0)= -q.a.b-P.0=-20,0.2,0.2,5-0=-100 кН.м.
Mz(x=c)= -q.a.b-P.c=-20,0.2,0.2,5-40,0.3,0=-220,0 кН.м.

Рис. 2.6.3. Эпюры силовых факторов в сечениях всех участков ломаного бруса.
Подбор сечения колен бруса
Участок АВ
Опасное сечение в верхней части в месте крепления с горизонтальной балкой ВС. Mx(z=a)=80,0 кНм. изгибающий момент
My(z=a) = 40,0  изгибающий момент
изгибающий момент
Крутящий момент равен нулю
Нормальная сила равна нулю.
Брус находится в деформированном состоянии, называемом СЛОЖНЫМ ИЗГИБОМ.
Поскольку мы не можем допустить, чтобы в сечении напряжения превышали допустимые, которые определены как доля предела текучести материала, то Закон Гука будет выполняться при любых допускаемых нагрузках. Следовательно, при решении применим принцип независимости действия сил или иначе называемый принципом суперпозиции. Принцип суперпозиции допускает раздельное исследование деформации конструкции от каждого внешнего силового фактора с последующим алгебраическим суммированием результатов, если направление напряжений совпадает. В сложных случаях, когда результаты расчета представлены пространственной системой векторов напряжений, для анализа напряженного состояния применяем подходящую теорию прочности.
В нашем случае, при одновременном изгибе относительно двух главных осей сечения, в каждой точке поперечного сечения возникают напряжения, действующие вдоль одного направления. Поэтому применяем алгебраическое суммирование. Для этого определяем точки, в которых напряжения имеют один знак. Для прямоугольного сечения и это делать не обязательно, так как наиболее нагруженными точками будут две угловые, противоположно лежащие точки. В одной напряжения растяжения, а в другой такие же по абсолютной величине, но сжимающие. Записываем условие прочности при сложном пространственном нагружении

Конструктивное соотношение сторон прямоугольника 3:2. Сориентируем брус таким образом, чтобы плоскости действия наибольшего момента и наибольшей жесткости бруса совпадали. Если Mx=80кН.м, а My=40кН.м, то принимаем Wx=b.h2/6, а Wy=b2.h/6. Выражаем h через b, подставляем в условие прочности и решаем относительно b.



Принимаем b=13,26 см и h=20,0 см.
Участок ВС
Опасное сечение в непосредственной близости к узлу С.
|
|
|
Mx(y=b)=80,0 кНм. изгибающий момент
My(y=b) = 40,0  крутящий момент
крутящий момент
Mz(y=b) = 40,0  изгибающий момент
изгибающий момент
N(y=b)=40,0 кН. нормальная сила.
Три силовых фактора вызывают нормальное напряжение, а крутящий момент – касательное напряжение. Пока не известны размеры сечения невозможно определить эквивалентное напряжение и произвести проверку прочности. А чтобы использовать условие прочности для определения размеров, искомый размер, а именно диаметр бруса, входит в геометрические характеристики сечения в разных степенях: в квадрате в площадь сечения и в кубе в осевой и в полярный момент сопротивления. Определение корней кубического уравнения – задача не для “повседневной носки”. Поэтому постараемся обойти эту непростую процедуру методом последовательных приближений. Сначала учитываем только моменты и, решив уравнение относительно куба диаметра, определяем предварительный размер диаметра. Затем находим эквивалентное напряжение уже с учетом всех силовых факторов и сравниваем его с допускаемым. Поскольку включен новый фактор N полученный размер будет недостаточным, чтобы обеспечивать прочность. Во втором приближении даем приращение диаметра и снова проверяем по эквивалентному напряжению. Следующее приращение будет в сторону увеличения или уменьшения размера диаметра в зависимости от нашей “щедрости “ после первой проверки прочности. Глазомер и расчетливость инженера должны способствовать наискорейшему подбору необходимого размера в пределах оговоренной заранее точности решения.
Практический расчет займет меньше места, чем его описание.
Находим эквивалентный момент по теории набольших касательных напряжений:
 .
.
Условие прочности:  , осевой момент сопротивления сплошного круглого сечения:
, осевой момент сопротивления сплошного круглого сечения:  .
.
Подставляем формулу в условие прочности и выражаем из него диаметр:
 .
.
Определяем максимальные касательные и наибольшие нормальные напряжения в опасной точке сечения, а затем эквивалентное напряжение в этой точке и сравниваем его с допускаемым.



|
|
|
С учетом всех силовых факторов эквивалентные напряжения не превышают допускаемые. Расчет закончен, принимаем диаметр бруса равным 205 мм.
Участок СD
Опасное сечение примыкает к заделке в точке В.
Mx(x=c)=80,0 кН. м крутящий момент
My(x=c) =-2 0,0  изгибающий момент
изгибающий момент
Mz(x=c) =-22 0,0  изгибающий момент
изгибающий момент
N(x=c)=40,0 кН. нормальная сила.
Алгоритм расчета на третьем участке повторяет решение на предыдущем.
 .
.
 .
.
Принимаем предварительно диаметр 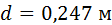 .
.
 ,
,


Принимаем диаметр бруса равным 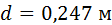 .
.
Расчет закончен.
|
|
|


