 |
Оценка качества подобранных моделей.
|
|
|
|
Лабораторная работа
Построение кривых роста (функций времени)
(Microsoft Excel)
Необходимо построить семейство кривых роста и выбрать наилучшую.
Откройте файл Кривые роста.xls, который содержит данные численности занятых на крупных предприятиях Республики Марий Эл с января 2000 года по декабрь 2005 года включительно.
Построение кривых роста.
Для отображения основной тенденции развития явления во времени или модели этого процесса применяются различные уравнения: полиномы разной степени, экспоненты, логистические кривые и другие функции времени или кривые роста.
Определим линейный тренд для исходного динамического ряда.
· Для удобства расчетов, скопируйте данные первого листа на Лист 2;
· Переименуйте лист 2 на «Виды трендов»;
· По исходным данным столбца В и столбца С создайте точечную диаграмму:
- Выделите мышью столбцы В и С;
- Перейдите на вкладку «Вставка»;
- Выберите тип диаграммы «Точечная»: «Точечная с маркерами»;
- Перейдите на вкладку «Макет»;
- Задайте названия осей диаграммы: ось X – Даты, ось Y – Численность занятых, тыс. чел.
· В полученной диаграмме измените формат оси Y:
- При помощи щелчка правой кнопкой мыши на оси Y вызовите контекстное меню;
- Выберите пункт Формат оси;
- На вкладке «Параметры оси» установите Минимальное значение 190;
- Максимальное значение установите 250;
- Цена основных делений – 10
- Нажмите кнопку «Закрыть».
· В полученной диаграмме измените формат оси X:
- При помощи щелчка правой кнопкой мыши на оси X вызовите контекстное меню;
- Выберите пункт Формат оси;
- На вкладке «Параметры оси» установите Минимальное значение 36526 (соответствует числу 01.01.2000 в формате Дата);
|
|
|
- Максимальное значение установите 38687 (соответствует числу 01.12.2005 в формате Дата);
- Цена основных делений – 120 (соответствует длине периода в один квартал);
- Перейдите на вкладку «Выравнивание»;
- В поле «Направление текста» задайте вариант «Повернуть весь текст на 270 градусов»;
- Нажмите кнопку «Закрыть».
· Разместите легенду внизу диаграммы:
- Перейдите на вкладку «Макет» и выберите пункт «Легенда»: «Добавить легенду снизу».
· Увеличьте размер диаграммы.
После произведенных преобразований точечная диаграмма «Динамика численности занятых на крупных предприятиях в РМЭ» примет следующий вид:

· Добавим линию тренда для исследуемого динамического ряда:
- При помощи щелчка правой кнопкой мыши на ряде данных вызовите контекстное меню;
- Выберите пункт «Добавить линию тренда»;
- На вкладке «Параметры линии тренда» определите функцию аппроксимации – Линейная;
- Задайте флажки в полях «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)»;
- Нажмите кнопку «Закрыть».
Получим следующую диаграмму:

Подбор выравнивающей кривой с использованием линейной аппроксимирующей функции позволил определить уравнение линейного тренда для исходного динамического ряда:

По аналогии с определением линейного тренда на отдельных листах определите уравнения трендов на основании логарифмического, полиномиального, экспоненциального, степенного выравниваний.
Для логарифмического выравнивания исходного ряда имеем:

Подбор выравнивающей кривой с использованием логарифмической аппроксимирующей функции позволил определить уравнение логарифмического тренда для исходного динамического ряда:

На основании выравнивания с использованием полинома второго порядка:
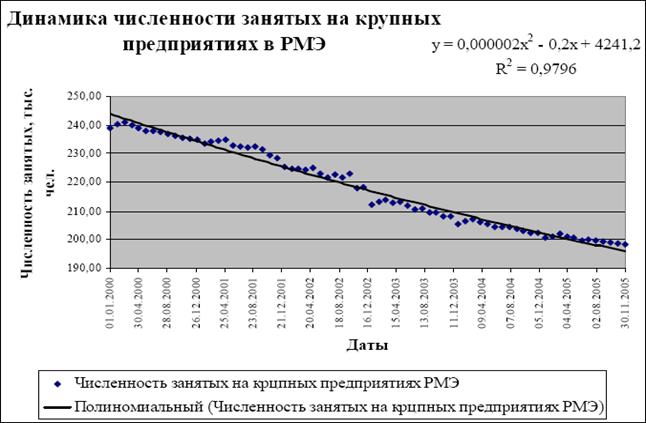
Подбор выравнивающей кривой с использованием аппроксимирующего полинома второго порядка позволил определить уравнение тренда для исходного динамического ряда:
|
|
|

На основании выравнивания с использованием степенного тренда имеем:

Подбор выравнивающей кривой с использованием степенного тренда позволил определить уравнение тренда для исходного динамического ряда:

На основании выравнивания с использованием экспоненциального тренда имеем:

Подбор выравнивающей кривой с использованием экспоненциального тренда позволил определить уравнение тренда для исходного динамического ряда:

Оценка качества подобранных моделей.
Одним из способов сравнения качества подобранных моделей является метод сравнения коэффициентов детерминации:
Для анализа качества моделей на Листе 3 (Переименуйте его на - «Коэффициенты детерминации») создайте таблицу:

Заполните таблицу, сделайте вывод о лучшем способе аппроксимации исходного временного ряда
Так как исходный ряд, характеризующий численность занятых на крупных предприятиях в республике Марий Эл, содержит равностоящие друг от друга уровни (т.е. все наблюдения брались через месяц), тогда для подбора наиболее подходящей формы кривой может служить метод конечных разностей.
· Расчеты производите на Листе 4, для этого перейдите на Лист 4;
· Переименуйте его на «Оценка качества»;
· Скопируйте данные первого листа на лист «Оценка качества»;


· Создадим шапку расчетной таблицы, для этого
в ячейку D1 поместим запись «Разностный оператор первого порядка»,
в ячейку E1 поместим запись «Разностный оператор второго порядка»,
в ячейку F1 поместим запись «Разностный оператор третьего порядка»,
в ячейку G1 поместим запись «Разностный оператор четвертого порядка»,
в ячейку H1 поместим запись «Темпы роста».
· Рассчитаем разностные операторы первого порядка:
- Установите курсор мыши в ячейке D2;
- Для нахождения разностного оператора первого порядка для значения второго уровня ряда (для первого найти невозможно, т.к. нет предыдущего значения) в ячейку D2 введите формулу соответствующую оператору  «=D3-D2».
«=D3-D2».
- Для нахождения разностного оператора первого порядка для оставшихся значений уровней по аналогии наведите курсор мыши на нижний правый угол ячейки D2;
|
|
|
- при появлении «черного крестика», не отпуская левую кнопку мыши, «растяните» формулу на все уровни ряда.
· Рассчитаем разностные операторы второго порядка: E4-E3. Для этого:
- Установите курсор мыши в ячейке E4;
- Для нахождения разностного оператора второго порядка для значения третьего уровня ряда (для первого и второго найти невозможно) в ячейку E4 введите формулу соответствующую  «=E4-E3».
«=E4-E3».
- Рассчитайте разностные операторы второго порядка для всех оставшихся уровней ряда.
· Самостоятельно найдите значения разностных операторов третьего и четвертого порядков;
· Рассчитаем темпы роста уровней ряда:
- Так как темп роста рассчитывается по формуле

то соответственно в ячейку H2 введем формулу: «=C3/C2*100»;
· Найдите темпы роста для всех оставшихся уровней ряда.
Существуют следующие критерии выбора класса выравнивающих прямых:

Для выбора подходящего критерия отбора выравнивающей кривой рассчитаем средние квадратические отклонения для построенных рядов с использованием статистической функции КВАДРОТКЛ.
Статистическая функция КВАДРОТКЛ определяет сумму квадратов отклонений для анализируемого диапазона данных.
Самостоятельно рассчитайте квадратические отклонения по всем разностным операторам. Лучшим считается уравнение тренда с наименьшей суммой квадратов отклонений.
Сделайте вывод о наилучшей форме тренда, используя вышеуказанную таблицу.
Произведите подобные вычисления для данных своего варианта и создайте отчет в MS Word.
|
|
|


