 |
Теория метода капиллярного вискозиметра
|
|
|
|
Лабораторная работа № 7
Определение коэффициента вязкости газов и средней длины пробега
Молекул
Цель работы:
1. Ознакомиться с явлением вязкости и теоретическими представлениями о механизме возникновения сил вязкого трения.
2. Изучить особенности протекания жидкостей и газов по трубам.
3. Освоить метод капиллярного вискозиметра для измерения вязкости газа.
Приборы и принадлежности:
1. Капилляр.
2. Манометр.
3. Аспиратор.
4. Секундомер.
5. Миллиметровая линейка.
5. Мензурка.
Краткая теория
Явления вязкости, теплопроводности, диффузии относятся к явлениям переноса. Они возникают в термодинамических системах при отклонении их от равновесного состояния. Так, если создать разность температур в различных областях объёма газа, то возникнет поток тепла, стремящийся восстановить равновесие. Это явление переноса тепла в неравновесной термодинамической системе называется теплопроводностью.
Если внешние силы вызывают перемещение одного слоя жидкости относительно другого, то внутри жидкости между слоями возникают силы стремящиеся затормозить это движение. Это явление называют внутренним трением, или вязкостью. Механизм его возникновения связан с тем, что вследствие теплового движения молекулы переходят из одного слоя в другой, перенося с собой импульс направленного движения. В результате возникает перенос импульса из тех слоев, где скорость потока больше в те слои, где скорость движения меньше и наоборот.
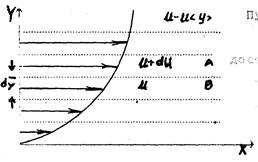
Рис. 1 Распределение скоростей в слоях потока газа.
Пусть вдоль оси Х движется поток газа. Разобьём поток на параллельные, достаточно тонкие слои dy так, чтобы скорости направленного движения молекул U внутри каждого слоя были приблизительно одинаковы (рис. 1). Как видно из рисунка скорости U в слоях одинаковы по направлению, но различны по величине, так что скорость слоя есть функция координаты y: U=U(y).
|
|
|
Быстрота изменения скорости вдоль оси у характеризуется производной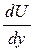 
, которая называется градиентом скорости по направлению у. Так как имеет место перенос импульса из одного слоя (В) в другой (А), то согласно законам механики изменение импульса слоя А со временем равно силе, действующей со стороны слоя В. Пусть S – площадь соприкосновения слоев, тогда согласно эмпирическому закону Ньютона для сил внутреннего трения имеем:
F= - η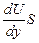 
(1), где сила F направлена по касательной к границе разделов слоев, η – коэффициент вязкости (внутреннего трения). Размерность η в системе СИ - Па·с.
Теория метода капиллярного вискозиметра
Рассмотрим движение газа (или вязкой жидкости) по трубе круглого сечения в направлении оси Х. При малых скоростях потока движение оказывается ламинарным (слоистым). Скорости направленного движения частиц газа медленно изменяются вдоль оси у и параллельны оси Х. При втекании газа в трубу, скорости слоев вначале постоянны по всему сечению (Х =0), а с увеличением координаты Х распределение скоростей меняется и на некотором расстоянии Х 0 носит характер параболического распределения (рис.2). В дальнейшем, при установившемся ламинарном потоке, оно уже не меняется.
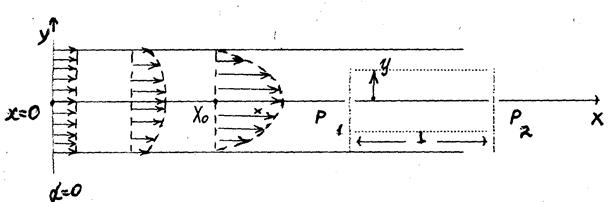
Рис.2.
Выделим в жидкости малый цилиндр радиуса у и длины l. Обозначим давления на его торцах Р1 и Р2. При Х ≥Х0 (установившееся течение) сила давления на цилиндр (Р1-Р2)πу2 уравновешивается силой внутреннего трения, действующей на поверхность цилиндра со стороны окружающих его слоёв жидкости. Согласно формуле (1) эта сила равна: F= - η2 πуl 
(2).
Условие стационарности потока тогда запишется так:
η2πуl +(Р1-Р2)πу2=0 (3), откуда dU равно: dU=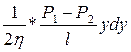 
(4). Интегрируя это равенство по у, найдём V=- 
(5), где C – постоянная интегрирования, которую найдём из граничного условия. При y=R скорость газа обращается в нуль, т.е. молекулы газа как бы прилипают к стенке (движение молекул газа здесь тормозится до нуля, из-за взаимодействия их с молекулами стенки).
|
|
|
Тогда: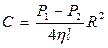 
(6). Для зависимости скорости слоя газа от его координаты получим: 
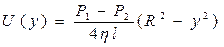(7), т.е. действительно, скорость максимальна на оси трубы и квадратично убывает до нуля с приближением к стенке (рис.2). Объём газа, протекающий через трубу за время t равен:
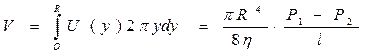(8).
Равенство (8) называется формулой Пуазейля-Хагена. Используя её, можно экспериментально определить вязкость газа, если известен объём газа V, прошедший через трубку длиной l за время t, ее радиус R и перепад давления на торцах трубы: 
(9).
|
|
|
