Лекция 7. Гармонические функции и их свойства

Рассмотрим уравнение Лапласа на плоскости

(33)

и в пространстве

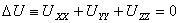
(34)

 

Уравнение (33) при переходе к полярным координатам преобразуется к виду

 

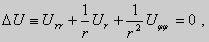
(33*)

 

Рис 14 Рис 14.1

Если в пространстве перейти к сферическим координатам

 

то уравнение (34) примет вид

 

 

(34*)

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных - круговой) симметрией.

Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим

где C₁ и C₂ - произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию

 

которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U₀ является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

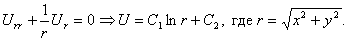
Выбирая С₁=-1 и С₂=0, будем иметь функцию

которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция U₀ удовлетворяет уравнению Лапласа (33) всюду на плоскости, кроме начала координат 0, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q, помещенным в начало координат. Тогда потенциал этого поля равен

 

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен

где q₁ - линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.

 

Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

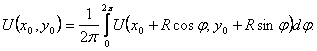
(35)

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)

 

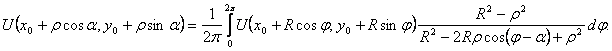
Если в этой формуле положить ρ=0, то получится формула (35).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где (см. рис.15.1):

 

Рис. 15 Рис. 15.1

 

(36)

Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

или

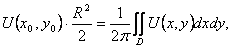
где D - круг радиуса R. Разделив обе части полученного равенства на R²/2, будем иметь

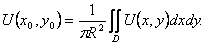
(37)

В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D. Из формулы (37) получается:

Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

(38)

Число 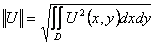называют нормой функции U=U(x,y) в области D, и неравенство (38) можно переписать в виде

 

Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

 

Применим это неравенство к формуле (37):

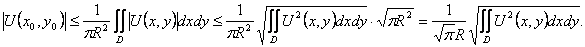
Что и требовалось доказать.

Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

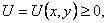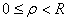Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o, у_o) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству

 

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство. Если функция U=U(x, у) ограничена сверху, то U₁=-U(x, y) - ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака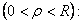

 

Если функция U(x, у) гармоническая во всей плоскости 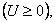то, фиксировав произвольное 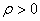и неограниченно увеличивая R мы получим

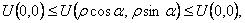
то есть Теорема Лиувилля доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.

 

Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(x_o, у_o, z_o) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

 

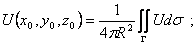
б) ее среднему значению в шаре D, то есть

 

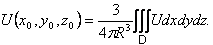
Поделиться:

Воспользуйтесь поиском по сайту: