 |
ЗАДАЧА 2.8. Подбор сечения стойки под заданную нагрузку
|
|
|
|
Задание на проектирование:
Стальная стойка, защемленная одним концом и шарнирно опертая на другом, сжимается осевой силой Р. Из условия устойчивости определить размеры поперечного сечения стойки, форма которого задана. В расчетах принять [σ] = 160 МПа. Е=2. 105 МПа.
Уголки, из которых набрана стойки, разнесены и образуют квадрат со стороной a=200 мм. Высота стойки равна L=6000мм, сжимающая сила равна P=80кН.
Подобранное сечение должно обеспечивать прочность опорной конструкции и её устойчивость, то есть способность сохранять прямолинейную форму оси опоры при действии осевой сжимающей силы. Мы не будем рассматривать конструктивные решения, обеспечивающие неизменный наружный размер опоры.
В отличие от сжатия короткой колонны задача устойчивости не решается в одно действие. Для решения воспользуемся методом расчета, в котором вводится коэффициент снижения допускаемого напряжения φ при продольном изгибе.
Идея метода состоит в том, что площадь сечения стержня, подобранная из условия прочности, не обеспечивает сохранение прямолинейной формы оси при продольном сжатии. Возьмем в руки стальную слесарную линейку шириной 20 мм и толщиной 0.5 мм. В первом приближении можно считать безопасной нагрузкой для него растягивающую силу в 200 кг. Попробуем изменить направление силы и сжать линейку кончиками указательных пальцев двух рук. Не ощутив существенного сопротивления, увидим, как линейка искривляется в руках. Это явление и называется потерей устойчивости при осевом сжатии. Если свернуть линейку в продольную трубочку или в гармошку и повторить испытания, то растягивающая сила не изменится, а сжимающая существенно возрастёт, и скорее всего нам не удастся добиться искривления линейки с новой формой поперечного сечения, только сжимая её пальцами. Этот опыт должен навести нас на мысль, что при деформации сжатия удлиненных стержней площадь сечения не является определяющей геометрической характеристикой при подборе сечения в отличие от осевого растяжения. В формулу условия прочности при осевом сжатии вводится поправочный коэффициент, увеличивающий расчетную площадь. Этот коэффициент снижения допускаемого напряжения задается в виде графика или в табличной форме, как функция гибкости стержня.
|
|
|
Гибкостью называют параметр, который связывает длину стержня, минимальный осевой момент инерции поперечного сечения, площадь сечения и условия закрепления стержня зависимостью:
,
где L - длина стержня в [м];
𝜇- коэффициент приведения длины, показывающий какую часть длины искривленного стержня занимает одна полуволна синусоиды;
-минимальный радиус инерции сечения в [м];
– минимальный из двух главных моментов инерции поперечного сечения стержня в [м4];
F - площадь поперечного сечения в [м2].
Рис. 2.8.1. Форма стержня, потерявшего устойчивость.
В начальный момент расчета мы не имеем представления о размерах сечения, поэтому зададимся произвольным значением коэффициента снижения допускаемого напряжения 𝝋0=0,5. Рассчитаем предварительную величину площади сечения одного уголка:
По ГОСТ на уголок равнобокий выбираем ближайший подходящий профиль. Это уголок 40*40*4 уголок с шириной полки 40 мм и толщиной полки 4 мм. Выписываем параметры профиля необходимые для продолжения расчета: F=3,08см2, Jx=4,58см4, z0=1,13см.
|
| Рис. 2.8.2. Форма поперечного сечения стержня. |
Сечение из четырех одинаковых равнобоких уголков имеет две оси симметрии, поэтому центр тяжести определится без расчетов на пересечении осей симметрии. Главные моменты инерции сечения одинаковые, и определяются по формуле:
|
|
|
Общая площадь сечения FΣ=4.F=4.3,08=12,32 см2.
Коэффициент приведения длины для случая защемления на одном конце и шарнирного опирания на втором равен 𝜇=0,7.
Радиус инерции сечения 
Гибкость стержня 
безразмерная величина.
В таблице коэффициентов снижения допускаемых напряжений значения гибкости изменяются с шагом 10 единиц. Выписываем два значения коэффициента 𝝋 для 𝜆 равного 40 и 50.
Для 𝜆=40 𝝋=0,92
𝜆=50 𝝋=0,89. Значение 𝝋 для 𝜆=47 рассчитываем путем линейной интерполяции
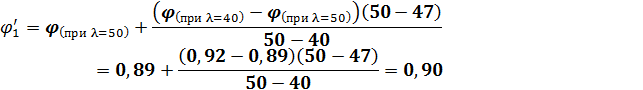
Для ускорения сходимости решения определяем значение коэффициента, подставляемого в формулу, как среднее арифметическое между 𝝋 предыдущего приближения и новым значением, снятым из таблицы.
Определим площадь сечения уголка во втором приближении
Подбираем по ГОСТ уголок 25*25*4 уголок с шириной полки 25 мм и толщиной полки 4 мм. Выписываем параметры профиля необходимые для продолжения расчета: F=1,86см2, Jx=1,03см4, z0=0,76см.
Подбираем по ГОСТу уголок 28*28*3. Выписываем параметры профиля: F=1,62см2, Jx=1,16см4, z0=0,80см.
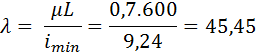
Принимаем уголок 28*28*3.
Решение завершено.
|
|
|
