ЗАДАЧА 2.9. Подбор сечения бруса, воспринимающего усилие от падающего груза

Задание на проектирование:

На упругую систему с высоты h падает груз Р. Подобрать размеры бруса круглого поперечного сечения из малоуглеродистой стали. В расчетах принять [σ] = 160 МПа. Е=2. 10⁵ МПа. Массу упругой системы не учитывать.

Р=200 Н   a=1,5м   h=0,05 м

 

Рис. 2.9.1. Исходная расчетная схема задачи.

Ломаная балка опирается на шарнирно неподвижные опоры. Таким образом, на конструкцию наложены четыре внешние связи, что делает балку один раз статически неопределимой.

Раскрываем статическую неопределимость. Для этого освобождаемся от одной связи, а именно допускаем горизонтальное смещение правой опоры. Действие отброшенной связи заменяем неизвестной реакцией связи Х₁ и получаем эквивалентную систему конструкции (рис. 2.9.2). Считаем силу Р статически приложенной.

При выборе основной системы нужно внимательно анализировать предоставляемую свободу конструкции, чтобы последняя не превратилась в мгновенный механизм, в котором какие-то узлы или точки получают значительные перемещения.

Составляем каноническое уравнение метода сил. Это уравнение описывает горизонтальное смещение правого конца ломаного бруса от всех действующих на систему сил, и его мы приравниваем нулю, поскольку реальная неподвижная опора не допускает подобное перемещение.

 

, (2.9.1)

где 𝜹₁₁ – перемещение в направлении силы Х₁ от единичного силового вектора, приложенного и направленного как сила Х₁;

𝜟_Р1 – перемещение в направлении силы Х₁ от действия всех внешних сил, приложенных к основной системе.

Рис.2.9.2. Эквивалентная система задачи.

Прикладываем единичную силу Х₁, т.е. вместо неизвестной силы прикладываем единичный силовой вектор.

Рис.2.9.3. Эпюра изгибающего момента от единичной силы.

Строим эпюру изгибающих моментов, действующих в сечениях стойки и ригеля. Построение можно вести классическим путем или упрощенным. Рассмотрим упрощенный способ.

Приложенная единичная сила вызывает появление опорных реакций в шарнирных опорах. В левом неподвижном шарнире реакция разложится на две составляющие: горизонтальную и вертикальную. Горизонтальная должна равняться единице, поскольку она противодействует силе Х₁=1. И другой она тоже не может быть, потому что других сил, которые бы удерживали её нет. Момент на стойке описывается линейной функцией, с нулевым значением в шарнире и Mz(y=a)=1*a в верхнем сечении стойки рис. 2.9.3. Стойка и ригель жестко соединены в углу, поэтому в крайнем левом сечении ригеля момент имеет ровно такое же значение. Образно говоря, переносим циркулем момент со стойки на ригель. На правом конце ригеля опять шарнир, следовательно, момент в сечении над шарниром равен нулю. Других сил в пролете ригеля нет, потому эпюра линейно изменяется от 1*а до нуля.

Рис.2.9.4. Эпюра изгибающего момента от внешней нагрузки.

Эпюра изгибающего момента от внешней нагрузки представлена на рисунке 2.9.4. Горизонтальная составляющая реакции в левой опоре равна нулю, поэтому стойка свободна от внутреннего момента. Ригель нагружен силой посередине пролета, поэтому эпюра будет такая же, как для однопролетной шарнирно-опертой балки: равнобедренный треугольник с вершиной

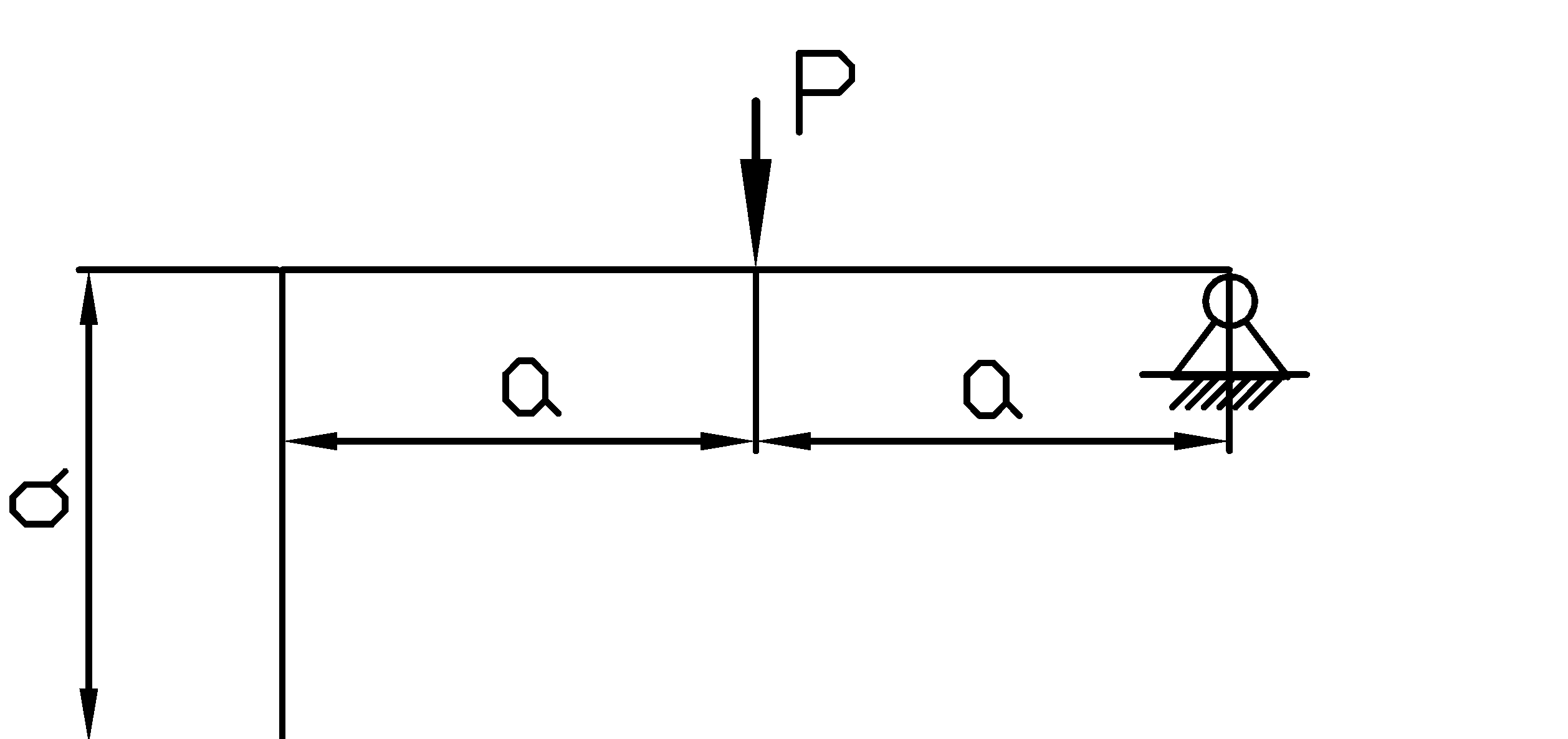
Вычисляем коэффициенты уравнения перемещений (2.9.1) способом Верещагина. Умножаем единичную эпюру саму на себя для нахождения 𝜹₁₁

.

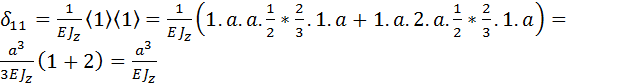Для определения свободного члена уравнения 𝜟_Р1 перемножаем эпюру от внешней нагрузки, которую называют ‘грузовая’, и единичную

.

.

Любым способом строим суммарную эпюру изгибающих моментов ломаного бруса рис. 2.9.5.

Рис. 2.9.5. Результирующая эпюра изгибающих моментов ломаной балки	Рис. 2.9.6. Эпюры для определения статического прогиба в точке падения груза

Опасное сечение бруса определяем по результирующей эпюре. Наибольший изгибающий момент действует в месте падения груза. Наибольшие напряжения, которые возникают в опасном сечении при ударе, определим, умножив максимальные напряжения при статическом приложении нагрузки на коэффициент динамичности

–условие прочности при ударе.

(2.9.2)

где - - высота падения груза [м];

прогиб в точке падения груза при статическом приложении этой же нагрузки.

Статический прогиб в месте падения груза определим способом Верещагина. К основной системе в точке падения груза прикладываем единичную силу, строим эпюру изгибающих моментов (рис. 2.9.6). Умножаем результирующую статическую эпюру (рис. 2.9.5) на единичную (рис. 2.9.6):

 

= .

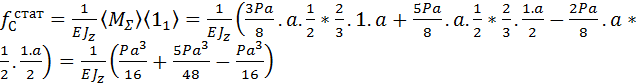Осевой момент инерции сплошного круглого сечения .

Осевой момент сопротивления этого сечения .

Максимальные нормальные напряжения при статической нагрузке определим по формуле

. (2.9.3)

 

Коэффициент динамичности определится после подстановки выражения статического прогиба

. (2.9.4)

 

(2.9.5)

Решение неравенства (2.9.5) относительно диаметра представляется затруднительным, поэтому упростим выражение коэффициента динамичности, удалив единицы из-под радикала и из скобок. Запишем условие прочности в упрощенном виде:

(2.9.6)

 

Решаем относительно d:

Определяем динамические напряжения в брусе при расчетном диаметре

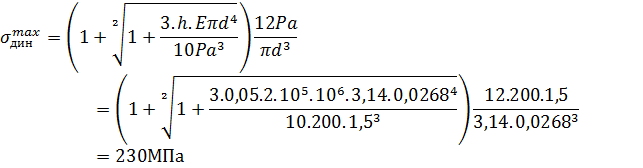
Получили напряжение на 43,75% превышающее допускаемые. Далее подбираем диаметр d₁ методом последовательных приближений. Упуская зависимость в скобках, примем, что напряжения обратно пропорциональны кубу диаметра. Запишем d₁³=1,438 d³. d₁=0,0302м.

 

Превышение напряжения на 18%. Принимаем следующее значение диаметра: d₂=0,0302. 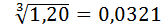м

 

Превышение напряжения на 7,8%. Принимаем следующее значение диаметра: d₃=0,0321. м

 

На этом шаге можно прервать приближения и принять диаметр бруса равным: d=33мм.

Следует сказать, что можно было ограничиться предварительным значением диаметра d=27мм. Дело в том, что при ударном приложении нагрузки, прочностные характеристики возрастают до 100%. Таким образом, мгновенное возрастание напряжений компенсируется повышением допускаемого напряжения до 320 МПа, что несколько больше 230МПа, которые были получены выше.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: