 |
Проведение эксперимента и обработка результатов
|
|
|
|
Лабораторная работа № 9
Определение отношения молярных теплоёмкостей для воздуха γ
Методом Клемана-Дезорма
Цель работы:
1. Изучение метода использования 1-го начала термодинамики к исследованию различных термодинамических процессов в идеальных газах.
2. Экспериментальное определение отношения молярных теплоёмкостей для воздуха.
3. Освоение метода теоретического расчёта теплоёмкостей газов при различных процессах.
Оборудование:
1. Стеклянный сосуд с двумя кранами.
2. U - образный водяной манометр.
3. Ручной насос Шинца.
4. Секундомер.
Краткая теория
Термодинамика изучает системы, состоящие из огромного числа частиц, находящихся в непрерывном хаотическом движении. Методы описания поведения таких сложных систем принципиально отличаются от принятых в механике. При термодинамическом подходе к изучению таких систем не рассматривают поведение каждой частицы в отдельности и те внутренние механизмы, которые приводят к протеканию тех или иных процессов в системе. Термодинамика использует понятия и физические величины, относящиеся ко всей системе в целом, такие как внутренняя энергия, давление, объём, температура и т. д.
Все теоретические построения термодинамики исходят из весьма общих эмпирических законов, которые называются началами термодинамики. Первое начало представляет собой закон сохранения и превращения энергии в применении к термодинамическим системам. Второе начало указывает направление развития процессов, протекающих в системе. Третье начало накладывает ограничения на процессы, которые приводили бы к достижению абсолютного нуля температур.
Запишем уравнение и формулировку Первого начала Термодинамики:  (1). Элементарное количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение системой элементарной работы. Рассмотрим смысл величин, входящих в уравнение (1).
(1). Элементарное количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение системой элементарной работы. Рассмотрим смысл величин, входящих в уравнение (1). 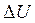 - изменение внутренней энергии системы. С точки зрения статистической физики внутренняя энергия системы состоит из кинетической энергии поступательного и вращательного движения молекул, колебательного движения атомов, потенциальной энергии взаимодействия молекул и атомов в молекулах. Для идеального газа, где взаимодействие частиц считается пренебрежительно малым, потенциальная энергия взаимодействия принимается равной нулю и формула для расчета внутренней энергии выглядит следующим образом:
- изменение внутренней энергии системы. С точки зрения статистической физики внутренняя энергия системы состоит из кинетической энергии поступательного и вращательного движения молекул, колебательного движения атомов, потенциальной энергии взаимодействия молекул и атомов в молекулах. Для идеального газа, где взаимодействие частиц считается пренебрежительно малым, потенциальная энергия взаимодействия принимается равной нулю и формула для расчета внутренней энергии выглядит следующим образом: 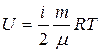 (2), здесь i – число степеней свободы молекулы. Таким образом, внутренняя энергия идеального газа зависит только от температуры и, следовательно, может быть однозначно выражена через макроскопические параметры состояния системы: P, V, T. Поэтому говорят, что U есть функция состояния системы. Изменение внутренней энергии в ходе элементарного процесса, найдём дифференцированием уравнения (2):
(2), здесь i – число степеней свободы молекулы. Таким образом, внутренняя энергия идеального газа зависит только от температуры и, следовательно, может быть однозначно выражена через макроскопические параметры состояния системы: P, V, T. Поэтому говорят, что U есть функция состояния системы. Изменение внутренней энергии в ходе элементарного процесса, найдём дифференцированием уравнения (2): 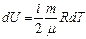 (3). В ходе конечного процесса 1-2 (рис.1) изменение внутренней энергии можно найти интегрированием уравнения (3):
(3). В ходе конечного процесса 1-2 (рис.1) изменение внутренней энергии можно найти интегрированием уравнения (3):  (4).
(4).
|
|
|
Из (4) видно, что 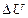 не зависит от пути перехода системы из состояния 1 в состояние 2, т.к. однозначно определяется через параметры P, V, T конечного и начального состояний.
не зависит от пути перехода системы из состояния 1 в состояние 2, т.к. однозначно определяется через параметры P, V, T конечного и начального состояний.
Второе слагаемое уравнения (1) δА – элементарная работа, совершённая в ходе бесконечно малого изменения параметров системы. Известная формула из механики для работы может быть преобразована к следующему виду: δА=PdV (5). В ходе конечного процесса 1-2 работа равна: 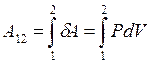 (6).
(6).
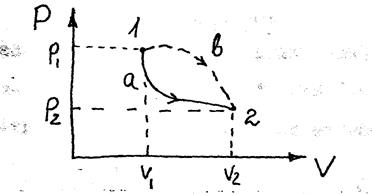
Рис. 1
Из этих формул видно, что если система сама совершает работу (dV > 0), то работа положительна и считается отрицательной, если над системой совершается работа (dV < 0). Исходя из геометрического смысла интеграла (см. (6) и рис. 1) легко видеть, что работа зависит от типа процесса при переходе из 1-2 (т. е. от пути перехода на рис. 1), например, Ав > Аа. поэтому говорят, что работа является функцией процесса. Для того, чтобы рассчитать интеграл в (6), надо знать, по какому закону изменяются параметры Р, V, Т при переходе 1 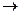 2.
2.
|
|
|
Левая часть уравнения (1) 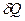 - элементарное количество теплоты. Как и работа, эта величина является мерой изменения энергии системы в ходе процесса. Различие Q и А в том, что если работа оценивает изменение любого вида энергии (механической, электрической, магнитной), то количество теплоты без предварительного преобразования в работу (например, в ходе процесса, когда не изменяются внешние параметры системы: при теплообмене нагретого и холодного тела) оценивают только изменение внутренней энергии. Как и в случае работы, количество теплоты, которое потребуется на совершение процесса 1-2 зависит от того, по какому пути будет развиваться процесс (а или в, на рис.1), так что Q также является функцией процесса: δ Q> 0, если тепло поступает в систему и δ Q< 0, если тепло выходит из системы. Исходя из вышесказанного ясно, что бессмысленно говорить о величине работы или количестве теплоты в состоянии 1 или 2 без указания пути перехода.
- элементарное количество теплоты. Как и работа, эта величина является мерой изменения энергии системы в ходе процесса. Различие Q и А в том, что если работа оценивает изменение любого вида энергии (механической, электрической, магнитной), то количество теплоты без предварительного преобразования в работу (например, в ходе процесса, когда не изменяются внешние параметры системы: при теплообмене нагретого и холодного тела) оценивают только изменение внутренней энергии. Как и в случае работы, количество теплоты, которое потребуется на совершение процесса 1-2 зависит от того, по какому пути будет развиваться процесс (а или в, на рис.1), так что Q также является функцией процесса: δ Q> 0, если тепло поступает в систему и δ Q< 0, если тепло выходит из системы. Исходя из вышесказанного ясно, что бессмысленно говорить о величине работы или количестве теплоты в состоянии 1 или 2 без указания пути перехода.
Под теплоёмкостью всей системы понимают отношение: 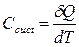 (7), она численно равна количеству тепла, необходимого для изменения температуры на один градус. На практике более часто используются понятия удельной
(7), она численно равна количеству тепла, необходимого для изменения температуры на один градус. На практике более часто используются понятия удельной 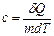 (8) и молярной теплоемкости:
(8) и молярной теплоемкости: 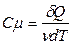 (9). Поскольку δ Q - функция процесса, то и Ссист, с, Сµ являются функциями процесса, зависят от того, при каких условиях осуществляется процесс. Воспользуемся первым началом (1) для анализа некоторых простых процессов и рассчитаем молярные теплоёмкости для них (при m = const).
(9). Поскольку δ Q - функция процесса, то и Ссист, с, Сµ являются функциями процесса, зависят от того, при каких условиях осуществляется процесс. Воспользуемся первым началом (1) для анализа некоторых простых процессов и рассчитаем молярные теплоёмкости для них (при m = const).
1. Изохорический процесс (V=const). Уравнение процесса следует из уравнения Менделеева-Клапейрона: 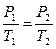 (10). Используя (1) и (5), запишем 1 начало в виде: δQ=dU+pdV. Поскольку V=const, то δА=0 и δQ=dU, в ходе этого процесса подводимое к системе количество теплоты идёт только на увеличение внутренней энергии системы. С учётом (3)
(10). Используя (1) и (5), запишем 1 начало в виде: δQ=dU+pdV. Поскольку V=const, то δА=0 и δQ=dU, в ходе этого процесса подводимое к системе количество теплоты идёт только на увеличение внутренней энергии системы. С учётом (3)  (11). За счёт подводимого тепла повышается температура системы (δQ> 0, следовательно, dT> 0). Молярную теплоёмкость для этого процесса обозначим СV:
(11). За счёт подводимого тепла повышается температура системы (δQ> 0, следовательно, dT> 0). Молярную теплоёмкость для этого процесса обозначим СV: 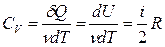 (12). Внутренняя энергия (2) может быть выражена через СV:
(12). Внутренняя энергия (2) может быть выражена через СV: 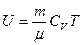 (13).
(13).
|
|
|
2. Изотермический процесс (T=const). Уравнение процесса: PV=const или P1V1=P2V2 (14). Поскольку dT=0, то dU=0 и первое начало для этого процесса: δQ=dА=pdV, всё подводимое тепло идёт на совершение работы, без изменения внутренней энергии. Работу в ходе данного процесса вычислим, выражая давление через параметры V и T из уравнения Менделеева-Клапейрона: 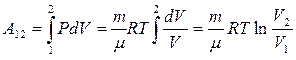 (15). Теплоёмкость этого процесса
(15). Теплоёмкость этого процесса 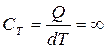 .
.
3. Изобарический процесс(Р=const). Уравнение процесса: 
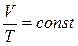 или
или 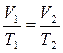 (16). Тогда 1 начало для этого процесса:
(16). Тогда 1 начало для этого процесса: 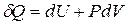 (1`), в ходе этого процесса за счёт подводимого тепла изменяется внутренняя энергия и совершается работа (которая идёт на изменение объёма системы). Работа в ходе этого процесса: A12=
(1`), в ходе этого процесса за счёт подводимого тепла изменяется внутренняя энергия и совершается работа (которая идёт на изменение объёма системы). Работа в ходе этого процесса: A12= 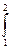 PdV=P(V2-V1). Теплоемкость Cp для изобарического процесса с учётом (1`) и (13): Cp =
PdV=P(V2-V1). Теплоемкость Cp для изобарического процесса с учётом (1`) и (13): Cp = 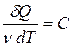 v+
v+ 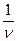 P
P 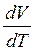 (17). Дифференцируя уравнение Менделеева-Клапейрона (при P=const) PdV=νRdT (откуда
(17). Дифференцируя уравнение Менделеева-Клапейрона (при P=const) PdV=νRdT (откуда 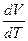 = νR/P подставим в (17)), найдём связь между Cp и CV (уравнение Майера) Cp=CV+R (18). Смысл уравнения ясен из определения понятия Cp (17): для подогрева одного моля газа на один градус при изобарическом процессе потребуется количество теплоты численно равное Cp, часть которого пойдет на увеличение внутренней энергии на величину CV, а остальная часть на совершение одним молем газа работы, численно равной R.
= νR/P подставим в (17)), найдём связь между Cp и CV (уравнение Майера) Cp=CV+R (18). Смысл уравнения ясен из определения понятия Cp (17): для подогрева одного моля газа на один градус при изобарическом процессе потребуется количество теплоты численно равное Cp, часть которого пойдет на увеличение внутренней энергии на величину CV, а остальная часть на совершение одним молем газа работы, численно равной R.
4. Адиабатический процесс (δQ =0). Система в ходе этого процесса изолирована от окружающих тел и не может обмениваться с ними количеством теплоты. Первое начало примет вид: δU=-δA=-PdV (1``), если в условиях адиабатической изолированности газ будет расширяться, то это приведёт к уменьшению его внутренней энергии (dU <0) и, наоборот, процесс совершения работы над газом (по его сжатию, dV <0) будет приводить к повышению внутренней энергии газа (dU >0). Уравнение адиабатического процесса получим, записав уравнение (1``) для одного моля газа (используя (3) и (12)): PdV=-CvdT (19). Затем продифференцируем уравнение Менделеева-Клапейрона для одного моля PdV + VdP = RdT (20). Разделим уравнение (20) на (19) 1+ 
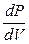 =-
=-  или, используя (17), получим:
или, используя (17), получим:
|
|
|
1+ 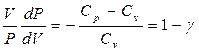 (21), где
(21), где  , перепишем после упрощения последнее уравнение (21) в виде (выполним разделение переменных)
, перепишем после упрощения последнее уравнение (21) в виде (выполним разделение переменных) 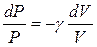 (22), после интегрирования имеем:
(22), после интегрирования имеем: 
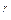 )=ln(const). Тогда уравнение адиабатического процесса примет вид (уравнение Пуассона): PV
)=ln(const). Тогда уравнение адиабатического процесса примет вид (уравнение Пуассона): PV 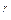 =const (23), где
=const (23), где 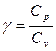 называют показателем адиабаты.
называют показателем адиабаты.
Уравнение адиабаты (23) можно записать и через параметры P и T, если исключить объём из (23), используя уравнение Менделеева-Клапейрона:
P 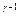 T
T 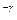 =const (23`)
=const (23`)
Экспериментальный метод определения 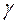 .
.
Рис. 2
В данной работе используется метод адиабатического расширения исследуемого газа (предложен Клеманом и Дезормом). Суть метода в следующем: если в сосуд Б, соединённый с манометром М для измерения давления в сосуде, накачать при закрытом кране К1 небольшую порцию воздуха (2/3 части хода штока насоса Шинца и быстро закрыть кран К2), то при этом газ в сосуде сжимается и нагревается (рис. 2). Для единицы массы воздуха в баллоне этот процесс изображён на P-V диаграмме (рис.3) отрезком адиабаты 1-2. В исходном состоянии объём единицы массы обозначен V1, температура T1 (равна комнатной), давление P1 (равно атмосферному). После накачки воздуха (адиабатическое сжатие) параметры газа Р2, V2, T2. После закрытия кран К2 в сосуде происходит процесс изохорического остывания 2-3 (рис. 3) до начальной температуры (комнатной) T3=T0.
После изохорического остывания (состояние 3, параметры Р3, V3, T3) давление P3 будет несколько выше атмосферного давления на величину Δ P1= Δ h1 , которая измеряется манометром М в мм.вод.ст.: P3 = Pо + Δ P1 (24). Затем открывают кран K1 (на короткий отрезок времени, показание манометра станет равным нулю), происходит процесс адиабатического расширения 3-4 (рис. 3) соответствующий уравнению (22). Как только давление в газе упадет до P0 – атмосферного (состояние 4, параметры Р4 =Р0 , V4, T4) кран K1 закрывается. Далее происходит процесс изохорического нагрева 4-5 до комнатной температуры T5=T0 (состояние 5, параметры Р5, V5, T5), давление при этом будет возрастать P5=Pо+ Δ P2 (25), где ΔP2 = Δh2 измеряется манометром М.

Внешний вид установки
Проанализируем процессы 3-4 и 4-5 подробнее. Процесс 3-4 - адиабатическое расширение и описывается уравнением (23). Поскольку объём выделенной нами единицы массы газа измерить трудно, уравнение адиабаты для 3-4 запишем в виде уравнения (23`): P3 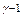 Tо
Tо 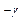 = P4
= P4 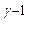 T4
T4  (26). Процесс 4-5 описывается уравнением изохоры (10) или P4T4-1=P5Tо-1 (27). Возведём обе части уравнения (27) в степень γ и поделим уравнение (26) на полученное уравнение (Pγ5Tо-1γ =Pγ4T4-1γ) с целью исключения из этих равенств температур То и Т4 получим:
(26). Процесс 4-5 описывается уравнением изохоры (10) или P4T4-1=P5Tо-1 (27). Возведём обе части уравнения (27) в степень γ и поделим уравнение (26) на полученное уравнение (Pγ5Tо-1γ =Pγ4T4-1γ) с целью исключения из этих равенств температур То и Т4 получим: 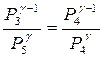 или с учётом Р4=Ро
или с учётом Р4=Ро  (28), учитывая (24) и (25) перепишем (28) в виде:
(28), учитывая (24) и (25) перепишем (28) в виде: 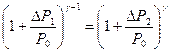 (29).
(29).
Поскольку 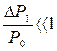 и
и 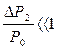 , то с достаточной точностью можно ограничиться только двумя членами в разложении сумм в (29) по степеням γ-1 и γ
, то с достаточной точностью можно ограничиться только двумя членами в разложении сумм в (29) по степеням γ-1 и γ 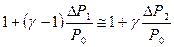 , отсюда уже можно найти значение:
, отсюда уже можно найти значение: 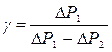 , ΔР измеряется водяным манометром ΔР1=ρgΔh1, ΔP2 = ρgΔh2, где Δh1 и Δh2 разность высот уровней воды в коленах манометра М, соответственно для состояний 3 и 5.
, ΔР измеряется водяным манометром ΔР1=ρgΔh1, ΔP2 = ρgΔh2, где Δh1 и Δh2 разность высот уровней воды в коленах манометра М, соответственно для состояний 3 и 5.
|
|
|
Тогда выражение для расчёта γ будет иметь вид: 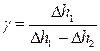 (30).
(30).

Рис. 3
Проведение эксперимента и обработка результатов
До начала эксперимента (краны К1 и К2 открыты) убедитесь в том, что уровни воды в коленах манометра одинаковы, что свидетельствует о том, что давление в сосуде равно атмосферному. Закройте кран К1, а кран К2 подсоедините к насосу и накачайте столько воздуха (1/3 длины штока насоса), чтобы разность уровней столбиков жидкости в манометре Δh 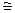 25-30 см. Сразу же закройте кран К2. Поскольку после закрытия крана имеет место процесс изохорического остывания воздуха до комнатной температуры, то следует выждать 1-2 минуты, пока температура газа в сосуде Б наверняка достигнет комнатной. Об этом мы узнаем по установившейся и уже неизменной со временем разности давлении, регистрируемой манометром. Снимите показания манометра Δh1 в мм.вод.ст.
25-30 см. Сразу же закройте кран К2. Поскольку после закрытия крана имеет место процесс изохорического остывания воздуха до комнатной температуры, то следует выждать 1-2 минуты, пока температура газа в сосуде Б наверняка достигнет комнатной. Об этом мы узнаем по установившейся и уже неизменной со временем разности давлении, регистрируемой манометром. Снимите показания манометра Δh1 в мм.вод.ст.
Затем откройте кран К1 и следите по манометру за падением давления воздуха при адиабатическом расширении. Воздух в сосуде при этом охлаждается. Как только уровни воды в коленах манометра выравниваются, кран К1 закройте (в ходе процесса 3-4 кран К1 должен быть перекрыт в момент, когда давление станет равным Ро).
После этого происходит процесс изохорического нагревания газа до комнатной температуры. Давление в сосуде при этом возрастает. Опять надо выждать 1-2 минуты, пока разность давлений не установится неизменной, постоянной и снимите показания манометра Δh2. По формуле (30) рассчитайте значение γ. Опыт повторите не менее 7 раз. После каждого опыта откройте краны К1 и К2 и сделайте выдержку порядка 1 минуты. Результаты измерений занесите в таблицу и рассчитайте погрешность измерений. При подготовке к работе обязательно проработайте указанную литературу.
Контрольные вопросы и задания.
1. Какие процессы, протекающие в газах, называются изохорическими, изобарическими, адиабатическими, изотермическими?
2. Записать уравнение состояния газа для изопроцессов.
3. В чём сущность первого начала термодинамики и какой он принимает вид для всех изопроцессов?
4. Почему теплоёмкость газа при изобарическом процессе больше теплоёмкости этого же газа при изохорическом процессе?
5. В какой последовательности выполняется работа?
6. Почему в данном опыте показатель адиабаты не может быть точно равен величине, рассчитанной в теории, т.е. 1,4?
Литература
1. Сивухин Д.В. Общий курс физики т. 11. – М.: Просвещение, 1975.
2. Яковлев В.Ф., Курс физики (теплота и молекулярная физика). – М.: Просвещение, 1976.
3. Телеснин Р.В., Молекулярная физика. – М.: Просвещение, 1965.
4. Гершезон Е.М., Малов Н.Н., Курс общей физики, Молекулярная физика. - М.: Просв. 1982.
|
|
|


