Главная | Обратная связь | Поможем написать вашу работу!

Вероятность суммы несовместимых событий.

План работы

Вопросы к экзамену. 1

1. Измерение признаков - неметрические шкалы. Ранжирование. 1

2. Метрические шкалы измерения признаков. 3

3. Абсолютная и относительная частота и вероятность случайного события. 4

4. Совместные и несовместные случайные события. Вероятность суммы несовместных событий. 6

5. Зависимые и независимые случайные события. Вероятность произведения независимых случайных событий. 7

6. Дискретные и непрерывные случайные величины. Квантование. 8

7. Гистограмма и полигон распределения случайной величины. 10

8. Меры центральной тенденции, (мода, медиана, среднее арифметическое). 11

9. Виды квантилей. 13

10. Характеристики рассеивания случайной величины (размах, дисперсия, стандартное отклонение, коэффициент вариации). 14

11. Асимметрия и эксцесс распределения случайной величины. 15

12. Свойства нормального распределения случайной величины. 17

13. Стандартное нормальное распределение. Стандартизация распределений. 19

14. Генеральная совокупность и выборка. 19

15. Основные способы формирования выборки. 21

16. Проверка выборки на наличие аномальных значений. 22

17. Основные правила стандартизации психодиагностических методик. 24

18. Шкала Z-оценок. (???) 26

19. Шкалы, производные от шкалы Z-оценок. 27

20. Шкала стенов. 28

Вопросы к экзамену

Измерение признаков - неметрические шкалы. Ранжирование.

с. 16 (23)

Любое эмпирическое научное исследование начинается с того, что исследователь фиксирует выраженность интересующего его свойства (или свойств) у объекта или объектов исследования, как правило при помощи чисел. Таким образом, следует различать объекты исследования (в психологии это чаще всего люди, испытуемые), их свойства (то, что интересует исследователя, составляет предмет изучения) и признаки, отражающие в числовой шкале выраженность свойств.

Измерение в терминах производимых исследователем операций — это приписывание объекту числа по определенному правилу. Это правило устанавливает соответствие между измеряемым свойством объекта и результатом измерения — признаком.

В обыденном сознании, как правило, нет необходимости разделять свойства вещей и их признаки: такие свойства предметов, как вес и длина, мы отождествляем, соответственно, с количеством граммов и сантиметров. Если нет необходимости в измерении, мы ограничиваемся сравнительными суждениями: этот человек тревожный, а этот — нет, этот более сообразителен, чем другой, и т. д.

В научном исследовании нам исключительно важно отдавать себе отчет в том, что точность, с которой признак отражает измеряемое свойство, зависит от процедуры (операции) измерения.

В зависимости от того, какая операция лежит в основе измерения признака, выделяют так называемые измерительные шкалы. Они еще называются шкалами С. Стивенса, по имени ученого-психолога, который их предложил. Эти шкалы устанавливают определенные соотношения между свойствами чисел и измеряемым свойством объектов. Шкалы разделяют на метрические (если есть или может быть установлена единица измерения) и неметрические (если единицы измерения не могут быть установлены).

Номинативная шкала (неметрическая), или шкала наименований (номинальное измерение). В ее основе лежит процедура, обычно не ассоциируемая с измерением. Пользуясь определенным правилом, объекты группируются по различным классам так, чтобы внутри класса они были идентичны по измеряемому свойству. Каждому классу дается наименование и обозначение, обычно числовое. Затем каждому объекту присваивается соответствующее обозначение.

Заметим, что в этом случае мы учитываем только одно свойство чисел — то, что это разные символы. Остальные свойства чисел не учитываются. Привычные операции с числами — упорядочивание, сложение-вычитание, деление — при измерении в номинативной шкале теряют смысл. При сравнении объектов мы можем делать вывод только о том, принадлежат они к одному или разным классам, тождественны или нет по измеренному свойству. Несмотря на такие ограничения, номинативные шкалы широко используются в психологии, и к ним применимы специальные процедуры обработки и анализа данных.

Ранговая, или порядковая шкала (неметрическая) (как результат ранжирования). Как следует из названия, измерение в этой шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства.

Существует множество способов получения измерения в порядковой шкале. Но суть остается общей: при сравнении испытуемых друг с другом мы можем сказать, больше или меньше выражено свойство, но не можем сказать, насколько больше или насколько меньше оно выражено, а уж тем более — во сколько раз больше или меньше. При измерении в ранговой шкале, таким образом, из всех свойств чисел учитывается то, что они разные, и то, что одно число больше, чем другое.

При ранжировании «вручную»', а не при помощи компьютера, следует иметь в виду два обстоятельства:

1. Установите для себя и запомните порядок ранжирования. Вы можете
ранжировать испытуемых по их «месту в группе»: ранг 1 присваивается тому,
у которого наименьшая выраженность признака, и далее — увеличение ранга
по мере увеличения уровня признака. Или можно ранг 1 присваивать тому, у
которого 1-е место по выраженности данного признака (например, «самый
быстрый»). Строгих правил выбора здесь нет, но важно помнить, в каком на
правлении производилось ранжирование.

Соблюдайте правило ранжирования для связанных рангов, когда двое
или более испытуемых имеют одинаковую выраженность измеряемого свой
ства. В этом случае таким испытуемым присваивается один и тот же, средний
ранг. Например, если вы ранжируете испытуемых по «месту в группе» и двое
имеют одинаковые самые высокие исходные оценки, то обоим присваивает
ся средний ранг 1,5: (1+2)/2= 1,5. Следующему за этой парой испытуемому
присваивается ранг 3, и т. д. Это правило основано на соглашении соблюде ния одинаковой суммы рангов для связанных и несвязанных рангов. В соответствии с этим правилом сумма всех присвоенных рангов для группы численностью N должна равняться N(N+\)/2, вне зависимости от наличия или отсутствия связей в рангах.

090309-matmetody.txt

Математичкеские методы в психологии применяются для правильного описания, обобщения и представления получаемых результатов. Математическая обработка данных позволяет выявить и в обобщённом виде записать закономерности психологических явлений. Она нередко способствует пониманию сути и повышает доказательность выводов.

Шкалы.

Математическая обработка данных - это оперирование со значениями какого-либо признака, полученными в результате психологического исследования. Это исследование результатов измерения признаков.

Под измерением признака понимается приписывание объектам или событиям числовых форм в соответствии с определёнными правилами.

Стивенс выделил 4 вида измерения признаков и назвал их шкалами.

1. Первая шкала - номинальная или шкала наименований.

2. Шкала рангов или порядковая шкала.

3. Интервальная шкала.

4. Шкала отношений.

Первые две шкалы - номинальная и ранговая - это неметрические. Две другие - интервальная и отношений - относятся к метрическим.

Номинальная шкала - это способ распределения объектов или явлений по классификационным ячейкам. При использовании шкалы наименований единицей измерений является одно наблюдение. Например, в нашей группе мужчин и женщин можно закодировать, приписав женщинам значение 0, а мужчинам - 1.

Ранговая или порядковая. Эта шкала классифицирует объекты по принципу "больше-меньше". Здесь мы группируем объекты в три и более классов. Придавая значение наименьшего ранга объектам с наименее выраженными свойствами. В порядковой шкале единицей измерений является один ранг. Расстояние между рангами неизвестно - оно может быть одинаковым, а может быть и различным. По ранговой шкале можно выразить, больше или меньше выражено какое-либо свойство. Бегун Иванов прибежал быстрее, чем Сидоров, поэтому у него ранг 1, но насколько Иванов быстрее лучше Сидорова, ранговая шкала не показывает.

Итог. При математической обработке данных, в случае необходимости, всегда можно перейти от шкалы более высокого порядка к шкале более низкого. То есть, если измерен какой-то признак в интервальной шкале, то из этой шкалы легко можно сделать шкалу ранговую или номинальную. Шкала самого высокого порядка - это абсолютная шкала.

2. Метрические шкалы измерения признаков.

с. 19 (26)

Интервальная шкала (метрическая). Это такое измерение, при котором числа отражают не только различия между объектами в уровне выраженности свойства (характеристика порядковой шкалы), но и то, насколько больше или меньше выражено свойство. Равным разностям между числами в этой шкале соответствуют равные разности в уровне выраженности измеренного свойства. Иначе говоря, измерение в этой шкале предполагает возможность применения единицы измерения (метрики). Объекту присваивается число единиц измерения, пропорциональное выраженности измеряемого свойства. Важная особенность интервальной шкалы — произвольность выбора нулевой точки: ноль вовсе не соответствует полному отсутствию измеряемого свойства. Произвольность выбора нулевой точки отсчета обозначает, что измерение в этой шкале не соответствует абсолютному количеству измеряемого свойства. Следовательно, применяя эту шкалу, мы можем судить, насколько больше или насколько меньше выражено свойство при сравнении объектов, но не можем судить о том, во сколько раз больше или меньше выражено свойство.

Интервальные измерения широко используются в психологии. Примером могут являться тестовые шкалы, которые специально вводятся при обосновании равноинтервальности (метричности) тестовой шкалы (IQ Векслера, стены, /"-шкала и т. д.).

Абсолютная шкала, или шкала отношений (метрическая). Измерение в этой шкале отличается от интервального только тем, что в ней устанавливается нулевая точка, соответствующая полному отсутствию выраженности измеряемого свойства.

В силу абсолютности нулевой точки, при сравнении объектов мы можем сказать не только о том, насколько больше или меньше выражено свойство, но и о том, во сколько раз (на сколько процентов и т. д.) больше или меньше оно выражено. Измерив время решения задачи парой испытуемых, мы можем сказать не только о том, кто и на сколько секунд (минут) решил задачу быстрее, но и о том, во сколько раз (на сколько процентов) быстрее.

Следует отметить, что, несмотря на привычность и обыденность абсолютной шкалы, в психологии она используется не часто. Из редких примеров можно привести измерение времени реакции (обычно в миллисекундах) и измерение абсолютных порогов чувствительности (в физических единицах свойств стимула).

Перечисленные шкалы полезно характеризовать еще и по признаку их дифференцирующей способности (мощности). В этом отношении шкалы по мере возрастания мощности располагаются следующим образом: номинативная, ранговая, интервальная, абсолютная. Таким образом, неметрические шкалы заведомо менее мощные — они отражают меньше информации о различии объектов (испытуемых) по измеренному свойству, и, напротив, метрические шкалы более мощные, они лучше дифференцируют испытуемых. Поэтому, если у исследователя есть возможность выбора, следует применить более мощную шкалу. Другое дело, что чаще такого выбора нет, и приходится использовать доступную измерительную шкалу. Более того, часто исследователю даже трудно определить, какую шкалу он применяет.

090309-matmetody.txt

Интервальная шкала основывается на предположении о равенстве разности степени выраженности какого-либо психологического свойства двух объектов, разности двух чисел, приписываемых этим объектам для характеристики свойства. Важная особенность интервальной шкалы - это произвольность выбора нулевой точки. Практически любой психологический тест имеет интервальную шкалу, но она не имеет абсолютного нуля. Например, тест на IQ может показать, насколько Сидоров умнее Иванова, но мы не можем представить себе человека с нулевым интеллектом.

Абсолютная шкала или шкала отношений классифицирует объекты или субъекты пропорционально степени выраженности измеряемого свойства, то есть предполагает равенство отношения степени выраженности какого-либо психологического свойства двух объектов отношению двух чисел, приписываемых этим объектам для характеристики свойства. Принципиальная разница между шкалой интервалов и шкалой отношений заключается в том, что в интервальной шкале нет абсолютного нуля, и нулевая точка ставится условно, а в шкале отношений такая точка есть.

3. Абсолютная и относительная частота и вероятность случайного события.

090309-matmetody.txt

Случайным событием называется любое событие, которое может произойти или не произойти в результате некоторых действий. Числовыми мерами появления случайного события являются абсолютная частота, относительная частота и вероятность.

Абсолютная частота - это количество событий, интересующих исследователя. Абсолютную частоту принятно обозначать буквой F с индексом i (или каким-нибудь другим, например a)

Относительная частота - это абсолютная частота, отнесённая к общему количеству событий в некотором опыте (рис. 1 в тетради).

Вероятность - это то значение, к которому стремится относительная частота при бесконечном увеличении числа опытов.

081128-matmetody.txt

Случайным событием называется такой исход эксперимента или наблюдения, кооторый при реализации данного комплекса условий может произойти, а может и не произойти.

Достоверное событие - такое событие, которое при реализации данного комплекса условий непременно произойдёт.

Невозможное событие - такое событие, которое при реализации данного комплекса условий заведомо не может произойти.

Выпадение одного из перечисленных числа очков является элементарным.

Отношения между событиями.

Сопоставим события: событие А - появление герба при подбрасывании монеты. Событие бэ - непоявление цифры при подбрасывании монеты. Следовательно а и бэ - равносильные события (а включает бэ, а бэ включает а).

Два события а и бэ, произведение которых является невозможным событием, являются несовместимыми.

Суммой двух несовместимых событий а и бэ называется событие цэ, осуществляющееся в появлении либо события а, либо события бэ.

Если сумма событий а и бэ - событие достоверное, а произведение событий - невозможное, то такие события называются противоположными.

Если ни одно из элементарных событий данного множества не является объективно более возможным, чем другое, то такие события называются равновозможными.

Вероятность события.

Пусть эМ - число равновозможных элементарных событий, которые благоприятствуют появлению некоторого события А. Эн - число элементарных событий, образующих полную группу равновозможных и попарно несовместимых событий. Отношение эМ к эН назовём вероятностью события А и обозначим (формула в тетради - вероятность события А равна отношению событий эМ к эН).

Вероятность любого события лежит от 0 до единицы. 0 - невозможность события, а 1 - 100% вероятность того, что это событие произойдёт.

komb-teorver-stat.htm

Событием называют возможный результат эксперимента. Событие может
содержать в себе один или несколько элементарных исходов и может рассматриваться как
подмножество множества элементарных исходов.

Все события можно разделить на 2 группы: события детерминированные и события
случайные.

Случайное событие - это событие, про которое заранее неизвестно, произойдет оно
или не произойдет в данном комплексе условий. Например, выпадение герба при
подбрасывании монеты. Случайные события принято обозначать заглавными начальными
буквами латинского алфавита: А, В, С...

Вероятность случайного события - это число, которое характеризует возможность
появления данного события в эксперименте. Обозначается она буквой р (от
французского probabilite - вероятность). Существуют различные способы определения
этого понятия.

Классическое определение вероятности. Если опыт, в котором может наступить
событие А имеет конечное число исходов, причем эти исходы равновозможны, то

вероятность события А вычисляется по формуле: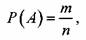где п - общее число

элементарных исходов, т - число элементарных исходов, благоприятствующих событию
А.

Статистическое определение вероятности связано с понятием относительной
частоты события. Относительной частотой события А называют отношение числа
испытаний, в которых наступило событие А к общему числу проведенных испытаний:

Относительная частота обладает свойством статистической устойчивости;

при проведении серий с большим количеством испытаний относительные частоты будут
группироваться вокруг некоторого числа. Это число и будет являться статистической
вероятностью события А.

4. Совместные и несовместные случайные события. Вероятность суммы несовместных событий.

081128-matmetody.txt

Отношения между событиями.

Два события а и бэ, произведение которых является невозможным событием, являются несовместимыми.

Вероятность суммы несовместимых событий.

Вероятность суммы попарно несовместимых событий равна сумме вероятности этих событий (формулы в тетради).

Вероятность суммы двух совместимых событий равна сумме вероятностей этих событий без вероятностей их совместного осуществления (формулы в тетради). То есть, если события А и Бэ совместимы, то... формула в тетради.

komb-teorver-stat.htm

События А и В называются несовместными, если в результате испытания
они никогда не могут наступить вместе (например, выпадение 3 и 6 при подбрасывании
кубика). Несовместные события не содержат в себе общих элементарных исходов.

События А и В называются совместными, если в результате испытания они
могут наступитьвместе(например,выпадениечетногочисла очковичисла очков,
кратного трем, при подбрасывании кубика). Совместные события содержат в себе общие
элементарные исходы.

Суммой событий А и В называется событие С, которое состоит либо в наступлении события А, либо в наступлении события В, либов их одновременном наступлении. Обозначается С=А+В

5. Зависимые и независимые случайные события. Вероятность произведения независимых случайных событий.

komb-teorver-stat.htm

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Определение: Вероятность события А, вычисленная при условии, что событие В произошло называется условной вероятностью событияА относительно события В и обозначается

Определение. Событие А называется независимым от события В, если вероятность события А не зависит от того произошло событие В или нет, то есть

Теорема 3. Вероятность произведения (совместного появления) двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную

при условии, что первое событие уже наступило:

Следствие. Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего события вычисляется при условии, что все предыдущие имели место:

Теорема 4. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Следствие. Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:

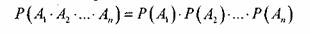
081128-matmetody.txt

Вероятность произведения событий А и Бэ равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое событие произошло.

Вероятность произведения события А и Бэ, если события А и Бэ независимы, равна произведению вероятностей этих событий.

6. Дискретные и непрерывные случайные величины. Квантование.

090309-matmetody.txt

Случайной величиной называется такая переменная величина, которая принимает значение из некоторого множества. Принято выделять дискретные и непрерывные случайные величины.

Дискретная случайная величина принимает свои значения из множества целых чисел. Например, количество студентов данной группы.

Непрерывная случайная величина принимает свои значения из множества действительных чисел.

Операции.

Разбиение числовой оси на равные интервалы называется квантованием, а полученные интервалы - интервалами квантования. Например, возраст - мы измеряем интервалом, равным одному году. Ряд различных психологических явлений мы измеряем квантованием.

Основной способ описания случайной величины - это построение её распределения.

Для дискретной величины подсчитывают количество случаев, приходящихся на каждое значение, то есть абсолютную частоту, затем строят гистограмму или столбчатую диаграмму, которая наглядно представляет особенности распределения.

Есть ещё некоторые показатели, которые так или иначе делят выборку.

Квантили - такие значения случайной величины, которые делят распределения на равные части. Их существует несколько видов.

1. Квартили - делят выборку на четыре равные части - по 25% на каждую часть.

2. Квинтили - делять выборку на 5 равных частей - по 20% на каждую часть.

3. Децили - делят выборку на 9 частей, то есть, девять децилей делят выборку на десять равных частей по 10% на каждую часть.

4. Процентили - 99 процентилей делят выборку на 100 равных частей по 1%. Процентили нельзя путать с процентами. Процентные показатели - это первичные показатели, которые определяют, например, количество правильно выполненных заданий. А процентиль - показатель производный, указывающий да долю от общего числа членов группы.

komb-teorver-stat.htm

Наряду со случайными событиями одним из основных понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется величина, принимающая в результате испытания некоторое, наперед неизвестное значение, которое может изменяться от испытания к испытанию. Случайные величины принято обозначать 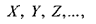их возможные

значения -

Случайные величины могут классифицироваться следующим образом:

• Величины количественные и качественные. Количественные величины
называются также числовыми.

• Величины одномерные и многомерные.

• Величины дискретные и непрерывные (для числовых величин).

§1. Дискретная случайная величина. Закон распределения вероятностей дискретной случайной величины

Дискретной случайной величиной называется случайная величина, принимающая отдельные, изолированные друг от друга значения. Возможные значения дискретной случайной величины образуют или конечное множество (например, X - случайная величина, равная числу очков, выпавшему на верхней грани кубика, возможны 6 различных значений) или счетное множество (бесконечное множество, элементы которого можно пронумеровать; например, X - случайная величина, равная количеству подбрасываний монеты до первого выпадения герба).

Для задания случайной величины недостаточно знать только ее возможные значения. Две случайные величины могут иметь одинаковые значения, но принимать их с различными вероятностями (например, оценки на экзамене у сильных и слабых студентов). Поэтому необходимо указать и возможные значения, и их вероятности.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями это величины и их вероятностями.

Закон распределения может быть задан тремя способами:

1) Табличный способ - в первой строке таблице в порядке возрастания перечисляются возможные значения случайной величины, во второй - их вероятности.

В данной таблице /?, - вероятность того, что случайная величина X приняла значение причем сумма вероятностей в нижней строке должна быть

равна единице: Такую таблицу называют рядом распределения вероятностей

дискретной случайной величины.

2) Графический способ - по оси абсцисс откладываются возможные значения
случайной величины, по оси ординат - их вероятности. Полученные точки соединяются
отрезками. Такой график называют полигоном распределения.

3) Аналитический способ - соответствие между значениями случайной величины и
их вероятностями задается с помощью формулы:

§2. Непрерывная случайная величина, способы ее задания

Непрерывной случайной величиной называется случайная величина, принимающая любое значение из некоторого конечного или бесконечного промежутка (например, время работы прибора до его поломки, размер детали и т.п.). Количество значений непрерывной случайной величины бесконечно, невозможно перечислить все ее возможные значения, поэтому необходимы другие способы ее задания.

Распределение вероятностей непрерывной случайной величины может быть задано двумя способами: с помощью функции распределения вероятностей и с помощью плотности распределения вероятностей.

Функцией распределения вероятностей случайной величины называется функция, равна в каждой точке х вероятности того, что случайная величина примет значение меньшее, чем

Плотностью распределения вероятностей случайной величины называется производная от функции распределения вероятностей:

Функция распределения вероятностей может быть задана как для дискретной случайной величины, так и для непрерывной, а плотность распределения вероятностей задается только для непрерывной случайной величины. Одним из важных свойств

плотности распределения вероятностей является условие нормировки:

Плотность распределения вероятностей называют также законом распределения непрерывной случайной величины.

7. Гистограмма и полигон распределения случайной величины.

090309-matmetody.txt

Гистограмма - это столбиковоя диаграмма, каждый столбец которой опирается на конкретное значение признака или разрядный интервал.

Построение полигона распределения частот напоминает построение гистограммы - когда верхние точки столбцов гистограммы соединяются отрезками (получается ломаная линия).

Вместо гистограммы и полигона часто изображают сглаженную кривую распределения частот.

с. 27 (34)

Гистограмма распределения частот — это столбиковая диаграмма, каждый столбец которой опирается на конкретное значение признака или разрядный интервал (для сгруппированных частот). Высота столбика пропорциональна частоте встречаемости соответствующего значения. На рис. 3.1 изображена гистограмма распределения частот для примера из табл. 3.2.

Гистограмма накопленных частот отличается от гистограммы распределения тем, что высота каждого столбика пропорциональна частоте, накопленной к данному значению (интервалу).

Построение полигона распределения частот напоминает построение гистограммы. В гистограмме вершина каждого столбца, соответствующая частоте встречаемости данного значения (интервала) признака, — отрезок прямой. А для полигона отмечается точка, соответствующая середине этого отрезка. Далее все точки соединяются ломаной линией (рис. 3.3).

Вместо гистограммы или полигона часто изображают сглаженную кривую распределения частот. На рис. 3.4 изображена гистограмма распределения для примера из табл. 3.3 (столбики) и сглаженная кривая того же распределения частот.

8. Меры центральной тенденции, (мода, медиана, среднее арифметическое).

090309-matmetody.txt

Параметры распределения.

Распределение случайной величины характеризуется парамерами распределения, которые объединены в группы характеристик:

1. характеристики положения;

2. характеристики рассеивания;

3. характеристики ассиметрии;

4. характеристики эксцесса.

В характеристики полжения входят - мода, медиана и среднее арифметическое значение. По-другому три эти характеристики называются мерами центральной тенденции.

Мода - это наиболее часто встречающееся распределение признака, обозначается буквой M с индексом o. Его ещё называют модальное значение. Ещё есть модальный интервал - так именуется интервал, куда попадает наибольшее количество значений. Чаще всего модальное значение бывает в модальном интервале.

Распределение величины может быть унимодальным и полимодальным. Унимодальное распределение - если мода в распределении одна. Если больше, то распределение называется полимодальным.

Среднее арифметическое значение - обозначается буквой M с индексом x и считается по формуле (рис. 3 в тетради - не успела зарисовать)

Медиана - такое значение случайной величины, которое делит упорядоченную в порядке возрастания или убывания выборку пополам. Обозначается буквой M с индексом e. При нечётном количестве случайных величин за медиану принимается непосредственно центральное значение. Если число значений случайной величины в выборке чётное, то медиана оказывается между двумя значениями. В этом случае значение медианы рассчитывается как среднее арифметическое между ними. На кривой распределения значение медианы всегда распологается между значениями моды и среднего арифметического.

с. 33 (40)

Мера центральной тенденции {Central Tendency) — это число, характеризующее выборку по уровню выраженности измеренного признака.

Существуют три способа определения «центральной тенденции», каждому из которых соответствует своя мера: мода, медиана и выборочное среднее.

Мода {Mode) — это такое значение из множества измерений, которое встречается наиболее часто. Моде, или модальному интервалу признака, соответствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.

Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений.

Распределение может иметь и не одну моду. Когда все значения встречаются одинаково часто, принято считать, что такое распределение не имеет моды.

Бимодальное распределение имеет на графике распределения две вершины, даже если частоты для двух вершин не строго равны. В последнем случае выделяют большую и меньшую моду. Во всей группе может быть и несколько локальных вершин распределения частот. Тогда выделяют наибольшую моду и локальные моды.

Еще раз отметим, что мода — это значение признака, а не его частота.

Медиана {Median) — это такое значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:

□ если данные содержат нечетное число значений (8, 9, 10, 13, 15), то ме
диана есть центральное значение, т. е. Md= 10;

□ если данные содержат четное число значений (5, 8, 9, 11), то медиана
есть точка, лежащая посередине между двумя центральными значения
ми, т. е. М/=(8+9)/2 = 8,5.

Среднее (Mean) (М_х — выборочное среднее, среднее арифметическое) — определяется как сумма всех значений измеренного признака, деленная на количество суммированных значений.

Если некоторый признак X измерен в группе испытуемых численностью N, мы получим значения: х_и х₂,..., x_h..., x_N (где / — текущий номер испытуемого, от 1 до N). Тогда среднее значение М_х определяется по формуле:

М_х= — Ух,. (4.1)

Свойства среднего. Если к каждому значению переменной прибавить одно и то же число с, то среднее увеличится на это число (уменьшится на это число, если оно отрицательное):

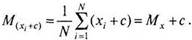1 ^N ^(*,₊O=-^-I>;+c) = M_x+c. ₍₄.2)

А если каждое значение переменной умножить на одно и то же число с, то среднее увеличится в с раз (уменьшится в с раз, если делить на с):

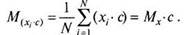M_(XrC)=^i(x_rc)=M_x-c. (4.3)

Далее мы неоднократно будем обращаться к такой величине, как отклонение от среднего: (*,•— М_х). Из первого, очевидного свойства среднего следует

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

еще одно важное свойство, не столь очевидное: сумма всех отклонений от среднего равна нулю:

£(*,.-Л/_х) = 0. (4.4)

Соответственно, среднее отклонение от среднего также равно 0.

9. Виды квантилей.

090309-matmetody.txt

Есть ещё некоторые показатели, которые так или иначе делят выборку.

1. Квартили - делят выборку на четыре равные части - по 25% на каждую часть.

2. Квинтили - делять выборку на 5 равных частей - по 20% на каждую часть.

Воспользуйтесь поиском по сайту: