Главная | Обратная связь | Поможем написать вашу работу!

способ (по формуле классической вероятности)

З А Д А Н И Я

по теме " Случайные события"

1. В партии из n деталей имеется k стандартных. Наудачу взяли m деталей. Найти вероятность того, что среди отобранных хотя бы одна нестандартная.

вар.	n	k	m	вар.	n	k	m

2. Среди ста лотерейных билетов есть n выигрышных. Найти вероятность того, что m наудачу выбранных билета окажутся выигрышными.

Указания. Задачи 1 и 2 решить двумя способами: 1) используя формулу классической вероятности; 2) используя теорему умножения вероятностей.

вар.	n	m	вар.	n	m

3. Станок состоит из трех независимо работающих деталей. Вероятность отказа деталей соответственно равна p₁, p₂, p₃. Найти 1) вероятность поломки станка, если для этого достаточно отказа хотя бы одной детали 2) вероятность, отказа одной детали.

вар.	p₁	p₂	p₃	вар.	p₁	p₂	p₃
	0,3	0,1	0,2		0,25	0,1	0,2
	0,4	0,3	0,2		0,4	0,4	0,2
	0,5	0,1	0,3		0,3	0,1	0,3
	0,3	0,2	0,4		0,7	0,2	0,4
	0,6	0,1	0,2		0,2	0,1	0,8
	0,3	0,1	0,6		0,4	0,1	0,6
	0,2	0,4	0,7		0,3	0,4	0,2
	0,3	0,1	0,5		0,5	0,1	0,3
	0,4	0,6	0,2		0,6	0,1	0,2
	0,3	0,1	0,1		0,2	0,1	0,8

4. Из партии изделий товаровед выбирает изделия высшего сорта. Вероятность, что изделие окажется высшего сорта равна р. Найти вероятность, что из n проверенных изделий только k изделий высшего сорта.

вар.	p	n	k	вар.	p	n	k
	0.8				0.8
	0.9				0.9
	0.75				0.7
	0.95				0.88
	0.7				0.86
	0.85				0.92
	0.9				0.79
	0.6				0.87
	0.75				0.96
	0.95				0.86

5. Сборщик получил три коробки деталей, изготовленных первым заводом и 2 коробки деталей, изготовленных вторым заводом. Вероятность того, что деталь с первого завода отличного качества, равна р1, а со второго завода - p2. Найти вероятность того, что извлечена деталь отличного качества.

вар.	p₁	p₂	вар.	p₁	p₂
	0.88	0.90		0.89	0.92
	0.76	0.98		0.97	0.87
	0.75	0.96		0.85	0.78
	0.98	0.85		0.95	0.75
	0.90	0.88		0.79	0.90
	0.89	0.79		0.78	0.97
	0.79	0.90		0.85	0.78
	0.88	0.96		0.87	0.67
	0.97	0.78		0.91	0.65
	0.95	0.78		0.95	0.75

6. Два контролера проверяют изделия на стандартность. Производительность труда второго контролера в полтора раза больше, чем первого. Вероятность, что стандартное изделие будет признано стандартным первым контролером, равна р₁, а вторым - р₂. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил k -тый контролер.

вар.	p₁	p₂	k	вар.	p₁	p₂	k
	0.99	0.78			0.89	0.78
	0.98	0.87			0.87	0.95
	0.80	0.78			0.96	0.80
	0.95	0.76			0.86	0.75
	0.85	0.76			0.88	0.90
	0.78	0.90			0.95	0.80
	0.97	0.88			0.92	0.90
	0.89	0.97			0.91	0.75
	0.87	0.99			0.90	0.80
	0.89	0.90			0.80	0.97

7. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди n новорожденных:

а) не менее k1 и не более k2 мальчиков;

б) не менее k2 мальчиков.

вар.	n	k₁	к₂	вар.	n	k₁	к₂

Решение типового варианта заданий по теме "Случайные события"

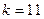Задание 1. В партии из деталей имеется стандартных. Наудачу взяли деталей. Найти вероятность того, что среди отобранных деталей есть хотя бы одна нестандартная.

Решение

Способ (по формуле классической вероятности)

Пусть событие А состоит в том, что среди отобранных деталей есть хотя бы одна нестандартная.

Противоположное событие - среди извлечённых деталей все оказались стандартными.

Общее число возможных элементарных исходов равно числу способов, которыми можно извлечь в партии из , т.е. числу сочетаний из по : .

Найдём число исходов, благоприятствующих интересующему нас событию: среди извлечённых деталей все оказались стандартными. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать детали из 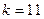стандартных, т.е. .

Вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу элементарных исходов

Искомая вероятность равна

2 способ. Найдем по теореме умножения вероятностей.

Пусть - i-тая деталь является стандартной. Произведение событий , i=1,2,3,4 это событие, состоящее в том, что все 4 детали являются стандартными.

Ответ:

Задание 2. Среди ста лотерейных билетов есть выигрышных. Найти вероятность того, что наудачу выбранных билетов окажутся выигрышными.

Решение

способ (по формуле классической вероятности)

Общее число возможных элементарных исходов равно числу способов, которыми можно извлечь из лотерейных билетов, т.е. числу сочетаний из по : .

Найдём число исходов, благоприятствующих интересующему нас событию: среди извлечённых лотерейных билетов все оказались выигрышными. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать лотерейных билетов из выигрышных, т.е. .

Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу элементарных исходов

2 способ. Найдем по теореме умножения вероятностей. Пусть - i-тый билет выигрышный. Произведение событий , i=1,2,3,4 это бытие, состоящее в том, что все 4 билета являются выигрышными.

Задание 3. Станок состоит из трех независимо работающих деталей. Вероятность отказа деталей соответственно равна p₁=0,3, p₂ =0,2, p₃ =0,1. Найти 1) вероятность поломки станка, если для этого достаточно отказа хотя бы одной детали 2) вероятность отказа одной детали.

Решение 1) Пусть событие состоит в том, что i-тая деталь отказала. Тогда вероятность поломки станка, т.е. вероятность отказа хотя бы одной детали найдем через противоположное событие – все три детали работают.

2) вероятность отказа одной детали равна

Задание 4. Из партии изделий товаровед выбирает изделия высшего сорта. Вероятность, что изделие окажется высшего сорта равна . Найти вероятность, что из проверенных изделий только изделий высшего сорта.

Решение

По условию задачи вероятность извлечения изделия высшего сорта можно считать одинаковой в испытаниях; . Используя формулу Бернулли, получаем:

Задание 5. Сборщик получил три коробки деталей, изготовленных первым заводом и две коробки деталей, изготовленных вторым заводом. Вероятность того, что деталь с первого завода отличного качества, равна 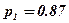, а со второго завода — . Найти вероятность того, что извлечена деталь отличного качества.

Решение

Введём обозначения событий:

Событие — извлечённая деталь отличного качества;

Событие — извлечённая деталь изготовлена первым заводом;

Событие — извлечённая деталь изготовлена вторым заводом.

По условию задачи:

(вероятность того, деталь, изготовленная на первом заводе отличного качества);

(вероятность того, деталь, изготовленная на втором заводе отличного качества);

(вероятность того, что наудачу извлечённая деталь изготовлена на первом заводе);

(вероятность того, что наудачу извлечённая деталь изготовлена на втором заводе).

По формуле полной вероятности находим, что вероятность того, что наудачу извлеченная деталь отличного качества равна:

Задание 6. Два контролёра проверяют изделия на стандартность. Производительность труда второго контролёра в полтора раза выше, чем первого. Вероятность, что стандартное изделие будет признано стандартным первым контролёром, равна , а вторым — . Найти вероятность того, что это изделие проверил первый контролёр.

Решение

Введём обозначения событий:

— стандартное изделие признано контролёром стандартным;

— изделие проверялось первым контролёром;

— изделие проверялось вторым контролёром.

По условию задачи вероятность того, что стандартное изделие будет признано стандартным при проверке первым контролёром , а вторым — . Поскольку производительность труда второго контролёра в полтора раза выше, чем первого, то , а т.к. события и образуют полную группу, то , поэтому 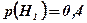, а .

Вероятность того, что стандартное изделие проверил первый контролёр и признал его годным, найдём по формуле Бейеса:

Задание 7. Вероятность рождения мальчика равна . Найти вероятность того, что среди новорождённых:

а) не менее и не более мальчиков;

б) не менее мальчиков.

Решение

Воспользуемся интегральной теоремой Лапласа:

где — функция Лапласа,

а) По условию, Вычислим

Таким образом, вероятность того, что среди новорождённых не менее и не более мальчиков равна

б) Требование, чтобы событие появилось не менее раз, означает, что число появлений события может быть равно 70, либо 71, …, либо 125. Таким образом, в рассматриваемом случае следует принять Тогда

Таким образом, вероятность того, что среди новорождённых не менее мальчиков равна

т.е. вероятность события, в котором среди новорождённых не менее мальчиков равна 0,1314.

Задача 8

Варианты1-5

;

Варианты 6-10

;

Варианты 11-15

;

Варианты 16-20

;

Варианты 21-25

;

Воспользуйтесь поиском по сайту: