 |
К вопросу об эксперименте Эйнштейна – де Гааза
|
|
|
|
РИС.19-1
Правило правой руки.
Стрелка под проводом. Если стрелка над проводом, то направление поворота меняется на обратное. Эффект наблюдается во всех случаях при протекании тока, независимо от природы проводника (например, ионный ток в электролите). Два провода, по которым текут токи – взаимодействуют: опыты Ампера в том же 1820 г.
Взаимодействие проводников с током, контуров с током, соленоидов и т.п. подобно действию токов на магниты и называется магнитным взаимодействием. Зависит не от зарядов, а от токов. Не экранируется проводниками.
{Магнитное поле (постоянное), в свою очередь, действует на заряды: электронно-лучевая трубка, кинескоп, ускорители, масс-спектрометры.}
Закон магнитного взаимодействия токов
Что установлено экспериментально? (главным образом – А. М. Ампером-1775-1836)
1. Сила взаимодействия двух проводников пропорциональна силе тока в каждом из них:  .
.
2. Изогнутый провод с током не оказывает магнитного действия (равно как и скрученный).
Бифилярная намотка: одна часть провода произвольно навита вокруг другой.
Отсюда следует, что элементы проводника с током  оказывают такое же магнитное действие, как элемент (отрезок)
оказывают такое же магнитное действие, как элемент (отрезок)  , их замыкающий.
, их замыкающий.
 |
РИС.19-2
Итак: магнитное действие бесконечно малого отрезка проводника с током определяется произведением  , где
, где  - сила тока, а
- сила тока, а  - вектор, имеющий длину отрезка
- вектор, имеющий длину отрезка  и направленный вдоль тока.
и направленный вдоль тока.
 - элемент тока (линейный элемент тока).
- элемент тока (линейный элемент тока).
Отсюда:  .
.
3. Ампер установил, что сила взаимодействия обратно пропорциональна квадрату расстояния между элементами тока:  .
.
4. Величина и направление силы взаимодействия двух элементов с током зависят от их взаимной ориентации (выявление этой зависимости было наиболее трудным экспериментально).
|
|
|
Из опыта (Рис. 19-3) следует, что  не оказывает никакого действия на
не оказывает никакого действия на  , поэтому сила, действующая на
, поэтому сила, действующая на  ,
,  , где
, где 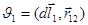 .
.
Если  и
и  не лежат в одной плоскости, то отрезок
не лежат в одной плоскости, то отрезок  можно разложить на две составляющие:
можно разложить на две составляющие:  - в плоскости, содержащей
- в плоскости, содержащей  и
и  ,
,
 - перпендикулярно этой плоскости.
- перпендикулярно этой плоскости.
Сила, действующая на  , всегда равна нулю. Сила, действующая на
, всегда равна нулю. Сила, действующая на  , пропорциональна
, пропорциональна  , где
, где  - направление нормали к плоскости (Рис. 19-4).
- направление нормали к плоскости (Рис. 19-4).
Итак, экспериментально установленный закон взаимодействия проводников с током
(основной закон в учении о магнетизме -закон Ампера):

(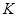 - коэффициент пропорциональности, зависящий от выбора системы единиц).
- коэффициент пропорциональности, зависящий от выбора системы единиц).
 |
РИС.19-3
 |
РИС.19-4
Направление силы 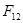 - она перпендикулярна элементу
- она перпендикулярна элементу  и лежит в плоскости, содержащей
и лежит в плоскости, содержащей  и
и  .
.
Иначе: правило правого буравчика (штопора): если вращать правый буравчик так, чтобы рукоятка перемещалась от элемента  к нормали
к нормали  , то поступательное движение буравчика совпадет с направлением силы
, то поступательное движение буравчика совпадет с направлением силы 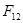 .
.
Направление нормали  - задается тем же правилом: оно совпадает с поступательным движением буравчика, если его вращать от элемента
- задается тем же правилом: оно совпадает с поступательным движением буравчика, если его вращать от элемента  к радиусу - вектору
к радиусу - вектору  .
.
В векторной форме закон Ампера:
 .
.
Напряженность магнитного поля  вводим по аналогии с напряженностью электрического поля
вводим по аналогии с напряженностью электрического поля  из сопоставления закона Кулона и закона Ампера.
из сопоставления закона Кулона и закона Ампера.
| Кулон | Ампер |

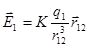

| 

 Роль заряда играет линейный элемент тока
Роль заряда играет линейный элемент тока  . Движущиеся заряды! . Движущиеся заряды!
|
Напряженность магнитного поля определяется путем интегрирования по всему контуру с током: 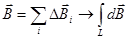 .
.
Примеры
Магнитное поле в центре кругового проводника
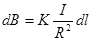 , т.к.
, т.к.  и расстояния все одинаковые и равны
и расстояния все одинаковые и равны  .
.
 .
.
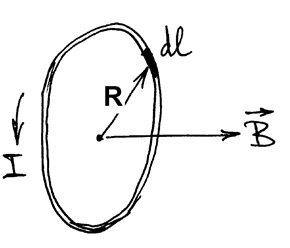 |
РИС.19-5
 |
Магнитное поле прямого тока
РИС.19-6
Провод бесконечный. Направление магнитного поля для всех элементов провода одинаковые, поэтому складываем абсолютные значения  .
.
|
|
|
 ,
,
 ,
,  .
.
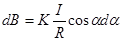 Þ
Þ 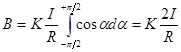 .
.
Единицы  -Тл (SI).
-Тл (SI).
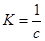 - в CGSE,
- в CGSE,
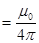 в SI.
в SI.
 ;
; 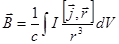 .
.
Сила Лоренца, действующая на точечный заряд  , движущийся со скоростью
, движущийся со скоростью 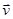 (постоянной) в электрическом поле
(постоянной) в электрическом поле 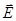 и магнитном поле
и магнитном поле  :
:
 .
.
Если по некоторому объема проводника 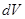 протекает ток
протекает ток  , а этот элемент находится в магнитном поле
, а этот элемент находится в магнитном поле  , то на этот элемент действует сила
, то на этот элемент действует сила  - это прямое следствие из магнитной составляющей силы Лоренца.
- это прямое следствие из магнитной составляющей силы Лоренца.
Плотность пондеромоторных сил:
 .
.
Закон Био-Савара-Ампера
Если точечный заряд движется со скоростью (постоянной) 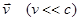 , то напряженность магнитного поля, создаваемого этим зарядом в точке наблюдения, определяемой радиусом-вектором
, то напряженность магнитного поля, создаваемого этим зарядом в точке наблюдения, определяемой радиусом-вектором  :
:
 .
.
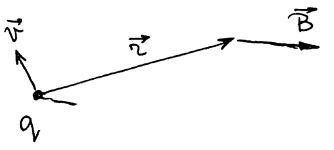 |
РИС.19-7
Нам известно, что напряженность поля точечного заряда  , следовательно, можно записать:
, следовательно, можно записать:  .
.
Воспользовавшись принципом суперпозиции (каждый заряд создает магнитное поле совершенно независимо от всех остальных зарядов), находим:
 .
.
Связь объемных и линейных токов 
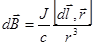
 .
.
Поскольку выделить элемент объемного тока  или элемент линейного тока
или элемент линейного тока  на практике невозможно, то опытной проверке могут быть подвергнуты лишь интегральные соотношения (закон Био-Савара в 1820 г.):
на практике невозможно, то опытной проверке могут быть подвергнуты лишь интегральные соотношения (закон Био-Савара в 1820 г.):
 (
( не зависит от времени),
не зависит от времени),
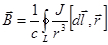 (
(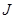 не зависит от времени).
не зависит от времени).
Эти выражения справедливы только для замкнутых токов, каковыми и являются токи постоянные.
Вектор-потенциал магнитного поля
Одно из основных уравнений магнитного поля  можно записать в более удобной форме.
можно записать в более удобной форме.
Подынтегральная функция:
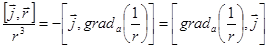 (
( - по точке наблюдения).
- по точке наблюдения).
Рассмотрим выражение для дифференцирования произведения скаляра и вектора:
 ,
,
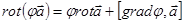 .
.
Отсюда: 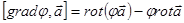 .
.
Подставим  ,
,  :
:
 .
.
Рассмотрим теперь  и покажем, что
и покажем, что  , так как значение вектора плотности тока не зависит от перемещения точки наблюдения. Действительно:
, так как значение вектора плотности тока не зависит от перемещения точки наблюдения. Действительно:
 , где
, где  - координаты точки истока.
- координаты точки истока.
 .
.
Рассмотрим любую компоненту  , например, компоненту
, например, компоненту  :
:
 .
.
Таким образом, подынтегральная функция в законе Био-Савара стала:  .
.
Закон Био-Савара приобрел вид:  .
.
В этом выражении дифференцирование. т.е. образование ротора, производится по координатам точки наблюдения ( ), а интегрирование – по объему проводников, обтекаемых током. Эти операции можно поменять местами:
), а интегрирование – по объему проводников, обтекаемых током. Эти операции можно поменять местами:
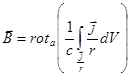 .
.
Если ввести обозначение:
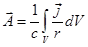 , то уравнение примет вид:
, то уравнение примет вид:
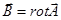 , где индекс «
, где индекс « » при знаке ротора опущен как излишний, так как при заданном распределении токов вектор
» при знаке ротора опущен как излишний, так как при заданном распределении токов вектор  зависит только от положения точки наблюдения.
зависит только от положения точки наблюдения.
|
|
|
Напряженность магнитного поля  может быть представлена в виде ротора некоторого вектора
может быть представлена в виде ротора некоторого вектора  , который называется вектор-потенциалом токов.
, который называется вектор-потенциалом токов.
Вектор-потенциал объемных токов: 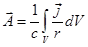 .
.
Вектор потенциал линейных токов, т.е. на расстояниях от токов - больших по сравнению с размерами их сечения:  .
.
Аналогия между скалярным потенциалом стационарной системы точечных зарядов  и векторным потенциалом системы постоянных токов
и векторным потенциалом системы постоянных токов  :
:

| 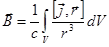
|
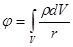
| 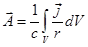
|

| 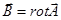
|
Из этого сопоставления следует,
что вектор плотности тока  играет для магнитного поля такую же роль, как скаляр плотности зарядов
играет для магнитного поля такую же роль, как скаляр плотности зарядов  для электростатического поля.
для электростатического поля.
Дифференциальные соотношения для вектор-потенциала 
(дополнительный материал)
В электростатике мы получили уравнение Пуассона
 , решением которого было
, решением которого было 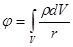 .
.
Запишем аналогичные выражения для компонент вектор-потенциала:
 Þ
Þ  ;
;
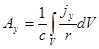 Þ
Þ 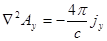 ;
;
 Þ
Þ  .
.
Правые три уравнения для компонент вектора эквивалентны одному векторному уравнению 
 ,
,
которое и является искомым дифференциальным уравнением для векторного потенциала.
Это уравнение справедливо, если
1) сам вектор-потенциал и его пространственные производные конечны и непрерывны во всем исследуемом пространстве;
2) при 
 и
и  ®0 или хотя бы остаются конечными.
®0 или хотя бы остаются конечными.
Рассмотрим  .
.
 (
(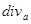 - по координатам точки наблюдения).
- по координатам точки наблюдения).
Порядок дифференцирования по координатам точки наблюдения и интегрирования по объемам, обтекаемым точками, может быть изменен на обратный:
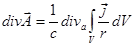 ,
,
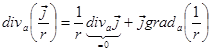 (
( , так как вектор плотности тока зависит только от координат истока, а не от координат точки наблюдения).
, так как вектор плотности тока зависит только от координат истока, а не от координат точки наблюдения).
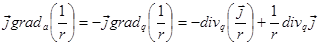 .
.
 - в силу замкнутости постоянных токов.
- в силу замкнутости постоянных токов.
Следовательно, 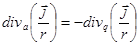 .
.
 .
.
Последний интеграл можно преобразовать по теореме Гаусса, так как пространственное интегрирование в нем происходит по тем же самым координатам точек истока, как и дифференцирование (в предыдущем выражении для  интегрирование происходило по точкам истока, а дифференцирование, т.е. образование
интегрирование происходило по точкам истока, а дифференцирование, т.е. образование 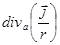 , производилось по точкам наблюдения).
, производилось по точкам наблюдения).
|
|
|
 .
.
Поскольку на поверхности проводников  , то
, то
 , что и требовалось доказать.
, что и требовалось доказать.
Дополнительный материал закончился.
Дифференциальные уравнения магнитного поля
1) 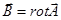 ,
,
 (дивергенция ротора всегда =0)
(дивергенция ротора всегда =0)
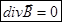 {уравнение (3) из лекции №13 }.
{уравнение (3) из лекции №13 }.
2) 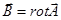 ,
,
 ,
,
 .
.
 {сравните с уравнением (1) лекции №13}.
{сравните с уравнением (1) лекции №13}.
3) Рассмотрим циркуляцию магнитного вектора  по произвольной замкнутой линии
по произвольной замкнутой линии  . На основании теоремы Стокса можно записать:
. На основании теоремы Стокса можно записать:
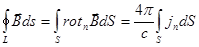 (напомним, что поверхностные интегралы могут быть распространены по любой поверхности
(напомним, что поверхностные интегралы могут быть распространены по любой поверхности  , опирающейся на контур
, опирающейся на контур  ).
).
Обратим теперь внимание на то, что  равно силе тока
равно силе тока  , проходящей через элемент поверхности
, проходящей через элемент поверхности  в направлении ее положительной нормали. Следовательно:
в направлении ее положительной нормали. Следовательно:

(алгебраическая сумма сил токов, пронизывающих контур  ; токи эти считаются положительными или отрицательными в зависимости от того, какую систему винта они создают с направлением обхода контура).
; токи эти считаются положительными или отрицательными в зависимости от того, какую систему винта они создают с направлением обхода контура).
 |
РИС.19-8
Очевидно, что циркуляция вектора напряженности магнитного поля по кривой, не охватывающей токов, равна помноженной на  сумме сил этих токов (взятых с надлежащими знаками).
сумме сил этих токов (взятых с надлежащими знаками).
Момент сил, действующих на виток с током в магнитном поле
 |
Сила, действующая на виток с током в постоянном (не зависящем от времени) магнитном поле, дается выражением
 (
( - контур витка).
- контур витка).
РИС.19-9
Если магнитное поле однородно, то вектор  можно вынести за знак интеграла. Поскольку
можно вынести за знак интеграла. Поскольку  , то сила, действующая на виток с током в однородном магнитном поле, равна нулю.
, то сила, действующая на виток с током в однородном магнитном поле, равна нулю.
Однако момент силы  , вообще говоря, в нуль не обращается.
, вообще говоря, в нуль не обращается.
 , где
, где  .
.
Вектор  - магнитный поток тока.
- магнитный поток тока.
 - векторная площадь витка (вектор единичной нормали направлен так, чтобы осуществлялась правовинтовая система).
- векторная площадь витка (вектор единичной нормали направлен так, чтобы осуществлялась правовинтовая система).
20 МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
Природа магнетизма
Притягиваются провода или отталкиваются – это зависит от направления тока. Но существуют ведь постоянные магниты. Мы знаем, что для возникновения электростатического поля нужны электрические заряды, а для возникновения магнитного поля нужны токи. Что за токи в постоянных магнитах?
Магнитный момент контура с током:
 |
 , где
, где  - вектор, направление которого совпадает с направлением внешней нормали, а величина равна численному значению площади контура, обтекаемого током.
- вектор, направление которого совпадает с направлением внешней нормали, а величина равна численному значению площади контура, обтекаемого током.
РИС.20-1
Электрон, движущийся в атоме по замкнутой орбите, создает ток, плотность которого
 , где
, где  - масса,,
- масса,, 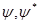 - волновые функции электрона,
- волновые функции электрона,  - плотность потока вероятности.
- плотность потока вероятности.
Если задано состояние электрона в атоме, т.е. заданы его волновые функции, то можно вычислить плотность замкнутого электронного тока в атоме и можно определить эффективную площадь орбиты электрона; следовательно, можно определить магнитный момент атома, обусловленный орбитальным движением электрона:
|
|
|
 , где
, где  =9.27×10-21 эрг/Гс=5.78×10-13 эВ/Гс - магнетон Бора,
=9.27×10-21 эрг/Гс=5.78×10-13 эВ/Гс - магнетон Бора,
 0,±1,±2…. – магнитное квантовое число.
0,±1,±2…. – магнитное квантовое число.
Магнитное квантовое число может принимать те или иные значения в зависимости от состояния, в котором находится атом, однако величина магнитного момента всегда будет целым кратным магнетона Бора.
Проекция механического момента на некоторое выделенное направление (ось  ):
):
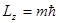 (где
(где  - то же самое магнитное квантовое число).
- то же самое магнитное квантовое число).
Отношение орбитального магнитного момента к механическому:
 - гиромагнитное отношение; это универсальная постоянная, которую можно измерить.
- гиромагнитное отношение; это универсальная постоянная, которую можно измерить.
Как будет показано в квантовой физике, если атом находится в основном состоянии (наинизшем по энергии) 1S, то магнитное квантовое число может иметь только одно значение 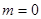 . Следовательно, магнитный момент атома в основном состоянии =0.
. Следовательно, магнитный момент атома в основном состоянии =0.
Опыт Штерна и Герлаха (1921 год)
(Определение магнитных моментов атомов и молекул)
Мы установили, что сила, действующая на магнитный диполь,  .
.
В однородном магнитном поле эта сила =0.
Чтобы определить величину магнитного момента, нужно пропустить пучок атомов через неоднородное магнитное поле и измерить отклонение. Очевидно, что магнитное поле должно быть неоднородным на расстояниях порядка размеров диполя (иначе будет только поворот в поле).

РИС.20-2
Для атомов в 1S-состоянии отклонение пучка на экране должно отсутствовать, так как  .
.
Оказалось, что имеет место отклонение, причем такое, которое соответствует магнитному моменту, равному  .
.
Собственный механический и магнитный момент электрона
Уленбек и Гаудсмит – спин. Это собственный момент количества движения электрона. Проекция собственного механического момента на произвольное выделенное направление (ось  ):
):  .
.
Получается гиромагнитное отношение другое:
 - спиновое гиромагнитное отношение вдвое больше орбитального!
- спиновое гиромагнитное отношение вдвое больше орбитального!
Значит, ели определить гиромагнитное отношение, то можно узнать, каково происхождение магнитного момента в веществе.
Опыт Эйнштейна – де Гааза (1915 г.)
 |
Существует жесткая связь между магнитным и механическим моментами. Значит, если мы тело намагнитим, т.е. ориентируем определенным образом магнитные моменты, то ориентируются определенным образом и механические моменты. Поскольку до намагничивания образец в целом момента количества движения не имел, то для выполнения закона сохранения момента количества движения образец должен закрутиться (как целое) в противоположном направлении. Это закручивание можно обнаружить и измерить.
РИС.20-3
Таким образом было установлено, например, что в ферромагнетиках их магнитные свойства обусловлены преимущественно спиновыми моментами (собственными).
Кроме магнитных моментов электронов – орбитальных и собственных (спиновых), вклад в магнитные свойства вещества дают также магнитные моменты ядер, которые, впрочем, много меньше электронных, так как масса ядер велика и скорости движения ядер малы.
Ядерный магнетизм обычно можно (удается) обнаружить лишь при температурах, близких к абсолютному нулю.
Ядерный магнетон Бора:  . Для протона масса
. Для протона масса  ; следовательно,
; следовательно,  .
.
Итак, магнитные свойства вещества определяются орбитальными и собственными магнитными моментами электронов.
К вопросу об эксперименте Эйнштейна – де Гааза
Магнитный момент одного атома  .
.
Момент количества движения одного атома относительно выделенной оси  ,
,
где  - гиромагнитное отношение.
- гиромагнитное отношение.
В результате намагничения тело в целом приобретет момент  . V -объем.
. V -объем.
Поскольку все эти силы внутренние, то, если тело находилось в покое, оно должно придти во вращение с угловой скоростью  , определяемой из уравнения
, определяемой из уравнения
 (вращение в обратную сторону).
(вращение в обратную сторону).
Отсюда можно найти  и определить природу магнетизма.
и определить природу магнетизма.
С точки зрения внешнего наблюдателя это соответствует протеканию в веществе токов намагничения.
В отсутствие внешнего магнитного поля – хаотическая ориентация элементарных магнитиков.
Включили поле – вещество намагничивается (упорядочиваются магнитики). Большинство веществ намагничиваются слабо. Сильно – только ферромагнетики. В подавляющем большинстве случаев снятие внешнего магнитного поля приводит к исчезновению намагниченности.
Токи намагничения
Микроскопическое магнитное поле возникает в результате движения элементарных частиц, это движение эквивалентно так называемым молекулярным токам.
Путем усреднения по физически малым объемам можно вычислить макроскопическое поле 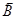 , которое возникает (формально) при протекании по веществу токов намагничения
, которое возникает (формально) при протекании по веществу токов намагничения 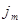 и
и  . Обычные токи назовем токами проводимости
. Обычные токи назовем токами проводимости  и
и 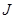 .
.
С учетом сказанного по теореме о циркуляции имеем:
 , что эквивалентно дифференциальному уравнению
, что эквивалентно дифференциальному уравнению
 .
.
Этот подход, вообще говоря, - формальный. Обычно используется более физический подход.
Введем вектор намагничивания  и определим его как сумму магнитных моментов частиц, содержащихся в единице объема:
и определим его как сумму магнитных моментов частиц, содержащихся в единице объема:  , где
, где  - концентрация частиц, имеющих магнитный момент
- концентрация частиц, имеющих магнитный момент  . Будем называть эти частицы молекулами.
. Будем называть эти частицы молекулами.
Теорема о циркуляции магнитного поля в веществе
 |
Мы определили вектор намагничивания
 .
.
РИС.20-4
Если намагничиваемое нами вещество (магнетик) – это просто цилиндр, объемом  , то полный магнитный момент этого цилиндра =
, то полный магнитный момент этого цилиндра =  :
:  .
.
С другой стороны, такой же точно полный магнитный момент создается током намагничения. Поскольку все токи внутри цилиндра компенсируются взаимно целиком и полностью, остается только ток на поверхности цилиндра:
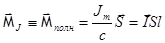 .
.
Поскольку вектор  , то
, то  .
.
На единицу длины (высоты) цилиндра приходится ток намагничения 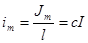 .
.
 .
.
Для намагничиваемого вещества в произвольном объеме справедливо соотношение:
 .
.
Полный ток намагничения:
 . Здесь
. Здесь  - произвольный замкнутый контур.
- произвольный замкнутый контур.
По теореме о циркуляции имеем:
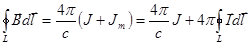 .
.
 .
.
Дифференциальная форма записи этого соотношения:
 .
.
Сравнивая с уравнением  , находим:
, находим: 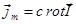 .
.
Если намагниченность однородна, т.е. 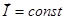 , то
, то  .
.
Если намагниченность неоднородна, т.е. зависит от координат - 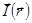 , то объемная плотность тока намагничения
, то объемная плотность тока намагничения  .
.
Введем вспомогательный вектор  .
.
Получаем:  , где
, где 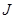 - это только ток проводимости.
- это только ток проводимости.
Дифференциальная форма:
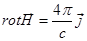 , где
, где  - плотность объемных токов проводимости.
- плотность объемных токов проводимости.
Смысл введения вектора  состоит только в том, чтобы убрать из соответствующих уравнений токи намагничивания и оставить только токи проводимости.
состоит только в том, чтобы убрать из соответствующих уравнений токи намагничивания и оставить только токи проводимости.
В учении о магнетизме вектор  играет такую же вспомогательную роль, что и вектор
играет такую же вспомогательную роль, что и вектор  в учении об электростатических полях.
в учении об электростатических полях.
Размерность векторов  и
и  одинакова, в вакууме они тождественно совпадают. Обычно
одинакова, в вакууме они тождественно совпадают. Обычно  измеряют в Гс (Гаусс), а
измеряют в Гс (Гаусс), а  в Э (Эрстед), хотя между этими величинами нет никакой разницы.
в Э (Эрстед), хотя между этими величинами нет никакой разницы.
Граничные условия для векторов  и
и 
Все магнитные среды делятся на 3 категории:
-парамагнетики – в них вектор намагничивания параллелен внешнему магнитному полю,  (O2, Al, Pt, FeCl3…);
(O2, Al, Pt, FeCl3…);
-диамагнетики – вектор  антипараллелен по отношению к внешнему магнитному полю (N2, CO2, H2O, Ag, Bi…);
антипараллелен по отношению к внешнему магнитному полю (N2, CO2, H2O, Ag, Bi…);
-ферромагнетики – сложная связь (нелинейная) между векторами  и
и  , имеется спонтанная намагниченность, гистерезис (Fe, Ni, Co, различные их сплавы).
, имеется спонтанная намагниченность, гистерезис (Fe, Ni, Co, различные их сплавы).
По историческим причинам пишут связь не между  и
и  , а между
, а между  и
и  в типичной форме:
в типичной форме: 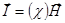 Þ {
Þ {  - тензор магнитной восприимчивости} Þ
- тензор магнитной восприимчивости} Þ
 .
.
В приближении изотропной среды  (
( - магнитная восприимчивость).
- магнитная восприимчивость).
 Þ
Þ  .
.
Магнитная проницаемость  .
.
В парамагнетиках  .
.
В диамагнетиках  .
.
 |
Рассмотрим границу раздела двух магнетиков и нормальную компоненту B.
РИС.20-5
Магнитных зарядов не существует, следовательно,  .
.
Отсюда 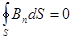 .
.  Þ
Þ 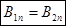 .
.
На границе раздела двух магнетиков нормальная компонента вектора  непрерывна.
непрерывна.
Рассмотрим тангенциальную компоненту B.

РИС.20-6
Теорему о циркуляции применяем к бесконечно малому прямоугольному контуру 
с длиной основания  , высота b пренебрежимо мала по сравнению с
, высота b пренебрежимо мала по сравнению с  (
( )
)
Пренебрегаем тогда вкладом в циркуляцию сторон  и
и  .
.
Циркуляция вектора  будет:
будет:
 .
.
По теореме о циркуляции эта же величина 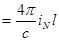 , где
, где 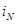 - слагающая поверхностного тока
- слагающая поверхностного тока  вдоль направления
вдоль направления  .
.
Приравнивая эти выражения, находим:
 .
.
Это же выражение можно записать в векторной форме.
Правая сторона:  .
.
Левая сторона: 
 .
.
Приравнивая, находим
|
|
|


