 |
Пример расчёта фильтра нижних частот
|
|
|
|
Фильтр нижних частот предназначен для выделения из входного напряжения ФЧВ среднего значения.
Частота минимальной гармоники в выходном сигнале ФЧВ будет равна 
, где 
– частота возбуждения датчика.
Например, 
, 
. Таким образом, ФНЧ должен ослабить напряжение с частотой в заданное число раз. Коэффициент подавления вычисляется исходя из точности схемы и условий быстродействия. Оставшиеся пульсации после фильтра должны быть меньше основной погрешности измерительного преобразователя. Например, если задана основная погрешность 
, то пульсации должны быть на уровне (5 
10) раз меньше, т.е. 
. Таким образом, коэффициент подавления фильтром наименьшей частоты должен быть равен 
.
Для упрощения выбираем схему фильтра, состоящую из пассивных R-C звеньев. Выберем трехзвенный фильтр. Его схема дана на рисунке 5.7.
Рис. 5.7. Пассивный трехзвенный фильтр нижних частот
Приближенно для трехзвенного фильтра коэффициент подавления можно оценить по следующей формуле: 
, откуда 
, 
или 
.
Выбираем значение емкости 
, значение сопротивления резистора будет равно 3,43 кОм.
Выбираем значение конденсатора [2]
.
Выбираем значение резисторов [1]
/
Для минимизации влияния входных токов ОУ выбираем резистор 
равным сумме резисторов 
:
.
Пример расчёта преобразователя напряжение-ток
Схема преобразователя напряжение-ток представлена на рисунке 5.8 [10]. Выходной ток данной схемы равен: 
.
Рис. 5.8. Схема преобразователя напряжение-ток
Допустим, что по заданию, диапазон изменения выходного тока 
и входное напряжение 
. Пусть, когда коэффициент 
, 
, когда 
, 
. Соответственно,
,
.
Из последнего выражения видно, что 
, а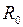 
находится из первого выражения: 
.
|
|
|
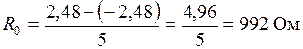Осталось сформировать напряжение 
. Для этой цели проще всего использовать схему параметрического стабилизатора напряжения, представленную на рисунке 5.9.
В качестве стабилитрона выберем прецизионный стабилитрон Д818Е [3] с номинальным напряжением стабилизации 9 В. Делитель напряжения 
должен обеспечить выходное напряжение 
. Рассчитаем делитель напряжения.
; 
.
Откуда 
. Задаваясь 
, находим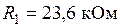 
. Выбираем [1]
,
.
Рис. 5.9. Формирователь напряжения смещения
Сопротивление 
– балластное должно пропустить ток стабилитрона и ток делителя 
.
.
Ток стабилитрона 
задаем 10 мА, тогда
.
Выбираем [1]
.
В качестве DA выбираем микросхему К140УД17А [5].
Пример расчёта генератора квадратурных напряжений
Схема генератора квадратурных напряжений представлена на рисунке 5.10.
Рис. 5.10. Квадратурный генератор синусоидальных колебаний
Передаточная функция петлевого усиления для этого генератора будет иметь вид: 
, а комплексный коэффициент передачи
.
Баланс фаз будет сохранен только на частоте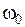 
, при которой мнимая часть знаменателя равна нулю.
, где 
; 
; 
; 
.
; 
.
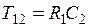Обозначая через 
коэффициент передачи звена на основе ОУ1, а через 
– коэффициент передачи звена на основе ОУ2 – интегратора, получим: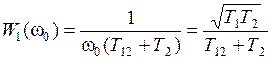 
,
.
Обозначим отношение 
к 
через 
. 
.
.
Тогда можно записать:
или 
.
Пусть, например, 
и, выбирая стабилитрон на 
, можно найти : 
.
Положим, что коэффициент передачи 
. Выберем 
, 
; 
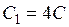. Тогда 
, 
, 
.
,
.
При этом 
, следовательно 
.
По заданию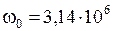 
, тогда 
.
Зададим значение емкости 
, тогда 
.
.
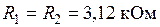Выбираем [1]
.
В качестве конденсатора выбираем слюдяной конденсатор КС0-1 [2]
,
.
Для расчета постоянной времени интегратора имеем 
, 
.
; 
, следовательно, 
.
.
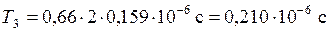Выбираем 
, тогда 
.
Выбираем [1, 2]:
,
.
В качестве стабилитрона выбираем стабилитрон КС133Г [3].
.
Используем два стабилитрона, поскольку необходимо двухполярное ограничение. Тогда резистор r рассчитываем из следующих соображений
|
|
|
.
Выбираем r [1]
.
Принципиальная схема генератора дана на рисунке 5.11.
Рис. 5.11. Принципиальная схема генератора квадратурных колебаний
|
|
|
