Производные и дифференциалы высших порядков

Дифференциал функции и его геометрический смысл

Теорема Ферма

Аn+ Вn = Сn*

где n- целое положительное число, большее двух, не имеет решения в целых положительных числах A, B, С.

Теорема Ролля

Если вещественная функция, непрерывная на отрезке и дифференцируемая на интервале, принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Пусть функция f(x):

-непрерывна на отрезке [a, b];

-дифференцируема в интервале (a, b);

-на концах отрезка [a, b] принимает равные значения.

Тогда существует точка c О (a, b) такая, что f'(c) = 0.Из теоремы Ролля следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна оси ОX

Доказательство. Если в промежутке, то во всех точках этого промежутка. Иначе наибольшее значение M функции превышает ее наименьшее значение m в промежутке. Поскольку на концах этого промежутка функция принимает одинаковые значения, то по крайней мере одно из значений, M или m, достигается во внутренней точке c промежутка. Тогда по теореме Ферма.

 

Физическая интерпретация теоремы Ролля. Пусть функция описывает смещение частицы из начального положения в зависимости от времени x ее движения по прямой. Тогда производная представляет собой мгновенную скорость движения частицы в момент времени c. Возвращение частицы в исходное положение возможно только при ее остановке в некоторый момент и перемещении в обратном направлении.

Теорема Лагранжа.

Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x0 (a < x0 < b), что

f(b) - f(a) = (b - a)f '(x).

Доказательство. Рассмотрим вспомогательную функцию F(x) = f(x) - k(x - a),где - угловой коэффициент хорды AB (смотри рисунок 2) 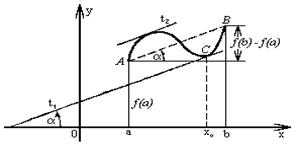.Эта функция удовлетворяет всем условиям теоремы Ролля.В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем

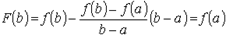
Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b). Следовательно, по теореме Ролля, в интервале (a, b) найдется такая точка x0, что F'(x0) = 0, т.е. f ' (x0) - k = 0 или

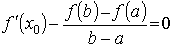
Отсюда имеем

f(b) - f(a) = (b - a)f ' (x0),что и требовалось доказать.

Теорема Коши об отношении приращения двух функций.

Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число c(a,b) такое, что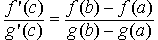

Доказательство

Заметим, что g(b) ≠ g(a). (Если g(b) = g(a), то, по теореме Ролля, существует число c(a,b) такое, что g ' (c) = 0.)

Введем обозначение:

Рассмотрим функцию 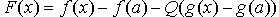, которая непрерывна на [a,b], дифференцируема на (a, b) и F(a) = F(b) = 0, т.е. функция F удовлетворяет условиям теоремы Ролля.

Следовательно, существует число c(a,b) такое, что F ' (c) = 0.

Так как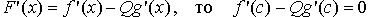

Правило Лопиталя

Производные и дифференциалы высших порядков

Пусть функция y = f (x) дифференцируема на некотором отрезке [ a, b ]. Значения производной f'(x) зависят от х, т.е. производная f'(x) тоже представляет собой некоторую функцию от х. Дифференцируя эту функцию, мы получаем производную от производной.

Опр. Производная от первой производной называется производной второго порядка или второй производной. Обозначается y''=(f'(x))'= f''(x).

Физический смысл второй производной: вторая производная f''(x) равна скорости изменения скорости, т.е. ускорению движущейся точки в момент времени х.

Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f'''(x).

Опр. Если определена (n -1) -я производная f (n -1) (x) и существует её произ­водная, то она называется n-й производной функции f(x): f (n) (x) = (f (n -1) (x))'.

Все производные, начиная со второй, называются производными высших порядков.

Функцию, имеющую на данном множестве конечную производную порядка n, называют n раз дифференцируемой на данном множестве.

Дифференциал функции y = f (x) выражается в виде dy = f'(x) dx. Тогда, если он является некоторой функцией от х, то справедливо следующее:

Опр. Дифференциал от дифференциала функции называется дифференциалом второго порядка или вторым дифференциалом: d (в квадрате)y = f''(x) dx 2.

Опр. Дифференциал от дифференциала n -го порядка называется дифференциалом (n +1)-го порядка.

Поделиться:

Воспользуйтесь поиском по сайту: