Порядок расчета индуктивного преобразователя с П-образным и Ш-образным сердечником и плоским якорем

Расчет преобразователя с П-образным сердечником (рисунок 4, а) является частным случаем расчета преобразователя с Ш-образным сердечником (рисунок 5, а), поэтому будем рассматривать только последний.

Магнитная цепь (рисунок 5, б) обычно выполняется симметричной от­носительно среднего сердечника, на котором расположена катушка (изображена жирными линиями). Поэтому достаточно рассчитать одну её половину, уменьшив сечение среднего сердечника вдвое и сохранять ту же величину намагничивающей силы катушки.

Изложение принципов расчета данного индуктивного преобразо­вателя будет проводить совместно с решением конкретного примера.

Исходные данные примера:

- из заданных габаритов имеем (рисунок 5, а) a = f = t = b = 5мм = 5x10^-3м; c= 16мм = 16x10^-3м; h = 30мм = 30x10^-3м;

- предел измерения Δd = 0,2 мм = 0,2 x10^-3м;

- измерительное усилие не более 3 Н;

- передаточное отношение 500 ÷ 800 см/мм;

- частота питающего напряжения 50 Гц.

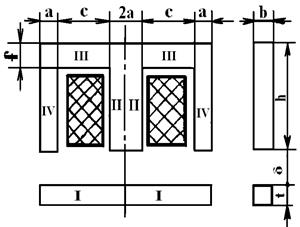
Рисунок 5 – Индуктивный преобразователь с Ш-образным сердечником

 

1. Согласно выражения (3) определяем количество витков катушки, предварительно задавшись:

d_t = 0,2 мм=0,2 x10^-3м; провод марки ПЭВ-2;

f₀ = 0,55 (таблица 1); толщина стенок каркаса катушки 1,5 мм.

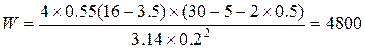витков.

2. Согласно выражения (4) определяем начальный зазор, мм:

,

.

3. Задаемся величиной индукции в среднем сердечнике согласно (6) – B_II=0,2 Тл.

При расчете магнитной цепи удобно использовать схемы заме­щения. Схема замещения (рисунок 6) составляется сообразно конфи­гурации магнитопровода. Все участки магнитных сопротивлений цепи на схеме обозначены сосредоточенными магнитными сопротивле­ниями, а ЭДС катушки К показана как источник потока.

Так как рассматриваемая цепь симметрична, мы условно примем, что магнитное сопротивление среднего сердечника состоит из двух равных параллельно включенных сопротивления сердечника Z_MII и двух равных сопротивлений воздушных зазоров R_dII.

Рисунок 6 – Схема замещения

 

Для любой половины магнитопровода полное магнитное сопротивление цепи будет равно сумме сопротивлений остальных участков цепи Z_Mi и сумме сопротивлений двух воздушных за­зоров R_di:

. (8)

Суммарное магнитное сопротивление ввей цепи будет равно:

. (9)

Общий магнитный поток F_S, создаваемый катушкой преобразователя будет равен

F_S = F₁ + F₂ = 2F₁, (10)

где F_{1(2 )} – магнитный поток правой или левой половины магнитопровода, Вб.

4. Определение магнитного сопротивления воздушных зазоров.

При расчетах обычно пользуются магнитной проводимостью воздушных зазоров, величиной обратной сопротивлению

Точность расчета преобразователя в основном определяется точностью определения проводимости воздушных зазоров.

Магнитное поле в зазоре не является плоскопараллельным, магнитный поток выпучивается из-под полюсов. Поэтому для расчета проводимости воздушного зазора применяют метод разбивки (метод Ротерса) магнитного поля на простые геометрические фигуры, проводимость которых затем и определяется по известным формулам, приведенным в таблице 3.

В нашем случае поле разбивается на восемь простых фигур (рисунок 5, б).

Координаты поля выпучивания X¢, X¢¢, Z¢_a, Z¢¢_a, Z¢_b, Z¢¢_b определяется по графику на рисунке 7 и ниже приведенным рекомендациям.

Рисунок 7 – Координаты поля выпучивания

Координата X¢ обычно принимается равной

.

Из рисунка 7 по известной величине определяем . Расчет удобно начинать с максимальной величины воздушного зазора при которой ток проходящий через катушку преобразователя имеет наибольшее значение. И если при этих условиях определить параметры катушки, то плотность тока, в процессе работы преобразователя, не превысит расчетной величины.

;

; .

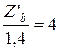С достаточной для практики точностью рекомендуется принимать

.

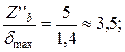
По известной величине и по графику на рисунке 7 определяем .

, м.

Далее определяется по формулам таблицы 3 проводимости отдельных фигур.

5. Проводимость половины полого цилиндра G (фигура 2, рисунок 5, б). Таких фигур в зазоре d_II две штуки, а в зазоре d_IV три штуки.

где m₁ – средняя толщина стенки цилиндра равная

.

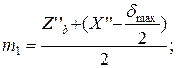
Таблица 3 – Основные фигуры аналитическое выражение их магнитных проводимостей.

Эскиз фигуры	Формула магнитной проводимости
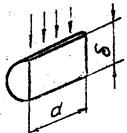Полуцилиндр
Четверть цилиндра

 

Продолжение таблицы 3

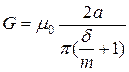
Половина полого цилиндра
Четверть полого цилиндра
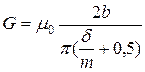
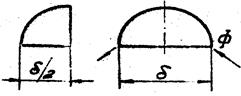Сферический квадрант
Половина сферического квадранта
Квадрант сферической оболочки
Половина квадранта сферической оболочки

 

 

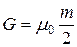
Продолжение таблицы 3

Тело вращения (полуцилиндр)
Тело вращения (полукольцо)

6. Проводимость половины цилиндра (фигура 2). Для зазора d_IV имеется три таких фигуры, а для d_II две. Тогда:

.

7. Проводимость квадранта полого шара (фигура 3). Только у зазора d_IV, имеется две таких фигуры. Тогда:

.

8. Проводимость шарового квадранта (фигура 4). Две таких фигуры только у зазора d_IV, значит:

.

9. Проводимость зазора под полюсами (фигура 5) по одной фигуре у каждого полюса

.

10.Проводимость четверть цилиндра (фигура 6). По одной фигуре у каждого зазора:

.

11. Проводимость четверть полого цилиндра (фигура 7). По одной фигуре у каждого зазора:

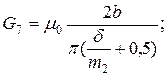
где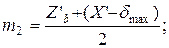

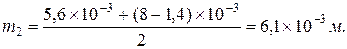
12. Проводимость G₈ квадрантов сложной формы заключенных между фигурами 6,7 и 1,2 рекомендуется принимать

.

Общая магнитная проводимость воздушных зазоров определится как сумма их составляющих.

Для зазора :

= + +

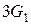, (11)

 

где Гн/м.

После подстановки получаем:

 

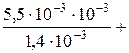
Гн.

Сопротивление: 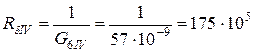1/Гн.

Для зазора :

, (12)

После подстановки получаем:

Гн.

Сопротивление этого зазора:

1/Гн.

13. Определение магнитного сопротивления стальных участков цепи.

Комплексное сопротивление стального сердечника определяется по формуле:

,

где – удельное реактивное и активное магнитное сопротивление, м/Гн; определяется по экспериментальным графикам (рисунок 8) в зависимости от величины магнитной индукции В_i;

l_i, S_i – средняя длина и поперечное сечение i-того сердечника.

Для нашего случая магнитная индукция в среднем сердечнике B =0,2 Тл, а его магнитный поток составляет: 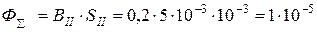Вб.

Следовательно: Вб.

По потоку Ф₁ определяют величины индукции в каждом звене магнитопровода.

Так как поперечное сечение звеньев I, III, IV равны (5х5), то и величины индукции этих звеньев будут также равны:

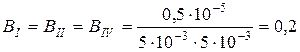Тл.

Для этого значения индукции по графикам 8 (рисунок 8, б) для стали Э-12 определяем:

м/Гн, м/Гн,

=(14,4+j3,3) 1/Гн.

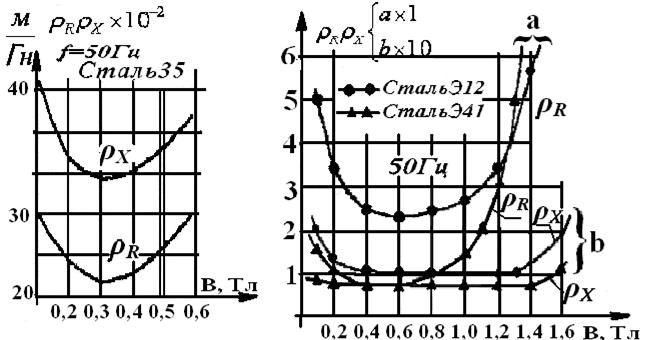
Рисунок 8 – Экспериментальные графики для определения

Суммарное магнитное сопротивление одной половины магнитной цепи преобразователя:

= 1/Гн. (13)

Суммарное магнитное сопротивление всей цепи составит:

1/Гн. (14)

Модуль этого сопротивления:

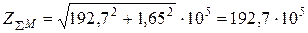1/Гн.

Полное комплексное электрическое сопротивление катушки преобразователя определяется из следующей формулы:

, (15)

где – активное сопротивление преобразователя из-за потерь в стали на

гистерезис и вихревые токи, Ом;

– реактивное индуктивное сопротивление катушки, Ом, 1/Гн;

– круговая частота, где f₀ – частота в герцах. Для нашего случая ;

R_a – активное сопротивление катушки преобразователя, равное

, (16)

где ρ – удельное сопротивление для медной проволоки (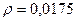 Ом×мм²/м);

l_ср – средняя длина витка (м) (рисунок 9);

Рисунок 9 – Вид преобразователя с Ш-образным сердечником

q – поперечное сечение полого провода (таблица 2).

Ом.

Откуда модуль сопротивления по формуле (15):

.

 

Эффективное значение тока, протекающего через катушку преобразователя для создания выбранного магнитного потока будет равно

А.

Плотность тока в обмотке:

А/мм², А/мм².

Напряжение питания катушки будет равно

В.

Для приближённого определения передаточного отношения преобразователя и определения измерительного усилия необходимо определить полное сопротивление магнитной цепи и полное сопротивление катушки при наименьшем зазоре :

мм.

При выполнении повторного расчёта при зазоре сопротивления остальных участков будем считать неизменными. Для этих условий м; м; м; м.

Согласно формул (11) и (12) получим:

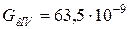Гн;

1/Гн;

Гн;

1/Гн.

Суммарное магнитное сопротивление одной половины цепи согласно (13) равно

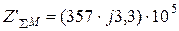1/Гн,

а сопротивление всей цепи согласно (14) равно

1/Гн.

Модуль этого сопротивления:

1/Гн.

Наконец, согласно с формулой (15) получим модуль полного электрического сопротивления катушки: Ом.

Таким образом, при изменении зазора между якорем и неподвижным сердечником на величину 0,2 мм сопротивление катушки изменилось на 160 Ом. Считая, что передаточное отношение К_ип на всём пределе измерения постоянно, определим его значение:

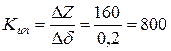Ом/мм.

Для построения характеристики преобразователя определяются для нескольких значений (в пределах рабочего хода якоря) величины сопротивлений преобразователя.

Измерительное усилие F_из преобразователя определяется, исходя из величины максимальной электромеханической силы притяжения F_э якоря к сердечнику, которая определяется по приближённой формуле, полученной из формулы Максвелла. Для недифференциального преобразователя сила притяжения одного полюса равна:

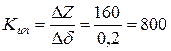Ом/мм. Ошибка! Ошибка связи. (17)

Эта формула справедлива для определения величины электромагнитной силы действующей между двумя параллельными плоскостями, находящимися на небольшом расстоянии (1-2мм).

У дифференциального преобразователя на якорь действует разность сил, направленная в сторону меньшего зазора и равная

. (18)

Для нашего примера (дифференциальный преобразователь) на одну пару полюсов разность составит:

Н.

Для 4-х полюсов: Н.

Измерительное усилие F_из преобразователя должно быть больше электромеханической силы в 5-10 раз. Примем его равным 3Н.

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: