Связь с гибким автоматизированным производством.

Автоматизирование проектирование изделий радиоэлектроники заканчивается изготовлением конструкторской документации и управляемых программа на машинных носителях для автоматизированного технологического оборудования. Аттестованные машинные носители с управляемыми программами в дальнейшем копируются и обеспечивают эффективную перестройку исполнительного оборудования с одного изделия на другое, что является одним из условий реализации гибкого автоматизированного производства (ГАП)

Одновременно возникает обратная информационная связь ГАП с САПР через измерительно-вычислительный комплекс, в качестве которого используются автоматизированные тестеры контроля и измерения РЭУиА, технологии их изготовления. Информационно-вычислительный комплекс наполняет базу данных САПР достоверными проектными норами и параметрами технологии материалов и элементов. Технологические ограничения и разбросы описывающие условия конкретного ГАП так попадают в САПР в качестве исходных данных. Используя эти данные статистически достоверные автоматизированного проектирования служат основой получения высокого выхода годных изделий в производстве.

Вопрос №7

Конструкторское проектирование РЭУиА и топологическое проектирования БИС.

Конструкторское проектирование – один из важнейших этапов проектирования. При проектировании БИС этот этап носит название топологического проектирования.

Исходными данными для конструкторского и топологического проектирования являются данные функционального и схемотехнического проектирования. Результатом конструкторского и топологического проектирования является конструкторская документация и машинные носители для технологического программно управляемого оборудования. Это могут быть станки с ЧПУ, фотонаборные установки. Для конструкторского проектирования в целом характерно восходящее проектирование, т.е. на базе определенной серии микросхем, строительные блоки и типовые элементы замены (ТЭЗы), разрабатываются панели, рамки и стойки. На каждом шаге проектирования последовательно решаются задачи компоновки элементов конструкции в узлы, размещение этих узлов на конкретным установленным местам и трассировка соединений между элементами. Эта группа задач относится к коммутированно-монтажному проектированию.

Самостоятельной группой задач являются задачи изготовления или выпуска конструкторской документации и машинных носителей информации для управления технологическим оборудованием.

Вопрос №8

Математическое моделирование конструкторского проектирования.

Основными задачами коммутированно-монтажного топологического проектирования для БИС являются следующие задачи:

1) Компоновка конструктивов i в конструктивы i -1 уровня (компановка микросхем в ячейке, ячеек в блоки, элементов И, ИЛИ, НЕ в корпусах микросхем и т.д.)

2) Размещение конструктивов i уровня в конструктивы i -1 уровня (размещение микросхем на плате, ячеек в блоки и т.д.)

3) Трассировка монтажных соединений между конструктивами на всех уровнях (соединения микросхем на плате, монтажные и межблочные соединения)

Каждая из перечисленных задач реализуется отдельным пакетом программ и может решаться отдельной подсистемой САПР.

Если компановка неавтоматизарована, то информация задается принципиальной схемой, и проектируется на ЭВМ начиная с размещения.

Если размещение неавтоматизировано, то информация задается описанием координат соединительной схемой и на ЭВМ выполняется трассировка и выпуск документации.

Если же все проектирование неавтоматизировано и сделан эскиз топологическими схемами исходной информации служит чертеж, который кодируется на кодировщике и вводится на ЭВМ, где выполняется построение и совмещение чертежей, а также формирование и выпуск конструкторской документации, технологической документации для управления техническими автоматами.

Контроль полученных конструкторских решений включает контроль соответствия конструкторским исходным принципиальным схемам и контроль выполнения заданных конструкторских технологических ограничений. В случае БИС контролируется выполнение метрических норм на размеры областей, на расстояние между областями в одном слое, на перекрытие областей различных слоев. В соответствии топологические принципиальные схемы проверяются путем восстановления принципиальной схемы по топологии, заданной набором файлов, послоечных чертежей.

Вопрос №9

Алгоритмы компановки.

Процесс перехода от электрической схемы к конструктивному распределению или разбиению всех элементов на группы соответствующие конструктивному различению уровней, называется компановкой, которая может выполняться снизу вверх и, наоборот. В первом случае осуществляется последовательно компановка конструктивы низших уровней в конструктивы высших уровней. Во втором случае конструктивы высших уровней последовательно разбиваются на конструктивы меньшей сложности, пока не будет получена схема связей конструктивов этого уровня. В зависимости от этого выделяют 3 постановки задач компановки.

1. Типизация – разбиение схемы на конструктивные элементы или топологические компоненты БИС различных типов и определяют тип их номенклатуры.

2. Покрытие – преобразование исходной схемы в схему соединений модулей, номенклатура которых задана. Это покрытие функциональной схемы из элементов И, ИЛИ, НЕ, набора микросхем 155 серии.

3. Разрезание – разбиение исходной схемы на части, типы которых либо заданы, либо должны быть определены в процессе решения с минимализацией числа связей между ними.

Оптимальный вариант результата компановки выбирается из условий инимализации числа модулей и числа связей между ними.

Кроме критериев числа типов модулей межмодульных связей используют следующие: общее число модулей, число используемых элементов во всех модулях скомпанованной схему, суммарная площадь занимаемая элементами и соединениями, параметры тепломассы обмена между элементами в блоке и совместимость элементов в модуле.

Вопрос №10

Исходные алгоритмы компановки условно разбивают на 5 групп:

1. Алгоритмы, использующие методы целочисленного программирования.

2. Последовательные алгоритмы.

3. Итарационные алгоритмы.

4. Смешанные алгоритмы.

5. Алгоритмы, основанные на методе ветвей и границ.

Алгоритмы 1 группы могут обеспечивать такое решение, но из-за их сложности и больших затрат машинного времени они не нашли практического применения.

Более распространенными являются остальные алгоритмы до 5-й группы, которые хотя и являются приближенными, но приводят к удовлетворительным результатам и позволяют честь основные критерии компановки.

Как правило в алгоритмах компановки математической моделью объекта является граф, вершины которого соответствуют модулю, а ребра межмодульным соединением. В последних алгоритмах сначала выбирается первая вершина графа и последующие соединения к ней других вершин из числа нераспределенных формируется первый кусок графа, затем выбирается второй и т.д. до полного размещения.

Итерационный алгоритм применяется для улучшения либо результатов в компановки, полученных последовательными алгоритмами, либо начала произвольного разрезания графа на куски путем парной или групповой перестановки вершин графа из различных кусков с проверкой улучшения заданных критериев при перестановке.

Задача компановки чаще всего решается смешанными алгоритмами в два этапа: начальная компановка – последовательными алгоритмами, а улучшение результатов начала компановки – итерационными для удовлетворению принятых критериев.

Вопрос №11

Исходными данными для задачи покрытия является функциональная схема и логические схемы типовых конструктивных илементов, предназначенных для конструкторской реализации этой схемы. Необходимо каждый логический элемент функциональной схемы реализовать логическими элементами, входящими в состав типовых модулей с учетом огрничений и определенных требований.

Наборы типовых модулей включают в себя:

1) элементные модули, состоящие из логически несвязанных элементов многоцелевого назначения;

2) функциональные модули, состоящие из логических элементов, связанных между собой и реализующих определенную функцию.

Задачи покрытия схемой элементными модулями может быть сведена к задаче целочисленного программирования и для однотипных модулей, представляющих собой задачу разбиения, разрезания. Задача покрытия схему функциональными модулями более сложная, т.к. надо распознавать различные структуры модулей в общей функциональной схеме.

Математическая формулировка задачи покрытия – пусть задан набор модулей T = (t₁, t₂,…t_n), где n – число типов модулей в наборе. Этот набор характеризуется матрицей А, равной [ aij ]m´n, в которой aij – соответствует числу логических элементов i типа в модуле j типа, а m - общее число типов логических элементов во всех модулях, заданного набора.

Поэлементый состав заданной функциональной схемы характеризуется: , где b_i – число элементов i- типа в схеме.

Введем целочисленную переменную X_j, характеризующее количество модулей, необходимых для покрытия схемы.

В простом случае задачу отыскания покрытия с минимальным количеством модулей.

Тогда целевая функция примет вид: 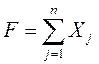, где X_j – целое число.

Для минимизации стоимости покрытия используют целевую функцию вида: , C_j – стоимость модулей j типа.

Простой эвристический алгоритм представляет все модули элементами. Более сложные алгоритмы работают в несколько этапов. Сначала выделяют подсхемы, т.е. группы максимально связанных между собой элементов, соответствующим размерам модулей, осуществляют переборы этих подсхем и их сравнение с модулями набора. Подсхему закрепляют за тем модулем, который вмещает максимальную ее часть. Процесс продолжается до тех пор, пока в схеме не останется незакрепленных элементов. Затем для улучшения полученного результата осуществляются парные перестановки однотипных элементов различных модулей для уменьшения межмодульных связей.

Обычно логическую схему представляют ориентированным графом, множество вершин которого соответствует элементам схемы, а множество рёбер связям между элементами. Аналогично каждому модулю поставим в соответствие ориентированный подграф и в результате получим некоторое множество m ориентированных подграфов, соответствующим модулем заданного набора. Задача покрытия формулируется как покрытие графа G= (A,X) подграфами из множества M=(G`1,G`2…G`n).

Наибольшие трудности при решении задачи в такой постановки возникают при отождествлении элементов схемы с элементами набора модулей в зависимости от критериев оптимизации вершинам графов G и G` присваиваются определённые веса и задачу покрытия решают в несколько этапов. Сначала вершины графа G рассматриваются как материальные точки единичной массы. Если вершины смежные то для них вводятся силы притяжения и кроме того между любыми вершинами графа вводятся силы отталкивания. Проводят размещения вершин графа на плоскости так, чтобы обеспечить равновесие всех элементов при этом наиболее связанные вершины должны быть поблизости друг от друга. Далее применяются критерии геометрической близости, производят разбиение множества элементов на непересекающиеся множества, из которых образуются модули определенного типа, т.к. этот процесс может привести к увеличению связи между модулями, то после объединения элементов в модули по результатам размещения осуществляют парные перестановки однотипных элементов различных модулей.

Вопрос №12

Задачи разбиения.

Эта задача заключается в том, чтобы разрезать исходную схему на части так, чтобы образовались конструктивные узлы более низкого уровня иерархии с учетом определенных требований и ограничений. К наиболее важным критериям относится длина внешних связей, характеризующаяся либо числом межузловых соединений, либо число внешних выводов всех узлов.

Объем конструкции характеризуется числом узлов разбиения, числом различных типов узлов и неразрывностью функционального назначения узлов.

Для формализации задачи разбиения представим исходную схему графом, в котором элементы – вершины графа, а соединения между ними – ребра.

Вопрос №13

Для решения задачи разбиения используется приближённые алгоритмы, которые можно разбить на две группы:

1) Последовательный

2) Итарационный

Последовательные алгоритмы. Задачи разбиения.

Общая задача для всех последовательных алгоритмов разбиения – это последовательное заполнение узлов элементами и проверка заданных ограничений. На каждом шаге выбирается элемент с максимальным или минимальным значением некоторого показателя, характерезующего целесообразность выбора данного элемента. Наиболее распространенным алгоритмом разбиения последнего типа является метод максимума коньюкции и минимума дизъюнкции.

Итерационный алгоритм – эти алгоритмы в зависимости от исходного варианта могут быть двух типов. Исходным вариантом для итерационных алгоритмов 1-го типа является некоторый начальный вариант разбиения, полученный вручную или с помощью одного из последовательных алгоритмов. Основу этих алгоритмов составляет итерационный процесс обмена местами элементов – это парные или групповые перестановки. Замена элементов производится с целью уменьшения или увеличения выбранного критерия оптимизации.

Парные перестановки улучшают первоначальное разбиение, но не обеспечивают достижение оптимального разбиения по 2-м причинам:

1) Из-за ограничения числа элементов участвующих в обмене

2) Из-за наличия в узлах сильно связанных элементов

Поэтому для улучшения разбиения иногда применяют групповые перестановки. Этот метод не целесообразно применять для задач в которых функция F имеет большое число локальных экстремумов. Исходным вариантом для итерации алгоритма 2-го типа является разбиение схемы на две части: Сначала осуществляют парные перестановки элементов из этих частей для минимизации связей между ними, затем рассматривается поочерёдно каждая из частей и в свою очередь разбивается на 2 блока с последовательной минимизацией связей между блоками путём перестановок элементов. Этот процесс продолжается до тех пор пока не будут получены все узлы разбиения.

Вопрос №15

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: