Указания по выполнению контрольных работ

ВЫСШАЯ МАТЕМАТИКА

 

Программа и контрольные задания

Для студентов инженерно-экономических специальностей
заочной и вечерней форм обучения

 

Ускоренный курс

 

 

СЕМЕСТР 2

 

 

Красноярск 2005

 

Указания по выполнению контрольных работ

Студент должен выполнять один тот же вариант всех контрольных работ. Чтобы определить свой вариант, нужно разделить на 25 число, полученное отсечением двух цифр от номера студенческого билета (шифра), обозначающих год поступления в университет. Остаток от деления и есть номер вашего варианта. Если остаток равен нулю, то номер вашего варианта равен 25. Например, если шифр студента равен 23602, тогда остаток от деления 236 на 25 будет равен 11 и, следовательно, решать нужно вариант №11; если шифр студента равен 57501, тогда остаток от деления 575 на 25 будет равен 0 и, следовательно, решать нужно вариант №25.

При выполнении контрольных работ необходимо соблюдать следующие правила:

1. В начале работы разборчиво написать свою фамилию, инициалы, шифр, номер и вариант контрольной работы и дату отсылки ее в университет.

2. Каждую контрольную работу выполнять в отдельной тетради (или на белой бумаге формата А 4), авторучкой или распечатанной на принтере с полями не менее 3 см для замечаний рецензента.

3. Решения задач располагать в порядке номеров, указанных в контрольных работах. В начале каждого решения записывать условие задачи (без сокращений).

4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов. Обязательно, если требуется, выполнять чертежи с пояснениями и нарисованными аккуратно.

Контрольные работы, выполненные с нарушением изложенных правил или не своего варианта, не засчитываются и возвращаются без проверки.

Получив прорецензированную работу, студент обязан исправить в ней отмеченные ошибки и недочеты. Если работа не зачтена, ее необходимо в короткий срок либо выполнить заново (целиком), либо решить заново задачи, указанные рецензентом. Исправленную работу следует посылать в университет вместе с незачтенной. Зачтенные контрольные работы предъявляются преподавателю при защите перед зачетом или экзаменом.

 

Программа курса «Высшая математика»
Второй семестр

 

РАЗДЕЛ 1. Интегральное исчисление

1.1. Первообразная. Неопределенный интеграл и его свойства.

1.2. Табличные интегралы. Замена переменной и интегрирование по частям в неопределенном интеграле.

1.3. Многочлены. Теорема Безу. Основная теорема алгебры. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители.

1.4. Разложение рациональных дробей на простейшие.

1.5. Интегрирование рациональных дробей.

1.6. Интегрирование тригонометрических выражений.

1.7. Интегрирование некоторых иррациональных и трансцендентных функций.

1.8. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл, его свойства.

1.9. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов.

1.10. Геометрические и механические приложения определенного интеграла.

1.11. Несобственные интегралы с бесконечными пределами и от неограниченных функций, их основные свойства. Признаки сходимости несобственных интегралов.

1.12. Двойной интеграл. Вычисление двойного интеграла. Двойной интеграл в полярных координатах. Вычисление площадей и объемов с помощью двойных интегралов.

РАЗДЕЛ 2. Дифференциальные уравнения

2.1. Дифференциальные уравнения первого порядка. Частное и общее решение (интеграл) дифференциального уравнения. Теорема Коши. Геометрический смысл дифференциального уравнения первого порядка.

2.2. Дифференциальные уравнения с разделяющимися переменными.

2.3. Однородные дифференциальные уравнения первого порядка. Дифференциальные уравнения первого порядка, сводящиеся к однородным.

2.4. Линейные дифференциальные уравнения первого порядка. Метод подстановки (метод Бернулли). Метод вариации постоянной (метод Лагранжа).

2.5. Дифференциальные уравнения первого порядка, сводящиеся к линейным. Уравнение Бернулли.

2.6. Дифференциальные уравнения 1-го порядка, сводящиеся к уравнениям в полных дифференциалах. Интегрирующий множитель.

2.7. Какое решение ДУ-I называется особым? Как оно может быть связано с общим решением. Огибающая семейства интегральных кривых. Почему огибающая семейства интегральных кривых ДУ-I всегда является решением, притом особым? Может ли дифференциальное уравнение y' = f (x,y) иметь решения, которые не являются ни частными, ни особыми?

2.8. Дифференциальные уравнения высших порядков. Основные понятия. Особенности решений дифференциальных уравнений высших порядков по-сравнению с первым. Задача Коши и краевая задача.

2.9. Уравнения, допускающие понижение порядка. Уравнения вида . Уравнения вида .

2.10. Однородные линейные дифференциальные уравнения. Свойства решений таких уравнений. Определитель Вронского. Фундаментальная система решений.

2.11. Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение.

2.12. Неоднородные линейные дифференциальные уравнения. Свойства решений таких уравнений. Структура общего решения неоднородных уравнений.

2.13. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов.

2.14. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами. Метод вариации постоянных (метод Лагранжа).

РАЗДЕЛ 3. Ряды

3.1 Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.

3.2 Ряды с неотрицательными членами. Признаки сходимости.

3.3 Знакопеременные ряды. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютно сходящихся рядов.

3.4 Функциональные ряды. Область сходимости. Равномерная сходимость. Признак Вейерштрасса.

3.5 Свойства равномерно сходящихся рядов: непрерывность суммы ряда, почленное дифференцирование и интегрирование.

3.6 Степенные ряды. Теорема Абеля. Круг сходимости. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. Приложение рядов.

3.7 Ряды Фурье. Периодические величины и гармонический анализ. Ортогональность системы тригонометрических функций. Сходимость ряда Фурье. Ряды Фурье для четных и нечетных функций. Ряд Фурье с произвольным периодом.

РАЗДЕЛ 4. Теория вероятностей

4.1. Предмет теории вероятностей. Сущность и условия применимости теории вероятностей. Основные понятия теории вероятностей. Случайное событие. Классификация событий. Алгебра событий.

4.2. Классическое определение вероятности. Комбинаторика. Комбинаторные способы вычисления вероятности.

4.3. Статистическое определение вероятности. Частота и вероятность. Геометрическое определение вероятности. Понятие об аксиоматическом построении теории вероятностей. Вероятностное пространство.

4.4. Основные формулы вычисления вероятностей. Условная вероятность. Независимые и зависимые события. Вероятность произведения и суммы событий. Формула полной вероятности. Формула Байеса.

4.5. Повторные независимые испытания; формула Бернулли. Теоремы Пуассона и Муавра-Лапласа.

4.6 Случайные величины. Функция распределения и ее свойства. Закон распределения дискретной случайной величины. Ряд распределения. Плотность распределения непрерывной случайной величины и ее свойства.

4.7. Основные числовые характеристики случайной величины: математическое ожидание, дисперсия и среднее квадратическое отклонение. Моменты случайной величины.

4.8. Основные законы распределения дискретных случайных величин (биномиальное, Пуассона, геометрическое распределения). Основные законы распределения непрерывных случайных величин (равномерное, экспоненциальное и другие). Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях.

4.9. Нормальное распределение и его свойства. Особая роль нормального распределения: центральная предельная теорема. Распределения, связанные с нормальным: Пирсона, Стьюдента, Фишера.

4.10. Закон больших чисел и его следствия. Неравенство и теорема Чебышева.

4.11. Закон распределения вероятностей для функций от известных случайных величин.

4.12. Системы случайных величин. Матрица и функция распределения системы двух случайных величин. Условный закон распределения. Регрессия. Корреляционный момент и коэффициент корреляции.

4.13. Случайные процессы. Цепи Маркова и их использование в моделировании социально-экономических процессов.

РАЗДЕЛ 5. Математическая статистика

5.1. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения, выборочная средняя и дисперсия.

5.2. Статистическая оценка параметров. Требования к статистическим оценкам: состоятельность, несмещенность, эффективность. Методы моментов и максимального правдоподобия.

5.3. Интервальное оценивание. Метод доверительных интервалов.

5.4. Статистическая проверка гипотез. Статистические критерии. Проверка гипотезы о значении параметров нормального распределения. Проверка гипотез о равенстве долей и средних.

5.5. Проверка гипотезы о виде распределения. Критерии Пирсона и Колмогорова.

5.6. Понятие о корреляции и регрессии. Метод наименьших квадратов. Статистические методы обработки экспериментальных данных.

ЛИТЕРАТУРА

1. Высшая математика для экономистов. Учебник для вузов /Под ред. Н.Ш. Кремера.–М: ЮНИТИ–М.,1998.

2. Гусак А.А. Высшая математика. В 2-х т.: Учеб. пособие. Мн: ТетраСистемс, 1998.

3. Шипачев В.С. Высшая математика. М: Высш. шк., 2003.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражениях и задачах. Ч.1,2. М: Высш. шк., 2003.

5. Письменный Д.Т. Конспект лекций по высшей математике. В 2-х т. М: Айрис-пресс, 2002.

6. Натансон И.П. Краткий курс высшей математики. СПб.: Лань, 2001.

7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры: Учеб. для вузов.-М.: Высш.школа,1998.

8. Ильин В.А., Позняк Э.Г. Математический анализ. М.:ФИЗМАТЛИТ. 2001.

9. Красс М.С., Чупринов Б.П. Основы математики и ее приложения в экономическом образовании. М.: Дело, 2001.

10. Красс М.С. Математика для экономических специальностей. М.:ЮНИТИ–М, 1999.

11. Общий курс высшей математики. Учебник /Под ред. В.И. Ермакова.–М: ИНФРА–М,1999.

12. Солодовников А.С., Байбацев В.А. Математика в экономике. В 2-х ч. М.: Финансы и статистика,2000.

13. Кремер Н.Ш. Теория вероятностей и математическая статистика: М: ЮНИТИ, 2003.

14. Гмурман В.Е. Теория вероятностей и математическая статистика. М: Высш. шк., 2000.

15. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М: Высш. шк., 2000.

16. Калинина В.Н., Панкин В.П. Математическая статистика. М: Высш. шк., 1998.

17. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. М: ИНФРА-М, 1997.

КОНТРОЛЬНАЯ РАБОТА №2

СЕМЕСТР 2

Вариант 1

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	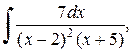е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. Брошены две игральные кости. Найти вероятность того, что выпадет хотя бы одно четное число.

4. Два охотника стреляют одновременно и независимо друг от друга по зайцу. Заяц будет подстрелен, если в него попадет хотя бы один из охотников. Найти вероятность того, что заяц будет подстрелен, если вероятность попадания для первого охотника равна 0,8, а для второго – 0,75.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Произведено 8 независимых испытаний, в каждом из которых вероятность появления события A равна 0,1. Найти вероятность того, что событие A появится хотя бы 2 раза. б) Вероятность поражения мишени стрелком при одном выстреле равна 0,95. Найти вероятность того, что при 50 выстрелах мишень будет поражена: 1) 45 раз; 2) более 45 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того. что Х примет значение x ₁ равно 0,7. Найти закон распределения Х, зная математическое ожидание М[ X ]=–0,5 и дисперсию D[ X ]=5,25.

7. Непрерывная случайная величина Х задана функцией распределения

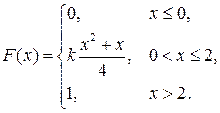
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =8 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 10); б) отклонения этой величины от математического ожидания не более, чем на d=1.

Вариант 2

1. Вычислить неопределенные интегралы:

а)	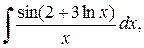б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)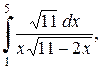

в) .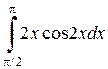

3. 10 вариантов контрольной работы распределены среди 8 студентов. Найти вероятность того, что варианты с номерами 1 и 2 не будут использованы?

4. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,8, 0,4 и 0,7. Определить вероятность того, что пройдут не менее двух посланных импульсов.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Монету бросают 6 раз. Найти вероятность того, что герб выпадет не более двух раз.

б) Вероятность появления события в серии испытаний постоянна и равна 0,2. Найти вероятность того, что при 400 испытаниях событие появится: 1) ровно 104 раза; 2) больше 70, но меньше 90 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,4. Найти закон распределения Х, зная математическое ожидание М[ X ] = 2,2 и дисперсию D[ X ] = 0,96.

7. Непрерывная случайная величина Х задана функцией распределения

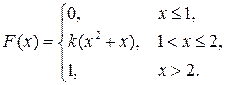
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =7 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 13); б) отклонения этой величины от математического ожидания не более, чем на d=2.

Вариант 3

1. Вычислить неопределенные интегралы:

а)	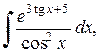б)
в)	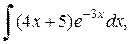г)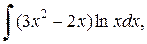
д)	е) .

2. Вычислить определенные интегралы:

а)

б)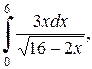

в) .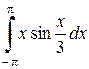

3. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее, чем на два из трех имеющихся в билете вопросов. Какова вероятность того, что студент сдаст зачет?

4. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,5, 0,4 и 0,3. Определить вероятность того, что пройдет хотя бы один из посланных импульсов.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Вероятность попадания в цель при одном выстреле из орудия р =0,85. Найти вероятность того, что в цель попадет не менее двух снарядов, если будет сделано 3 выстрела. б) В установленном технологическом процессе фабрика выпускает в среднем 75% продукции 1-го типа. Найти вероятность того, что в партии из 500 изделий окажется изделий 1-го типа: а) ровно 390, б) больше 370, но меньше 400.

6. Дан перечень возможных значений дискретной величины Х: x ₁=2, x ₂=4, x ₃=6, а также даны математическое ожидание этой величины M[ X ]=4,2 и ее квадрата M[ X ²]=19,6. Найти закон распределения случайной величины Х.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =6 и среднее квадратичное отклонение s=4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 8); б) отклонения этой величины от математического ожидания не более, чем на d=3.

Вариант 4

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. Зенитная батарея, состоящая из 5 орудий, производит залп по группе, состоящей из 3 самолетов. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному и тому же самолету.

4. Вероятность боя стеклянной тары при погрузке на автомашины равна 0,06, а при транспортировке – 0,05. Какова вероятность боя стеклянной тары?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Найти вероятность того, что при 4 испытаниях событие наступит ровно 2 раза, если вероятность его появления в каждом испытании равна 0,2. б) Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена: 1) ровно 85 раз; 2) не менее 70 и не более 80 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,4. Найти закон распределения Х, зная математическое ожидание М[ X ] = 0,4 и дисперсию D[ X ] = 3,84.

7. Непрерывная случайная величина Х задана функцией распределения

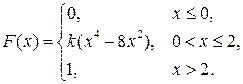
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =5 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 6); б) отклонения этой величины от математического ожидания не более, чем на d=4.

Вариант 5

1. Вычислить неопределенные интегралы:

а)	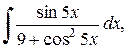б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. 10 вариантов контрольной работы распределяются случайным образом среди 10 студентов, сидящих в один ряд. Найти вероятность того, что варианты с номерами 1 и 2 достанутся рядом сидящим студентам.

4. В электроприборе вышел из строя некоторый элемент. Для его замены решили воспользоваться двумя списанными приборами. Вероятность того, что нужный элемент находится в рабочем состоянии равна 0,4 для каждого прибора. Найти вероятность того, что испорченный элемент будет заменен.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 10 выстрелах мишень будет поражена 5 раз. б) Монету бросают 300 раз. Найти вероятность того, что герб появится: 1) ровно 150 раз; 2) от 135 до 145 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того. что Х примет значение x ₁ равно 0,3. Найти закон распределения Х, зная математическое ожидание М[ X ] = 0,8 и дисперсию D[ X ] = 3,36.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =4 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 10); б) отклонения этой величины от математического ожидания не более, чем на d=4.

Вариант 6

1. Вычислить неопределенные интегралы:

а)	б)
в)	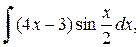г)
д)	е) .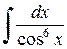

2. Вычислить определенные интегралы:

а)

б)

в) .

3. На полке в случайном порядке расставлено 10 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания (но не обязательно рядом).

4. На начальном участке для мотоциклиста-гонщика имеются 3 препятствия, вероятность остановки на каждом из которых равна 0,1. Вероятность остановки на заключительном участке равна 0,7. Какова вероятность того, что мотоциклист доедет до финиша без единой остановки?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Монету бросают 6 раз. Найти вероятность того, что герб выпадет не менее трех раз. б) Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 500 случайно отобранных деталей окажется непроверенных: 1) ровно110; 2) от 90 до 115.

6. Дан перечень возможных значений дискретной величины Х: x ₁=1, x ₂=3, x ₃=5, а также даны математическое ожидание этой величины M[ X ]=2,2 и ее квадрата M[ X ²]=6,6. Найти закон распределения случайной величины Х.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =3 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (4, 8); б) отклонения этой величины от математического ожидания не более, чем на d=3.

Вариант 7

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. На столе лежат 20 билетов. Какова вероятность того, что 3 наудачу взятых билета имеют номер не больше 5?

4. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производятся последовательно до наступления события. Определить вероятность того, что понадобится 4 опыта.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Стрелок производит три выстрела. Вероятность того, что он попадет в цель по крайней мере один раз, равна 0,992. Какова вероятность попадания в цель при одном выстреле?

б) Всхожесть семян определенного сорта растений равна 0,95. Найти вероятность того, что из 500 посаженых семян число проросших будет: 1) ровно 485; 2) не менее 470, но не более 480.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,3. Найти закон распределения Х, зная математическое ожидание М[ X ] = 0,1 и дисперсию D[ X ] = 1,89.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =2 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (6, 12); б) отклонения этой величины от математического ожидания не более, чем на d=3.

Вариант 8

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)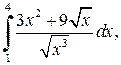

б)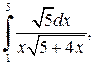

в) .

3. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных "в одну линию" кубиках можно будет прочесть слово " спорт ".

4. Вероятность сдать экзамен студентом равна 0,8. Какова вероятность того, что студент сдаст экзамен по крайней мере с третьей попытки?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Всхожесть семян составляет 70%. Определить вероятность того, что из 5 посеянных семян взойдет не менее 3.

б) Вероятность попадания стрелком в цель равно 0,85. Найти вероятность того, что при 150 выстрелах он попадет в цель: 1) ровно 120 раз; 2) не менее 125, но не более 135 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,9. Найти закон распределения Х, зная математическое ожидание М[ X ] = –0,7 и дисперсию D[ X ] = 0,81.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =2 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 6); б) отклонения этой величины от математического ожидания не более, чем на d=4.

Вариант 9

1. Вычислить неопределенные интегралы:

а)	б)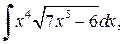
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .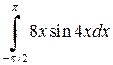

3. Брошены два игральных кубика. Какова вероятность, что сумма выпавших очков будет равна 7?

4. Предположим, что для одной торпеды вероятность попасть в цель равна 0,7. Какова вероятность того, что три торпеды потопят корабль, если для потопления достаточно одного попадания торпеды в цель?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) При передаче сообщения вероятность искажения одного знака равна 0,1. Какова вероятность того. что сообщение из 10 знаков содержит не более 3 искажений?

б) Было посажено 400 деревьев. Вероятность того, что отдельное дерево приживется равно 0,8. Найти вероятность того, что число прижившихся деревьев: 1) равно 300, 2) больше 310, но меньше 330.

6. Дан перечень возможных значений дискретной величины Х: x ₁=–2, x ₂=1, x ₃=4, а также даны математическое ожидание этой величины M[ X ]=2,5 и ее квадрата M[ X ²]=10,3. Найти закон распределения случайной величины Х.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =10 и среднее квадратичное отклонение s=4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (5, 9); б) отклонения этой величины от математического ожидания не более, чем на d=6.

Вариант 10

1. Вычислить неопределенные интегралы:

а)	б)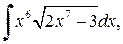
в)	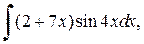г)
д)	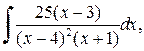е) .

2. Вычислить определенные интегралы:

а)

б)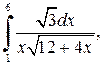

в) .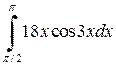

3. Пяти полевым радиостанциям разрешено во время учений работать на 6 радиоволнах. Выбор волны на каждой станции производится наудачу. Найти вероятность того, что будут использованы различные радиоволны.

4. Девушка забыла последнюю цифру номера телефона своего жениха и набрала ее наугад. Определить вероятность того, что ей придется набирать номер не более трех раз.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Вероятность появления некоторого события в каждом из 5 независимых опытов равна 0,2. Определить вероятность появления этого события по крайней мере 3 раза.

б) Всхожесть семян данного сорта растений составляет 90%. Найти вероятность того, что из 900 посаженых семян число проросших будет: 1) равно 800, 2) заключено между 805 и 820.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,3. Найти закон распределения Х, зная математическое ожидание М[ X ] = 2,7 и дисперсию D[ X ] = 0,21.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =9 и среднее квадратичное отклонение s=4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 10); б) отклонения этой величины от математического ожидания не более, чем на d=5.

Вариант 11

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)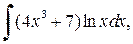
д)	е) .

2. Вычислить определенные интегралы:

а)

б)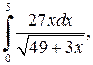

в) .

3. На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных "в одну линию" карточках, можно будет прочесть слово " трос ".

4. Вероятность брака из-за нарушения режима обработки деталей равна 0,02, а вследствие неисправности станка – 0,08. Какова вероятность выпуска бракованных деталей?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Вероятность хотя бы одного попадания стрелком в цель при 4 выстрелах равна 0,9919. Найти вероятность попадания в цель при одном выстреле, если вероятность попадания в цель при одном выстреле.

б) Посажено 600 семян кукурузы с вероятностью 0,9 прорастания для каждого семени. Найти вероятность того, что взойдет: 1) ровно 550 семян, 2) больше 535 и меньше 555.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,2. Найти закон распределения Х, зная математическое ожидание М[ X ] = 2 и дисперсию D[ X ] = 4.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =8 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 5); б) отклонения этой величины от математического ожидания не более, чем на d=5.

 

Вариант 12

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. Собрание, на котором присутствуют 25 человек, в том числе 15 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.

4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,26. Найти вероятность поражения цели первым из орудий, если известно, что вероятность попадания в цель вторым орудием при одном выстреле равна 0,9.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Каждое утро студент может опоздать на занятия с вероятностью 0,1. Сколько дней потребуется студенту, чтобы вероятность опоздания на занятия была равна 0,99.

б) Вероятность выхода из строя одного прибора равна 0,15. Найти вероятность того, что из 90 имеющихся приборов выйдет из строя: 1) ровно 10, 2) больше 15, но меньше 20.

6. Дан перечень возможных значений дискретной величины Х: x ₁=1, x ₂=2, x ₃=3, а также даны математическое ожидание этой величины M[ X ]=2,3 и ее квадрата M[ X ²]=5,9. Найти закон распределения случайной величины Х.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =3 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 5); б) отклонения этой величины от математического ожидания не более, чем на d=3.

Вариант 13

1. Вычислить неопределенные интегралы:

а)	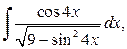б)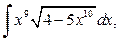
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. В замке на общей оси пять дисков, каждый из которых разделен на шесть секторов с различными написанными на них буквами. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.

4. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочнике соответственно равны 0,6, 0,8 и 0,9. Найти вероятность того, что формула содержится только в двух справочниках.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Известно, что при взвешивании равновозможно как положительная, так и отрицательная ошибка. Какова вероятность того, что при 5 взвешиваниях получатся 3 положительные ошибки.

б) Посажено 1200 семян фасоли с вероятностью прорастания 0,95. Найти вероятность того, что прорастет: 1) ровно 1150 семян, 2) не менее 1130, но не более 1160.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,3. Найти закон распределения Х, зная математическое ожидание М[ X ] = 1,5 и дисперсию D[ X ] = 5,25.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =4 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 8); б) отклонения этой величины от математического ожидания не более, чем на d=2.

Вариант 14

1. Вычислить неопределенные интегралы:

а)	б)
в)	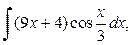г)
д)	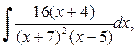е) .

2. Вычислить определенные интегралы:

а)

б)

в) .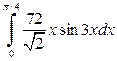

3. Случайным образом выписаны 3 цифры. Найти вероятность того, что: а) все выписанные цифры одинаковые; б) все цифры различные; в) среди выписанных цифр ровно две совпадают.

4. Разрыв электрической цепи может произойти вследствие выхода из строя элемента А или двух элементов В и С, которые выходят из строя независимо друг от друга соответственно с вероятностями 0,3, 0,2 и 0,1. Определить вероятность разрыва цепи.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Студентам на контрольной работе предложено 10 вопросов, но каждый из которых дается правильный и неправильный ответ. Для получения хорошей оценки нужно указать не менее 80% правильных ответов. Какова вероятность получения хорошей оценки при простом отгадывании?

б) Посажено 500 семян гороха с вероятность прорастания 0,9. Найти вероятность того, что прорастет: 1) ровно 450 семян, 2) не менее 440, но не более 460 семян.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,1. Найти закон распределения Х, зная математическое ожидание М[ X ] = 3 и дисперсию D[ X ] = 9.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =1 и среднее квадратичное отклонение s=6 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 9); б) отклонения этой величины от математического ожидания не более, чем на d=4.

Вариант 15

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .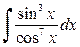

2. Вычислить определенные интегралы:

а)

б)

в) .

3. На полке в случайном порядке расставлено 10 книг, среди которых находится двухтомник Дж. Лондона. Найти вероятность того, что оба тома двухтомника расположены рядом.

4. Вероятность того, что данный спортсмен улучшит свой предыдущий результат с одной попытки, равна 0,6. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Общее число опытов равно 5. Найти вероятность того, что не менее чем в 3-х опытах получится удачный результат.

б) Вероятность поражения мишени стрелком при одном выстреле равна 0,85. Найти вероятность того, что при 90 выстрелах мишень будет поражена: 1) 75 раз; 2) не менее 73, но не более 83 раз.

6. Дан перечень возможных значений дискретной величины Х: x ₁=–3, x ₂=2, x ₃=3, а также даны математическое ожидание этой величины M[ X ]=1,8 и ее квадрата M[ X ²]=6. Найти закон распределения случайной величины Х.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =2 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (6, 11); б) отклонения этой величины от математического ожидания не более, чем на d=4.

Вариант 16

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	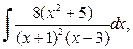е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. В одной урне 3 белых и 5 черных шаров, в другой – 5 белых и 2 черных. Из каждой урны взяли по шару. Какова вероятность того, что шары будут одного цвета?

4. Вероятность поражения мишени, если по ней делают по одному выстрелу два стрелка, равна 0,82. Определить вероятность попадания в цель при одном выстреле для первого стрелка, если вероятность попадания для второго стрелка равна 0,7.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) В магазин вошли 8 покупателей. Найти вероятность того, что трое из них совершат покупки, если вероятность совершить покупку для каждого покупателя одна и та же и равна 0,3.

б) Вероятность появления события в серии испытаний постоянна и равна 0,3. Найти вероятность того, что при 250 испытаниях событие появится: 1) ровно 80 раза; 2) больше 65, но меньше 85 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,4. Найти закон распределения Х, зная математическое ожидание М[ X ] = 3,4 и дисперсию D[ X ] = 3,84.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =8 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 10); б) отклонения этой величины от математического ожидания не более, чем на d=9.

Вариант 17

1. Вычислить неопределенные интегралы:

а)	б)
в)	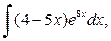г)
д)	е) .

2. Вычислить определенные интегралы:

а)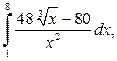

б)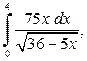

в) .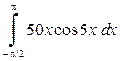

3. Зенитная батарея, состоящая из 3 орудий, производит залп по группе, состоящей из 5 самолетов. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по различным самолетам.

4. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,7, 0,5 и 0,6. Определить вероятность того, что пройдут только два посланных импульса.

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Монету бросают 8 раз. Найти вероятность того, что герб выпадет не более трех раз.

б) В установленном технологическом процессе фабрика выпускает в среднем 80% продукции марки А. Найти вероятность того, что в партии из 900 изделий окажется изделий марки А: а) ровно 700, б) больше 710, но меньше 740.

6. Дискретная случайная величина Х имеет только два возможных значения: x ₁ и x ₂, причем x ₁ < x ₂. Вероятность того, что Х примет значение x ₁ равно 0,2. Найти закон распределения Х, зная математическое ожидание М[ X ] = 0,2 и дисперсию D[ X ] = 2,56.

7. Непрерывная случайная величина Х задана функцией распределения

Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а =7 и среднее квадратичное отклонение s=4 нормально распределенной с

Поделиться:

Воспользуйтесь поиском по сайту: