 |
Эффект Доплера для звуковых волн
|
|
|
|
Интерференция в тонких пленках. Полосы равной толщины и равного наклона.
8. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля на круглом отверстии.
9. Дифракция Фраунгофера. Дифракционная решетка. Условие минимума и максимума дифракции. Дифракция на кристаллических решетках.
10. Применение дифракции и интерференции. Просветление оптики. Спектральный анализ. Голография.
11. Поляризация света. Естественный и поляризованный свет. Степень поляризации. Закон Малюса. Вращение пл-сти поляризации.
12. Способы получения поляризованного света. Двойное лучепреломление. Дихроизм. Яв-ие и закон Брюстера. Искусственная анизотропия.
Поляризация света при отражении и преломлении на поверхности диэлектриков. Формулы Френеля.
14. Тепловое излучение. Основные характеристики теплового излучения. Законы теплового излучения. Пр-да теплового излучения. Характеристики теплового излучения: поток, энергетическая светимость, спектральная плотность энергетической светимости, поглощательная способность. Абсолютно черное тело. Экспериментальные законы Кирхгофа и Стефана-Больцмана. Закон смещения Вина.
Формула Планка для спектральной плотности энергетической светимости абсолютного черного тела.
16. Фотоэффект и его законы. Пр-да внешнего фотоэффекта. Ур-ние Эйнштейна для внешнего фотоэффекта. Красная граница фотоэффекта. Работа выхода электрона из металла. Применение фотоэффекта.
17.Масса и импульс фотона. Давление света. Корпускулярные св-ва света. Возможность определения массы и импульса фотона. Давление света – как проявление корпускулярных св-в. Взаимосвязь с энергией фотонов и св-вом пов-сти. Квантовое и волновое объяснение давления света.
|
|
|
1. Волны в упругой среде. Механизм распределения в упругой среде. Продольные и поперечные волны. Фронт волны и волновая пов-сть. Плоские, сферические и цилиндрические волны. Скорость распространения волн. Ур-ние плоской и сферической волн.
Волной наз-ют процессы распределения колеб-ий в сплошной среде.
Распространение колебаний в упругих средах происходит за счет упругих (мех-ских) волн, переносят энергию и импульс без переноса в-ва. Упругими наз-ся мех-ие волны, при котором распространяется деформация в упругой среде.
В продольной волне точка среды смещ-ся вдоль направления распр. волны. Волны такого типа возникают в средах при деформации растяж/сжат
Поперечные волны распр-ся в средах, вк-ых возможны деформации сдвига.
Частицы среды колеблются в направлении, перпендикулярном направлению распространения волн.
Геометрическое место точек в пространстве, до которых распространяется возмущение среды к моменту времени t наз-тся фронтом волны.
Геометрическое место точек, колеблющихся в одинаковой фазе, наз-тся
волновой поверхностью. Волновой фронт является частным случаем
волновой поверхности. Если волновые поверхности имеют вид плоскостей параллельных друг другу – волна наз-тся плоской. Если волновая поверхность –имеет вид концентрических сфер, то волна наз-тся сферической. Если цилиндра – волна цилиндрическая.
Скорость распространения волн тем меньше, чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле:
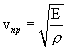, а поперечной: 
где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Для большинства твердых тел E>G поэтому скорость продольных волн больше скорости поперечных.
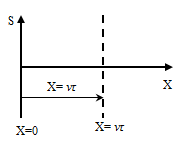Уравнение плоской волны:
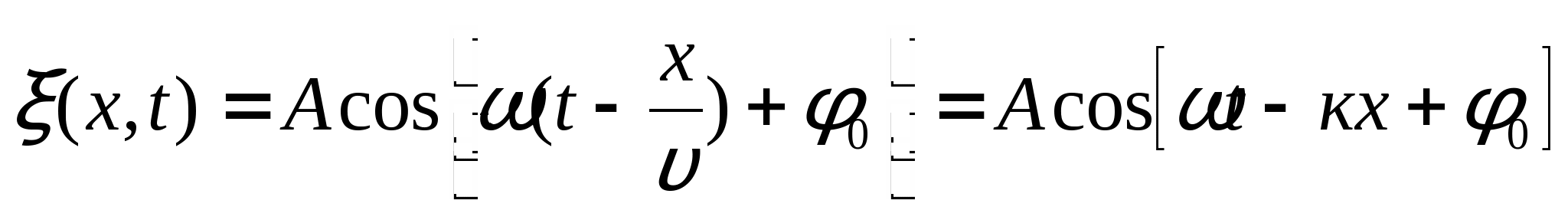
Уравнение сферической волны:
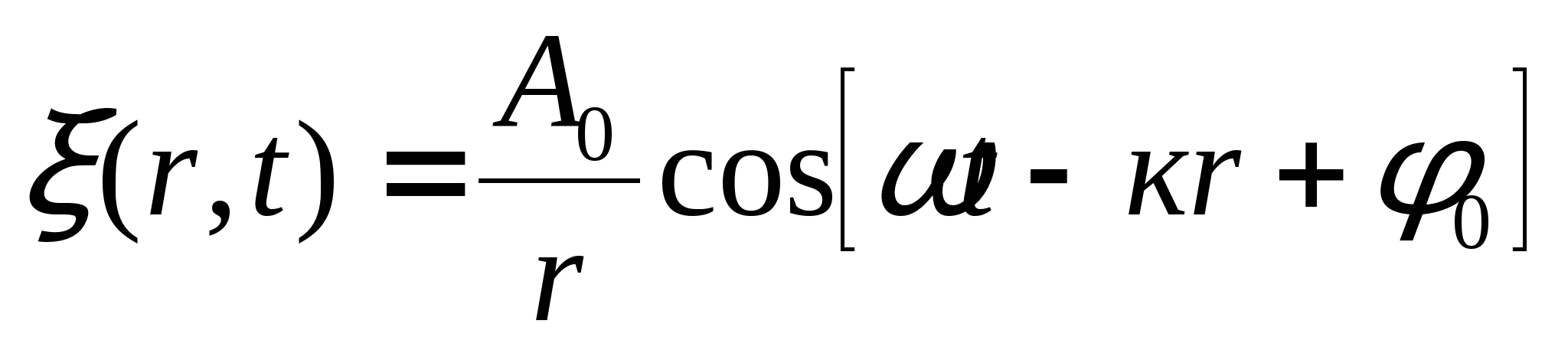
ξ - смещение точки от положения равновесия в плоскости, находящейся на расстоянии х от источника колебаний;
|
|
|
А - амплитуда волны;
φ0 - начальная фаза.
2. Энергия упругой волны. Энергия упругой волны. Поток и плотность потока энергии. Вектор Умова. Звуковые волны. Эффект Доплера для звуковых волн.
Энергия волны в упругой среде состоит из кинетической энергии частиц в-ва, совершающих небольшие колебания, и из потенциальной энергии упругой деформации среды.
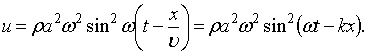
Плотность кинетической энергии:
|
|
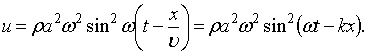
Средняя плотность энергии
|
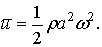
Плотность энергии и ее среднее значение пропорциональны плотности среды ρ, квадрату частоты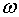 
и квадрату амплитуды волны а.
Кол-во энергии, переносимое волной через некоторую поверхность в единицу времени, наз-тся потоком энергии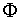 
через поверхность. Поток энергии — скалярная величина, размерность [Вт].
Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики течения энергии в разных точках пространства используют векторную величину, наз-мую плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку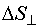 
, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия ΔE за единицу времени Δt. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Плотность потока энергии j равна
 =˃ 
|
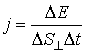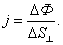
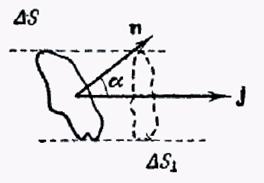Вектор плотности потока энергии наз-тся вектором Умова.
Вектор различен в разных точках пространства, а в данной точке пространства изменяется со временем по закону квадрата синуса. Среднее значение его с учетом 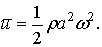равно 
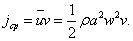
Звуковая волна (звуковые колебания) – это передающиеся в пространстве механические колебания молекул в-ва. В результате возмущений, вызывающих движение и колебания воздуха в определенной точке пространства, возникает перепад давления в этом месте, так как воздух в процессе движения сжимается, в результате чего возникает избыточное давление, толкающее окружающие слои воздуха. Эти слои сжимаются, что в свою очередь снова создает избыточное давление, влияющее на соседние слои воздуха. Так по цепочке, происходит передача первоначального возмущения в пространстве из одной точки в другую. Тело, создающее колебания воздуха, наз-ют источником звука.
|
|
|
Эффект Доплера наз-тся изменение v колебаний, воспринимаемой приемником при движении источника этих колебаний и приемника друг относительно друга.
Эффект Доплера для звуковых волн
Скорость источника Vист будем считать с (+), если источник движется к приемнику, и с (-) если источник движется от приемника. Также скорость приемника Vпр будем считать с (+), если приемник движется к источнику, и с (-) если приемник движется от источника.
3. Отражение и преломление упругих волн. Принцип Гюйгенса. Стоячие волны. Интерференция волн и дифракция упругих волн.
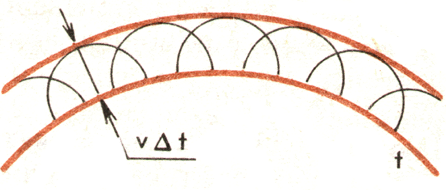Принцип Гюйгенса: каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени см. рис.
Для механических волн принцип Гюйгенса имеет определенное значение: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.
Уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:
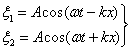
Сложив вместе эти ур-ния и преоб-вав результат по ф-ле для суммы косинусов:
Преобразовав это уравнение, получим уравнение стоячей волны:
Законы отражения и преломления справедливы только при условии, что протяженность границы раздела значительно превышает длину волны λ. Если это условие не выполняется, то существенное значение играет дифракция волн, которая проявляется в огибании волнами препятствия. Представим, что плоская волна приближается к преграде, имеющей точечное отверстие (рис.1.8). Максимумы приходящей волны производят периодическое возмущение в отверстии преграды. Это возмущение порождает сферическую волну согласно принципу Гюйгенса. Волновая картина, возникающая за преградой, состоит из набора сферических волн, расходящихся от отверстия.
|
|
|
При сложении волн с одинаковой частотой, т.е. с постоянной разностью фаз возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливаются, а в других точках ослабляются. Таким образом, результатом интерференции является перераспределение границы раздела
энергии упругих волн в пространстве. Волны, для которых возможно
наблюдать интерференцию, носят название когерентные волны - это волны,
которые имеют одинаковую частоту и постоянную во времени разность фаз. Пусть в искомой точке пространства складываемые колебания имеют вид
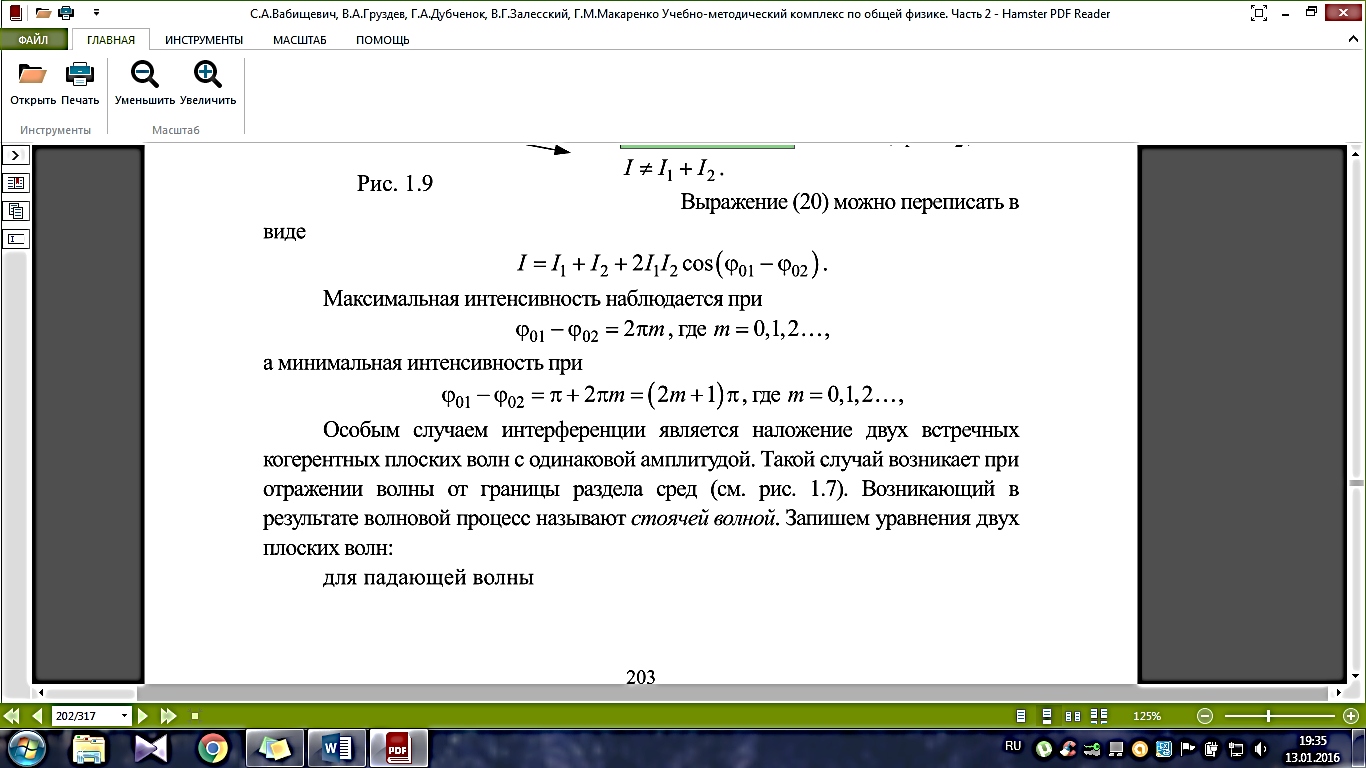
4. Геометрическая оптика. Принцип Ферма. Законы геометрической оптики. Абсолютный и относительный показатели преломления. Линзы.
При́нцип Ферма́ — луч, распространяющийся между двумя точками, выбирает путь, требующий минимального времени.
Время прохождения лучом пути ADB:
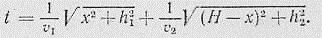
Условие экстремума времени запишется так:
Отсюда сразу же получается правильный закон преломления.
|
|
|
