 |
Прямой, обратный и дополнительный коды.
|
|
|
|
Формы представления чисел в ЭВМ.
Для представления чисел в ЭВМ применяются две различные формы: с фиксированной точкой (запятой) - для целых чисел и с плавающей точкой (запятой) для действительных чисел.
Целые числа могут быть представлены со знаком и без знака.
Возьмем разрядную сетку из 8 бит (т.е. байт) и попробуем разобраться, как представляются целые числа без знака. Самое маленькое число, которое можно поместить в один байт без знака — это ноль.
Число 0 без знака.
Самое большое число, которое можно представить в одном байте без знака — это (в двоичном виде) 111111112
Переведем это число в десятичную систему счисления (для простоты счета переведем сначала в 8-ную).
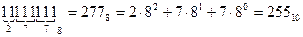
Итак, в один байт без знака можно поместить максимальное десятичное число 255.
Аналогично можно вычислить максимальное число, которое можно поместить в два байта (т.е. 16 бит).
11111111111111112=6553510.
Для чисел со знаком самый левый разряд отводится под знак. Для положительного числа этот разряд равен 0, для отрицательного — 1.
Число +12 в 8-битной разрядной сетке будет записано следующим образом: 1210=11002.

Знак ‘+’
Обратите внимание на расположение чисел в разрядной сетке: между знаковым разрядом и первым значащим разрядом числа располагаются нули.
Вычислим максимальное положительное число, которое помещается в 8 бит со знаком, т.е. под число отводится 7 бит.
знак
|
|
|
11111112=1778=1.82+7.81+1.80=64+56=127.
Теперь вычислим максимальное положительное число, которое помещается в 16-ти разрядную сетку со знаком.
знак
1111111111111112=7FFF16=716.163+F16.161+F16.161+F16.160=7.163+15.162+15.161+15.1=32767.
Представление отрицательных чисел существенно отличается от представления положительных чисел. Предварительно рассмотрим некоторые понятия, а именно введем определение прямого, обратного и дополнительного кодов.
Прямой, обратный и дополнительный коды.
1) Положительные числа.
Для положительных чисел прямой код равен обратному коду и равен дополнительному коду.
Прямой код Xпр двоичного числа X содержит двоичные цифровые разряды, слева записывается знак числа.
Пример.
Разместить в разрядной сетке из восьми разрядов положительное число 97.
9710=11000012.
Это же число разместим в разрядной сетке из 16 разрядов.
2) Отрицательные числа.
Отрицательные числа хранятся в памяти ЭВМ либо в обратном, либо в дополнительном кодах.
Обратный код Xобр двоичного отрицательного числа X получается следующим образом: в знаковый разряд числа записывается единица, в цифровых разрядах нули заменяются единицами, а единицы — нулями.
Запишем число -4 в обратном коде в 8-ми разрядной сетке. Двоичный код модуля исходного числа равен 1002. Обратный код получается инверсией каждого разряда двоичного кода модуля исходного числа, записанного в 8-ми разрядную сетку.
Двоичный код модуля исходного числа равен 00000100. Выполним инверсию каждого разряда.
Обратный код числа -4 записывается следующим образом:

Знаковый разряд
Дополнительный код Xдоп отрицательного числа X получается из обратного кода Xобр путем прибавления единицы к самому правому разряду (он называется младшим).
|
|
|
Итак, Xдоп=Xобр + 00000001, т.е.
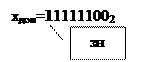 1 1
| |||||||
| (знак.разряд) | |||||||
(сложение производим в двоичной системе счисления 12+12=102)
1 1 1 1 1 1 0 0
2726252423222120
Теперь приведем полученное число в десятичную систему счисления
128+64+32+16+8+4=252
Мы получили, что дополнительный код числа –4 в десятичной системе счисления равен 252. Сложим ê-4ê+252=256. 256=28. Количество разрядов сетки было равно 8. Число 252 «дополнило» число ç–4ç до 28 = 1000000010.
Теперь сложим два двоичных числа – двоичный код числа ç-4ç в 8-разрядной сетке и дополнительный код числа –4:
 11111100
11111100
 1 000000002 мы получили 28
1 000000002 мы получили 28
Запишем общее правило получения дополнительного кода некоторого целого числа х.
 x, x>=0
x, x>=0
Xдоп =
2k - |x|, x<0, где k – количество разрядов сетки.
Есть еще одно очень простое правило получения дополнительного кода некоторого отрицательного числа.
Для получения дополнительного кода, необходимо инвертировать все разряды прямого кода модуля исходного числа начиная с самого левого разряда исключая последнюю единицу и стоящие за ней нули.
00000 100 прямой код ç-4ç
11111 100
инверсия разрядов
Исходя из вышеизложенного, можно определить, что самое маленькое отрицательное число, которое можно записать в 8-ми разрядной сетке — -128, а в 16-ти разрядной сетке — -32768.
|
|
|


