Вопрос 26 Интервалы прогноза по линейному уравнению регрессии

Вопрос 23 Доверительные интервалы

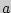Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.Для оценки математического ожидания случайной величины 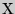, распределенной по нормальному закону, при известном среднем квадратическом отклонении 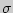служит доверительный интервал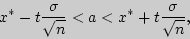
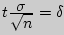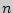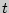где - точность оценки, - объем выборки, - выборочное среднее, - аргумент функции Лапласа, при котором

Вопрос 24 F критерий

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: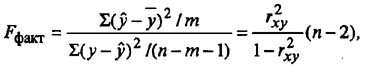 где n - число наблюдений;
m - число параметров при факторе х.F табличный - это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.Уровень значимости а - вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Вопрос 25 Таблица дисперсионного анализа для линейной регрессии

Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера. Перед расчетом критерия проводится дисперсионный анализ.Общая сумма квадратов отклонений у от его среднего значения раскладывается на объясненную и остаточную регрессии: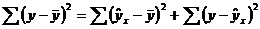 общая объяснен остаточнаяЕсли фактор не оказывает влияние на результат, то теоретические значения будут равны среднему. 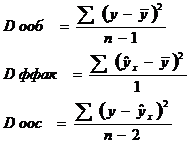Разделив суммы квадратов на соответствующее число степеней свободы, получили дисперсии:
Расчетное значение критерия Фишера находится по формуле: 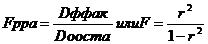Fтабл. определяется по таблицам распределения Фишера с учетом уровня значимости ά=0,05/0,01/0,1 и числом степеней свободы ν1 = 1, ν2=n-2. Если Фрасч>Фтабл, уравнение регрессии признается значимым.Значимость уравнения множественной регрессии оценивается с помощью Ф-критерия Фишера: M – число параметров при хФтабл при α=0,05 V1=m V2=n-m-1Факт>Фтабл уравнение значимо.Можно оценить значимость не только уравнения в целом, но и фактора дополнительно включенного в модель. Для этого определяется частный Ф критерий. Оценим значимость влияния х1 как дополнительно включенного фактора: 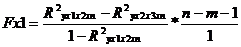R2yx1x2xn – коэффициент множественной детерминации для модели с полным набором факторовR2yx2x3xn - коэффициент множественной детерминации для модели без учета Х1Фх1 сравнивается с Фтабл при α=0,05 V1=1 V2=n-m-1Фх1>Фтабл – дополнительное включение фактора Х1 в модель статистики оправдано и коэффициент чистой регрессии b1 статистики значим.Фх1<Фтабл – фактор Х1 нецелесообразно включать в модель и коэффициент чистой регрессии статистики незначим

Вопрос 26 Интервалы прогноза по линейному уравнению регрессии

Для каждой точки на линии регрессии можно построить доверит интервалы свероятностью р=1-a=0,95, так, что они будут лежать в этих интервалах. yтеор (хср)=a*+(b*)*хср (2)Линия регрессии проходит точно через т. (хср;yср). a*= yср - (b*)*xср (3)Подставляем в (1): yтеор (хр)= yср + (b*)* (хр- xср).Цель: выяснить дисперсию этого значения m2 yтеор (хр)=D yтеор (хр)= D yср + D((b*)*(хр- xср)) - cov(yср +(b*)* (хр- xср)), где m – среднеквадратич отклонение. Если переменныенеизменны, cov=0. cov (x;y)=(åi от 1 до n (xi-xср)*(yi-yср))/n. m2 yтеор (хр)= D yср+(xр-xср)2*Db*= m2 ycр+ (m2 b*)*((xр-xср)2 m2 ycр @ d2yср/n @ S2ост/((n-2)*n) ------- оценка m2 b*@d2yср*1/(åi от 1 до n (xi-xср)2)@ S2ост/((n-2)*(åi от 1 до n (xi-xср)2) myтеор (хср)=Корень квадр из (S2ост/(n-2))*корень квадр из(1/n+(xр-xср)2/(åi от 1 до n (xi-xср)2)).Для среднеквадратич отклонения точки, лежащей на линии регрессии на осиабсцисс т.х прогнозное. txp = (yтеор (хр)-a-b*xp)/ myтеор (хр) – распределена по закону Стьюдентаg(число степеней свободы для парной линейной регрессии)=n-2.a=0,05, 1-a=0,95

Поделиться:

Воспользуйтесь поиском по сайту: