 |
Древовидные и решетчатые диаграммы.
|
|
|
|
Для большей наглядности таблицу 2 можно отобразить диаграммой рис. 7. Построение диаграммы начинаем с точки  и будем применять следующее правило:
и будем применять следующее правило:
если на вход кодера первым информационным символом будет подана единица (1), то через точку  проводим небольшой отрезок, направленный вниз.
проводим небольшой отрезок, направленный вниз.
если бы первым информационным символом был 0, то этот вертикальный отрезок направили бы вверх от точки  .
.
Так как первый информационный символ, подаваемый на вход, есть 1, то вертикальный отрезок, проходящий через точку  , согласно правилу, направляем вниз. Этот единичный символ, подаваемый на вход кодера, согласно таблице 2 является причиной появления на выходе кодовой последовательности из двух символов 11; поэтому из конца вертикального отрезка проводим горизонтальный отрезок, который обозначаем, как 11.
, согласно правилу, направляем вниз. Этот единичный символ, подаваемый на вход кодера, согласно таблице 2 является причиной появления на выходе кодовой последовательности из двух символов 11; поэтому из конца вертикального отрезка проводим горизонтальный отрезок, который обозначаем, как 11.

Рис. 7 Диаграмма выходных символов (ими обозначены горизонтальные отрезки),
как реакция кодера на входные символы (ими обозначены вертикальные отрезки).
Так как второй информационный символ, поступающий на вход снова - есть 1, то, согласно правилу, из конца первого горизонтального отрезка проводим вертикальный отрезок, направленный снова вниз. Поступивший на вход кодера второй информационный символ согласно таблице 2 является причиной появления на выходе кодера последовательности 01 и поэтому горизонтальный отрезок, проведенный из конца второго вертикального отрезка, обозначаем как 01 и т.д. Начиная с 4-го символа, на вход подаются нулевые символы, и поэтому вертикальные отрезки, соответствующие этим символам, направляем вверх. В результате получаем всю диаграмму, изображенную на рис. 7.
Если, вместо взятой в данном примере входной последовательности информационных символов, на вход кодера подадим другую последовательность, то таблица заполнится другими символами, и им будет соответствовать другая диаграмма. Всевозможные диаграммы можно объединить в одну общую диаграмму (рис. 8), которую назовем древовидной диаграммой для сверточного кода, а исходные диаграммы будут являться ветвями этого дерева. Так диаграмме, изображенной на рис. 7, на общей древовидной диаграмме рис. 8 соответствует ветвь, обозначенная пунктиром. Т.е., если на вход кодера поступают информационные символы 111000, то на выходе кодера получаем: 11 01 10 01 11 00.
|
|
|
Еще раз напомним, что при построении диаграммы рис. 8 и таблицы 2 предполагается, что первоначально ячейки регистра сдвига содержали одни нули.
На рис. 8 видно, что древовидная диаграмма состоит из узлов и ребер. Узлы – это точки, которые обозначены буквами:  и
и  . Узлы также называют состояниями кодера. Ребра - это горизонтальные отрезки, над которыми стоят обозначения 00,01,10 или 11.
. Узлы также называют состояниями кодера. Ребра - это горизонтальные отрезки, над которыми стоят обозначения 00,01,10 или 11.
Появление любой из этих комбинаций на выходе кодера зависит от состояния кодера, т.е. от того, из какого узла  или
или  выходят ребра, и от того, какой информационный символ 0 или 1 поступает на вход кодера. Под состоянием кодера (рис. 1) можно понимать состояние первой и второй ячейки регистра сдвига перед подачей информационного символа на вход кодера или также можно понимать состояние второй и третьей ячейки после подачи информационного символа. Имеет место, что при подаче на вход информационного символа, символ, который был до этого в первой ячейке, смещается во вторую, а тот, который был во второй, смещается в третью ячейку регистра.
выходят ребра, и от того, какой информационный символ 0 или 1 поступает на вход кодера. Под состоянием кодера (рис. 1) можно понимать состояние первой и второй ячейки регистра сдвига перед подачей информационного символа на вход кодера или также можно понимать состояние второй и третьей ячейки после подачи информационного символа. Имеет место, что при подаче на вход информационного символа, символ, который был до этого в первой ячейке, смещается во вторую, а тот, который был во второй, смещается в третью ячейку регистра.
В дальнейшем, чтобы исключить возможную путаницу будем всегда понимать под состоянием кодера содержание второй и третьей ячеек после подачи информационного символа. В общем случае, когда кодовое ограничение  под состоянием кодера будем понимать содержание последних
под состоянием кодера будем понимать содержание последних 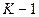 ячеек регистра сдвига после подачи информационного символа.
ячеек регистра сдвига после подачи информационного символа.
|
|
|
Итак, состояния кодера (рис. 1) могут принимать следующие значения: 00,10,01 или 11 и эти состояния соответствуют узлам  и
и  , т.е.
, т.е. 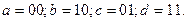

Из древовидной диаграммы видно, что при росте длины входной информационной последовательности число узлов на дереве растет как 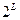 , а число ребер как
, а число ребер как 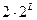 ,где
,где  - номер уровня на диаграмме (рис. 8), т.е. чрезвычайно быстро, что является существенным недостатком древовидных диаграмм. Заметим, что величина
- номер уровня на диаграмме (рис. 8), т.е. чрезвычайно быстро, что является существенным недостатком древовидных диаграмм. Заметим, что величина 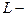 связана с номе-
связана с номе-

Рис. 8 Древовидное представление кодера рис. 1.
ром  информационного символа, подаваемого на вход кодера, простым соотношением
информационного символа, подаваемого на вход кодера, простым соотношением 
В 1967 году Д.Форни удалось преодолеть этот недостаток. Он обратил внимание на то, что ребра, выходящие из любых двух вершин древовидной диаграммы, которым соответствуют одинаковые состояния (например, состояние  ), полностью тождественны. Это является причиной того, что, начиная с уровня 3, верхнее и нижнее поддеревья также одинаковы, поэтому их можно отождествить. В результате вместо древовидной диаграммы Д.Форни получил решетчатую диаграмму, изображенную на рис. 9, в которой отмеченный выше недостаток древовидной диаграммы отсутствует. Решетчатая диаграмма также состоит из ребер и узлов.
), полностью тождественны. Это является причиной того, что, начиная с уровня 3, верхнее и нижнее поддеревья также одинаковы, поэтому их можно отождествить. В результате вместо древовидной диаграммы Д.Форни получил решетчатую диаграмму, изображенную на рис. 9, в которой отмеченный выше недостаток древовидной диаграммы отсутствует. Решетчатая диаграмма также состоит из ребер и узлов.

Рис. 9 Решетчатая диаграмма кодера.
Все узлы решетки, расположенные вдоль верхней горизонтали имеют одно и тоже состояние  Узлы, расположенные вдоль второй горизонтали, также имеют одно состояние
Узлы, расположенные вдоль второй горизонтали, также имеют одно состояние  Вдоль третьей горизонтали узлы имеют состояние
Вдоль третьей горизонтали узлы имеют состояние  и вдоль четвертой горизонтали состояние
и вдоль четвертой горизонтали состояние 
При построении решетки, как и при построении древовидной диаграммы (рис. 8) предполагается, что первоначально ячейки регистра сдвига кодера содержали одни нули,
т.е. вначале кодер находится в состоянии  Поэтому построение решетки начинается с левого узла
Поэтому построение решетки начинается с левого узла  (в верхней горизонтали решетки).
(в верхней горизонтали решетки).
Если на вход кодера, находящегося в состоянии  , поступает информационный символ 0 или 1. то на выходе появляются соответственно кодовые символы 00 или 11. Поэтому из узла
, поступает информационный символ 0 или 1. то на выходе появляются соответственно кодовые символы 00 или 11. Поэтому из узла  проводим два ребра, обозначенных соответственно 00 и 11. При этом ребро 00, соответствующее отклику кодера на символ 0 идет выше ребра 11, соответствующего отклику кодера на символ 1. Это соответствует расположению аналогичных ребер на древовидной диаграмме, где ребро 00 расположено выше ребра 11.
проводим два ребра, обозначенных соответственно 00 и 11. При этом ребро 00, соответствующее отклику кодера на символ 0 идет выше ребра 11, соответствующего отклику кодера на символ 1. Это соответствует расположению аналогичных ребер на древовидной диаграмме, где ребро 00 расположено выше ребра 11.
|
|
|
На решетчатой диаграмме для усиления различия откликов на 0 и 1, ребра, обозначающие эти отклики, будем изображать сплошной линией и пунктирной линией соответственно.
Таким образом, на уровне 0 обе диаграммы (древовидная и решетчатая) в качественном отношении полностью соответствуют друг другу.
Это соответствие также проявляется и для 1-го и 2-го уровней. На обеих диаграммах на 1-ом уровне имеется два узла  и
и 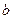 , из которых выходят 4-е ребра. Из узла
, из которых выходят 4-е ребра. Из узла  выходят ребра 00 и 11, причем ребро 00 (это отклик кодера на нулевой информационный символ) идет выше ребра 11 (поскольку это отклик на единичный символ). Из узла
выходят ребра 00 и 11, причем ребро 00 (это отклик кодера на нулевой информационный символ) идет выше ребра 11 (поскольку это отклик на единичный символ). Из узла 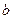 выходят ребра 10 и 01. Ребро 10 – это отклик кодера на нулевой символ и это ребро идет выше ребра 01, которое является откликом кодера на единичный символ. Тоже соответствие для обеих диаграмм проявляется и для 2-го уровня, на котором уже задействовано 4-е узла с состояниями
выходят ребра 10 и 01. Ребро 10 – это отклик кодера на нулевой символ и это ребро идет выше ребра 01, которое является откликом кодера на единичный символ. Тоже соответствие для обеих диаграмм проявляется и для 2-го уровня, на котором уже задействовано 4-е узла с состояниями  и
и  .
.
Различие между диаграммами, начиная с 3-го уровня, носит принципиальный характер. На древовидной диаграмме на 3-ем уровне расположено 8-м узлов: два узла « », два узла «
», два узла «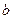 », два узла «
», два узла « » и два узла «
» и два узла « », а на решетчатой диаграмме на 3-ем уровне количество узлов не изменилось по сравнению со 2-м уровнем, т.е. осталось равным 4-м.
», а на решетчатой диаграмме на 3-ем уровне количество узлов не изменилось по сравнению со 2-м уровнем, т.е. осталось равным 4-м.
Два узла « » на древовидной диаграмме отождествляются и превращаются в один узел «
» на древовидной диаграмме отождествляются и превращаются в один узел « » на решетчатой диаграмме. Аналогично происходит и с другими узлами «
» на решетчатой диаграмме. Аналогично происходит и с другими узлами «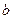 », «
», « » и «
» и « ».
».
На 4-м уровне на древовидной диаграмме отождествляются четыре узла « », четыре узла «
», четыре узла «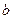 », четыре узла «
», четыре узла « » и четыре узла «
» и четыре узла « » и превращаются соответственно в один узел «
» и превращаются соответственно в один узел « », один узел «
», один узел «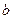 », один узел «
», один узел « » и один узел «
» и один узел « » на решетчатой диаграмме.
» на решетчатой диаграмме.
В отличие от древовидной диаграммы в результате описанных отождествлений получается решетчатая диаграмма, на которой на любом уровне после 3-го имеется всего 4-е узла.
В общем случае (при любом  ) число вершин в решетчатой диаграмме не растет, а остается равным
) число вершин в решетчатой диаграмме не растет, а остается равным  (где
(где  длина кодового ограничения). В рассматриваемом примере кодера
длина кодового ограничения). В рассматриваемом примере кодера 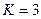 , поэтому получаем
, поэтому получаем  На древовидной диаграмме, как уже отмечалось, при увеличении номеров уровней происходит катастрофический рост числа узлов и соответственно ребер, что делает древовидные диаграммы менее привлекательными для практического использования, особенно при декодировании.
На древовидной диаграмме, как уже отмечалось, при увеличении номеров уровней происходит катастрофический рост числа узлов и соответственно ребер, что делает древовидные диаграммы менее привлекательными для практического использования, особенно при декодировании.
|
|
|
По заданной последовательности входных информационных символов (ИС) с помощью решетчатой диаграммы и по древовидной диаграмме легко определить последовательность кодовых символов (ПКС) на выходе кодера. Так, например, для последовательности 111000 входных символов с помощью решетчатой диаграммы на основе использования изложенных выше правил движения по решетке, получаем кодовую последовательность 11 01 10 01 11 00, которая, естественно, совпадает с кодовой последовательностью, полученной по древовидной диаграмме. Данной кодовой последовательности на решетчатой диаграмме соответствует путь, обозначенный точками (рис 9).
Этот путь получается следующим образом. Движение по решетке начинаем с расположенного слева узла  . Так как на вход кодера поступает единичный ИС, то этому символу на диаграмме соответствует пунктирное ребро, выходящее из узла
. Так как на вход кодера поступает единичный ИС, то этому символу на диаграмме соответствует пунктирное ребро, выходящее из узла  и идущее в узел с состоянием
и идущее в узел с состоянием 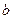 . Этому ребру на диаграмме соответствуют символы 11, которые и появляются на выходе кодера. Следующим ИС снова является 1, и ему на диаграмме также соответствует пунктирное ребро, выходящее из узла с состоянием
. Этому ребру на диаграмме соответствуют символы 11, которые и появляются на выходе кодера. Следующим ИС снова является 1, и ему на диаграмме также соответствует пунктирное ребро, выходящее из узла с состоянием 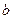 и идущее в узел с состоянием
и идущее в узел с состоянием  . Этому ребру на диаграмме соответствуют символы 01, появляющиеся на выходе кодера. Третий ИС также является 1, поэтому ему снова соответствует пунктирное ребро из узла с состоянием
. Этому ребру на диаграмме соответствуют символы 01, появляющиеся на выходе кодера. Третий ИС также является 1, поэтому ему снова соответствует пунктирное ребро из узла с состоянием  в следующий узел с тем же состоянием
в следующий узел с тем же состоянием  (по горизонтали), которое обозначено 10, и эти же символы появляются на выходе кодера, как отклик кодера на третью информационную единицу. Четвертым ИС является 0 и поэтому ему соответствует ребро в виде сплошной линии, выходящей из узла с состоянием
(по горизонтали), которое обозначено 10, и эти же символы появляются на выходе кодера, как отклик кодера на третью информационную единицу. Четвертым ИС является 0 и поэтому ему соответствует ребро в виде сплошной линии, выходящей из узла с состоянием  , в узел с состоянием
, в узел с состоянием  и это ребро обозначено 01 и т. д.
и это ребро обозначено 01 и т. д.
С помощью решетчатой диаграммы по заданной ПКС нетрудно определить также ИС, которые явились причиной появления заданных кодовых символов. Так, если кодовая последовательность имеет вид 11 01 10 01 11 00, то соответствующей информационной последовательностью будет 111000. В этом случае соответствие между кодовыми и информационными символами устанавливаем по диаграмме, начиная с левого узла  .
.
Из узла  выходят два ребра, но только одно из них обозначено как 11 и т.к. это ребро пунктирное, то ему соответствует информационный символ 1. Из узла
выходят два ребра, но только одно из них обозначено как 11 и т.к. это ребро пунктирное, то ему соответствует информационный символ 1. Из узла  снова выходят два ребра, одно из них ребро 10, а другое ребро обозначено 01 и т.к. это ребро тоже пунктирное, то ему соответствует снова информационный символ 1 и т.д. В итоге получаем всю искомую последовательность информационных символов 111000.
снова выходят два ребра, одно из них ребро 10, а другое ребро обозначено 01 и т.к. это ребро тоже пунктирное, то ему соответствует снова информационный символ 1 и т.д. В итоге получаем всю искомую последовательность информационных символов 111000.
|
|
|
В 1967 г. Д.Форни обосновал применение решетчатых диаграмм, в том же году другой американский ученый А.Д.Витерби предложил новый метод декодирования сверточных кодов, основанный на использовании решетчатых диаграмм в виде достаточно простой итеративной процедуры, которая получила название «алгоритм Витерби» и успешно применяется на практике и в настоящее время.
Цель декодирования в случае использования сверточных кодов такая же, как и при использовании блочных кодов – исправить возможные ошибки при приеме кодовых символов, которые могут возникнуть на выходе демодулятора. Поэтому возникает вопрос о количестве исправляемых ошибок. Сколько ошибок может быть исправлено при декодировании свёрточного кода?
В случае блочного кода имелось в виду количество ошибок, которые могут произойти в пределах одной кодовой последовательности (одного блока), поэтому количество исправляемых ошибок определялось целым числом  , которое меньше, чем
, которое меньше, чем 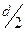 где
где  - кодовое расстояние.
- кодовое расстояние.
В случае сверточного кодирования нет блоков, поэтому необходимо:
1) ввести какую-то единицу длины, эквивалентную длине блока. При постановке вопроса о количестве исправляемых ошибок сверточным кодом нужно иметь в виду количество ошибок в пределах этой единицы длины;
2) определить для сверточных кодов такой важный параметр, как кодовое расстояние  (или параметр эквивалентный кодовому расстоянию), так как количество исправляемых ошибок определяется через величину этого параметра
(или параметр эквивалентный кодовому расстоянию), так как количество исправляемых ошибок определяется через величину этого параметра  .
.
Исследования сверточных кодов показали:
если интервал между ошибками составляет  символов или более, то при свёрточном декодировании каждая из этих ошибок исправляется независимо от другой ошибки, т.е. как одиночная ошибка;
символов или более, то при свёрточном декодировании каждая из этих ошибок исправляется независимо от другой ошибки, т.е. как одиночная ошибка;
если же интервал между двумя соседними ошибками меньше, чем 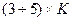 символов, то независимое исправление в общем случае уже невозможно, так как процесс исправления первой ошибки еще может не закончиться, а декодер приступит к исправлению второй ошибки, и на каком-то временном интервале одновременно исправляются обе ошибки (или большее число ошибок).
символов, то независимое исправление в общем случае уже невозможно, так как процесс исправления первой ошибки еще может не закончиться, а декодер приступит к исправлению второй ошибки, и на каком-то временном интервале одновременно исправляются обе ошибки (или большее число ошибок).
Таким образом, в случае сверточных кодов интервал протяженностью 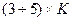 кодовых символов можно считать той условной единицей длины, которая эквивалентна длине блока в случае блочных кодов.
кодовых символов можно считать той условной единицей длины, которая эквивалентна длине блока в случае блочных кодов.
Напомним, что кодовое расстояние  в случае блочных кодов определялось, как минимальное расстояние между всевозможными парами кодовых последовательностей (блоков). Было установлено, что оно равно минимальному весу (минимальной норме) кодовой последовательности, отличной от нулевой кодовой последовательности. Эту величину можно также считать расстоянием Хемминга между нулевой последовательностью и кодовой последовательностью с минимальным весом.
в случае блочных кодов определялось, как минимальное расстояние между всевозможными парами кодовых последовательностей (блоков). Было установлено, что оно равно минимальному весу (минимальной норме) кодовой последовательности, отличной от нулевой кодовой последовательности. Эту величину можно также считать расстоянием Хемминга между нулевой последовательностью и кодовой последовательностью с минимальным весом.
Это свойство кодового расстояния для блочных кодов можно распространить и на сверточные коды. Кодовое расстояние  для сверточного кода можно определить как минимальное расстояние между всевозможными кодовыми последовательностями сверточного кода. Это расстояние
для сверточного кода можно определить как минимальное расстояние между всевозможными кодовыми последовательностями сверточного кода. Это расстояние  по аналогии с блочными кодами будет равно расстоянию Хемминга между нулевой кодовой последовательностью, которая получается на выходе сверточного кодера при приходе одних нулевых ИС, и кодовой последовательностью с минимальным весом, которая получается на выходе кодера, когда на его вход поступает одна информационная единица и только одни нули.
по аналогии с блочными кодами будет равно расстоянию Хемминга между нулевой кодовой последовательностью, которая получается на выходе сверточного кодера при приходе одних нулевых ИС, и кодовой последовательностью с минимальным весом, которая получается на выходе кодера, когда на его вход поступает одна информационная единица и только одни нули.
Эта последовательность ранее была получена и была названа «импульсной характеристикой сверточного кодера» (рис. 5). Можно найти отклик кодера на указанную последовательность 1000… также с помощью решетчатой диаграммы. Это будет та же самая последовательность 11 10 11 00 00…Расстояние Хемминга между этой кодовой последовательностью и нулевой кодовой последовательностью равна 5, т.е. кодовое расстояние для сверточного кода, порождаемым кодером на рис. 1, будет равно 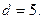


Для блочных кодов количество исправляемых ошибок  при декодировании
при декодировании  одного блока определялось неравенством
одного блока определялось неравенством  . Исследования сверточных кодов показали, что и для них количество исправляемых ошибок
. Исследования сверточных кодов показали, что и для них количество исправляемых ошибок  при декодировании должно удовлетворять тому же строгому неравенству
при декодировании должно удовлетворять тому же строгому неравенству
 (8).
(8).
Таким образом, если 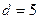 , то при сверточном декодировании можно исправить две ошибки, т.е.
, то при сверточном декодировании можно исправить две ошибки, т.е.  , так как
, так как 
В случае сверточных кодов вместо параметра  - кодового расстояния часто используют эквивалентный параметр
- кодового расстояния часто используют эквивалентный параметр  , который называется минимальным просветом или просто просветом. Более подробно об этом параметре будет изложено в дальнейшем.
, который называется минимальным просветом или просто просветом. Более подробно об этом параметре будет изложено в дальнейшем.
АЛГОРИТМ СВЕРТОЧНОГО ДЕКОДИРОВАНИЯ ВИТЕРБИ.
С целью реализации устойчивой работы кодера при сверточном декодировании периодически проводят очистку (промывку) регистра сдвига кодера от информационных символов путем подачи на кодер некоторого количества нулевых символов (не информационных). Эта операция называется периодическим отбрасыванием. Следующая партияинформационных символов поступает на кодер, когда все ячейки регистра сдвига находятся в нулевом состоянии, т.е. в состоянии  Обозначим:
Обозначим:
1)  - последовательность информационных символов, поступивших на вход кодера;
- последовательность информационных символов, поступивших на вход кодера;
2)  - последовательность кодовых символов с выхода кодера, которая передавалась по каналу;
- последовательность кодовых символов с выхода кодера, которая передавалась по каналу;
3)  - принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера.
- принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера.
С учетом сказанного рассмотрим алгоритм сверточного декодирования Витерби с использованием решетчатой диаграммы. Декодирование начинается в момент  (рис. 10). В результате очистки кодера между сообщениями будем считать, что декодер находится в начальном состоянии
(рис. 10). В результате очистки кодера между сообщениями будем считать, что декодер находится в начальном состоянии 
Предположим, что входная последовательность ИС на входе кодера
 = 0 0 0 0 0 0 (9),
= 0 0 0 0 0 0 (9),
от кодера по каналу связи передавалась кодовая последовательность (КП)
 00 00 00 00 00 00 (10),
00 00 00 00 00 00 (10),
состоящая из одних нулевых символов (можно было бы в качестве примера выбрать любую другую КП, но за последовательностью, состоящую из одних нулей, проще проследить по решетчатой диаграмме). Далее предположим, что в результате ошибок в демодуляторе на вход декодера вместо передаваемой кодовой последовательности (КП) (10) поступила последовательность  =10 00 10 00 00 00 (11),
=10 00 10 00 00 00 (11),
(т.е. ошибки произошли в тех разрядах, где стоят единицы).
На основании вышесказанного следует, расстояние между единицами в КП  меньше, чем
меньше, чем 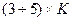 , где (
, где (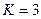 ), то каждую из этих ошибок нельзя считать одиночной ошибкой, независимой от другой ошибки и так как
), то каждую из этих ошибок нельзя считать одиночной ошибкой, независимой от другой ошибки и так как  , то эти две ошибки должны быть исправлены при использовании алгоритма свёрточного декодирования Витерби.
, то эти две ошибки должны быть исправлены при использовании алгоритма свёрточного декодирования Витерби.
На рис. 10 изображена решетчатая диаграмма декодера.

Рис. 10 Решетчатая диаграмма декодера
(степень кодирования  ).
).
Решетчатая диаграмма декодера на рис. 10 отличается от решетчатой диаграммы кодера на рис. 9 тем, что ребрам этих решеток соответствуют разные обозначения. Числа над ребрами решетки декодера определяются, как расстояния Хемминга между двумя символами принятой последовательности  , расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера (рис. 9).
, расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера (рис. 9).
Теперь изобразим отдельно ту часть решетчатой диаграммы декодера, которая расположена между моментами  и
и 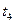 , для дальнейшего удобства обозначим буквами узлы на этой диаграмме.
, для дальнейшего удобства обозначим буквами узлы на этой диаграмме.

Рис. 11 Решетчатая диаграмма декодера между моментами  и
и 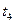 .
.
Определим по диаграмме на рис. 11 метрику путей по Хеммингу, исходящих из одной точки  и приходящих в узлы
и приходящих в узлы 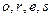 . Видим, что в узел
. Видим, что в узел  приходят два пути:
приходят два пути:  и
и  . Определим по диаграмме метрику этих путей:
. Определим по диаграмме метрику этих путей:

В узел  также приходят два пути:
также приходят два пути: 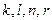 и
и 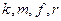 ; их метрики равны:
; их метрики равны:
 .
.
В узел  также приходят два пути:
также приходят два пути: 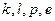 и
и  ; их метрики равны:
; их метрики равны:
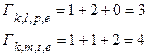 .
.
В узел  также приходят два пути;
также приходят два пути;  и
и  ; их метрики равны:
; их метрики равны:
 .
.
Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов 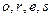 выжившим считается только один - тот путь, которому соответствует меньшая метрика. С учетом этого из двух путей, приходящих в узел
выжившим считается только один - тот путь, которому соответствует меньшая метрика. С учетом этого из двух путей, приходящих в узел  , выживет путь
, выживет путь  . Из остальных пар выживут соответственно
. Из остальных пар выживут соответственно 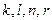 ,
, 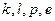 и
и  .
.
Снова построим диаграмму, но на ней укажем только выжившие пути к моменту 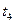 (рис. 12).
(рис. 12).

Рис. 12 Выжившие пути к моменту 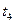 .
.
Теперь полученную диаграмму на рис. 12 достроим соответствующими ребрами до момента  (из каждого узла
(из каждого узла 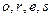 проводим два новых ребра).
проводим два новых ребра).
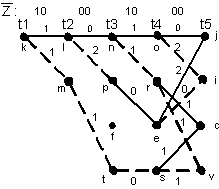
Рис. 13 Выжившие пути к моменту 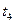 , достроенные до момента
, достроенные до момента  .
.
Над вновь достроенными ребрами (рис. 13) указываем расстояния Хемминга между двумя символами принятой последовательности  , расположенными над новыми ребрами, и соответствующими двумя символами на кодовой диаграмме (рис. 9), которыми отмечены эти новые ребра. Снова видим, что в узел
, расположенными над новыми ребрами, и соответствующими двумя символами на кодовой диаграмме (рис. 9), которыми отмечены эти новые ребра. Снова видим, что в узел  приходят два пути:
приходят два пути:  и
и 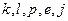 ; метрика этих путей равна:
; метрика этих путей равна:
 .
.
В узел  также приходят два пути:
также приходят два пути:  и
и  ; находим
; находим
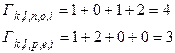 .
.
В узел  также приходят два пути:
также приходят два пути:  и
и  .
.
 .
.
В узел  также приходят пути:
также приходят пути:  и.
и.  .
.
 .
.
Аналогично вышесказанному из двух путей, приходящих в узел  выживает путь
выживает путь  ; из двух путей, приходящих в узел
; из двух путей, приходящих в узел  выживает путь
выживает путь  . Двум путям, приходящим в узел
. Двум путям, приходящим в узел  соответствуют одинаковые расстояния Хемминга, равные 3. Поэтому из этих двух путей произвольно выбираем любой, например:
соответствуют одинаковые расстояния Хемминга, равные 3. Поэтому из этих двух путей произвольно выбираем любой, например:  . Аналогично из двух путей, приходящих в узел
. Аналогично из двух путей, приходящих в узел  , произвольно выбираем путь
, произвольно выбираем путь  . Снова строим диаграмму от момента
. Снова строим диаграмму от момента  до момента
до момента  и на ней указываем только выжившие пути для момента
и на ней указываем только выжившие пути для момента  .
.

Рис. 14 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента 
Достраиваем полученную диаграмму соответствующими ребрами до момента  и указываем над вновь проведенными ребрами соответствующие расстояния Хемминга. Находим:
и указываем над вновь проведенными ребрами соответствующие расстояния Хемминга. Находим:




Согласно вышесказанному выживают такие пути:  строим на диаграмме эти пути (рис. 15).
строим на диаграмме эти пути (рис. 15).

Рис. 15 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента  .
.
Снова достраиваем полученную диаграмму соответствующими ребрами до момента  и указываем над вновь проведенными ребрами на рис. 15 соответствующие расстояния Хемминга. Находим:
и указываем над вновь проведенными ребрами на рис. 15 соответствующие расстояния Хемминга. Находим:
 .
.
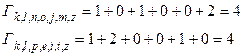

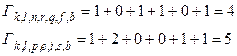
Выживают пути:  ;
;  ;
;  ;
;  .
.
Построим на диаграмме эти пути (рис. 16).

Рис. 16 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента  .
.
Снова достраиваем полученную диаграмму соответствующими ребрами до момента  и указываем над вновь проведенными ребрами на рис 16 соответствующие расстояния Хемминга. Находим:
и указываем над вновь проведенными ребрами на рис 16 соответствующие расстояния Хемминга. Находим:


 .
.

Выживают пути:  ;
;  ;
;  ;
;  ;
;
строим на диаграмме декодера эти пути (рис.17):
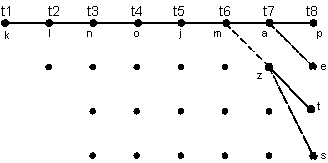
Рис. 17 Выжившие пути на решетчатой диаграмме декодера к моменту  .
.
Из построенной на рис. 17 диаграммы декодера видно, что от момента  до момента
до момента 
 выжил только один путь
выжил только один путь  . Теперь перенесем этот один выживший путь
. Теперь перенесем этот один выживший путь  с диаграммы декодера на диаграмму кодера, изображенную на рис. 9. Этому пути на диаграмме кодера (рис. 18) соответствуют обозначения ребер:
с диаграммы декодера на диаграмму кодера, изображенную на рис. 9. Этому пути на диаграмме кодера (рис. 18) соответствуют обозначения ребер:
00 00 00 00 00:

Рис. 18 Выживший путь  на диаграмме кодера.
на диаграмме кодера.
Декодер принимает решение, что на интервале от  до
до  по каналу передавалась последовательность кодовых символов, соответствующая выжившему пути
по каналу передавалась последовательность кодовых символов, соответствующая выжившему пути  т.е.:00 00 00 00 00. Эта последовательность совпадает с последовательностью:
т.е.:00 00 00 00 00. Эта последовательность совпадает с последовательностью:
 =00 00 00 00 00 от момента
=00 00 00 00 00 от момента  до
до  . Таким образом, ошибки, возникшие на выходе демодулятора, оказываются исправленными.
. Таким образом, ошибки, возникшие на выходе демодулятора, оказываются исправленными.
Из рассмотренного примера можно сделать следующие выводы:
1) При декодировании используются как решетчатая диаграмма кодера, так и решетчатая диаграмма декодера. Когда из демодулятора поступает пара принятых символов между моментами времени  и
и  , то определяются расстояния Хемминга между этой парой символов и парами символов, которыми отмечены ребра решетчатой диаграммы кодера между теми же моментами времени
, то определяются расстояния Хемминга между этой парой символов и парами символов, которыми отмечены ребра решетчатой диаграммы кодера между теми же моментами времени  и
и  , эти расстояния Хемминга пишут над соответствующими ребрами решетчатой диаграммы декодера. Обозначения (цифры) на ребрах решетки декодера накапливаются декодером в процессе декодирования.
, эти расстояния Хемминга пишут над соответствующими ребрами решетчатой диаграммы декодера. Обозначения (цифры) на ребрах решетки декодера накапливаются декодером в процессе декодирования.
Из сказанного следует, что решетчатая диаграмма кодера всегда одна и та же (она не зависит от принятой последовательности), а решетчатая диаграмма декодера определяется как диаграммой кодера, так и принятой последовательностью  , т.е. ее вид (значения цифр над ребрами) зависит от принятой последовательности
, т.е. ее вид (значения цифр над ребрами) зависит от принятой последовательности  .
.
2) С помощью пометок (цифр) на ребрах решетчатой диаграммы декодера для момента времени  определяются расстояния Хемминга между принятой последовательностью
определяются расстояния Хемминга между принятой последовательностью  и путями по диаграмме декодера. Все пути начинаются в точке
и путями по диаграмме декодера. Все пути начинаются в точке  (которой соответствует состояние
(которой соответствует состояние  ) и заканчиваются в узлах решетки декодера для момента
) и заканчиваются в узлах решетки декодера для момента  . Для каждого момента времени
. Для каждого момента времени  (где
(где  ) имеем четыре узла и в каждый узел приходят два пути (все они начинаются в одной той же точке
) имеем четыре узла и в каждый узел приходят два пути (все они начинаются в одной той же точке  ), т.е. всего путей будет 8, исходящих из точки
), т.е. всего путей будет 8, исходящих из точки  .
.
Декодирование Витерби состоит в том, что из двух путей, приходящих в один узел, при продолжении операции декодирования выживает только один – тот, которому соответствует меньшее расстояние Хемминга. Если эти два расстояния имеют одинаковую величину, то произвольно выбирается любой из двух.
Отсекание одного из двух путей, сходящихся в узле решетки, гарантирует, что число продолжающихся путей будет равно числу состояний (т.е. четырем для рассматриваемого кодера). В этом заключается существенное преимущество решетчатой диаграммы при сравнении с древовидной диаграммой при декодировании. Как отмечалось выше, при использовании древовидной диаграммы число возможных путей растет очень быстро – по закону 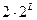 .
.
В результате использования алгоритма декодирования Витерби находится наиболее вероятный (с минимальным расстоянием Хемминга) путь через решетку декодера.
При определении этого пути происходит исправление ошибок, возникших при приеме передаваемой кодовой последовательности.
Как уже отмечалось, количество ошибок  , произошедших на интервале
, произошедших на интервале 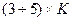 символов и исправляемых при сверточном декодировании, должно удовлетворять неравенству
символов и исправляемых при сверточном декодировании, должно удовлетворять неравенству  (см.(8)), где
(см.(8)), где  - кодовое расстояние. Величина
- кодовое расстояние. Величина  может быть определена как число единичных символов в импульсной характеристике свёрточного кодера.
может быть определена как число единичных символов в импульсной характеристике свёрточного кодера.
Эту же величину  можно определить как величину минимального просвета
можно определить как величину минимального просвета  или просто просвета. При этом имеет место равенство
или просто просвета. При этом имеет место равенство  .
.
Параметр  определяется с помощью решетчатой диаграммы декодера следующим образом:
определяется с помощью решетчатой диаграммы декодера следующим образом:
Предполагается, что по каналу передавалась нулевая последовательность
 =00 00 00 00 00 00 (12)
=00 00 00 00 00 00 (12)
и принятая последовательность 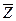 также нулевая, т.е.
также нулевая, т.е.
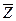 =00 00 00 00 00 00 (13)
=00 00 00 00 00 00 (13)
Для этой нулевой последовательности 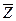 с помощью решетчатой диаграммы кодера строится решетчатая диаграмма декодера, представленная на рис. 19.
с помощью решетчатой диаграммы кодера строится решетчатая диаграмма декодера, представленная на рис. 19.
На диаграмме декодера (рис. 19) строятся всевозможные пути, которые расходятся из нулевого пути и снова возвращаются на нулевой путь в каком-то узле.

Рис. 19 Решетчатая диаграмма декодера последовательности 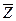 (13).
(13).
На рис 20 построены три пути, расходящиеся из нулевого пути в точке  и возвращающиеся на нулевой путь соответственно в точках
и возвращающиеся на нулевой путь соответственно в точках  . Эти пути обозначим:
. Эти пути обозначим:  .
.

Рис. 20 Решетчатая диаграмма декодера последовательности 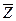
от момента  до момента
до момента  (13).
(13).
Из диаграммы рис. 20 можно определить метрику этих путей по Хеммингу:

На рис. 20 можно построить и другие аналогичные пути, но им будут соответствовать метрики большей величины. Минимальная величина из метрик таких путей называется минимальным просветом (или просто просветом) и обозначается  .
.
Таким образом, для рассматриваемого свёрточного кода (степень кодирования равна  ) величина просвета
) величина просвета  . Эта величина
. Эта величина  совпадает с величиной
совпадает с величиной  . для данного кода, которая определялась как число 1 (единиц) в импульсной характеристике кодера, т.е.
. для данного кода, которая определялась как число 1 (единиц) в импульсной характеристике кодера, т.е.  . Следовательно, величину просвета
. Следовательно, величину просвета  можно использовать также как и величину
можно использовать также как и величину  для определения количества исправляемых ошибок на интервале протяженностью
для определения количества исправляемых ошибок на интервале протяженностью 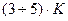 символов.
символов.
Рассмотрим еще один случай исправления комбинаций ошибок, характерный для ОФМ, когда две ошибки следуют друг за другом.
Пусть  = 00 00 00 00 00 00 00 (14),
= 00 00 00 00 00 00 00 (14),
 = 01 10 00 00 00 00 00 (15).
= 01 10 00 00 00 00 00 (15).
Как отмечено выше в последовательности (15) ошибкам соответствуют единичные символы. Пользуясь методикой построения решетчатых диаграмм предыдущего примера, строим диаграммы декодера рис. 21-рис. 29.

Рис. 21 Диаграмма декодера последовательности  (15).
(15).


Рис. 22 Выжившие пути к моменту 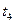 . Рис. 23 Выжившие пути к моменту
. Рис. 23 Выжившие пути к моменту 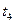 , достроенные до момента
, достроенные до момента  .
.
 ;
;  .
.
Выжившие пути на рис. 22 и рис. 23, а также на рис. 24  рис. 29 отмечены знаком
рис. 29 отмечены знаком  .
.


Рис. 24 Выжившие пути к моменту  ,
,
достроенные до момента  .
.

Рис. 25 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента  .
.




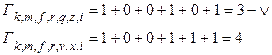




 Рис. 26 Выжившие пути к моменту
Рис. 26 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента  .
.


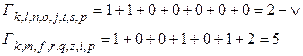





Рис. 27 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента  .
.



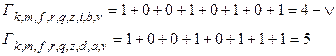


Рис. 28 Выжившие пути к моменту  , достроенные до момента
, достроенные до момента 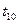 .
.


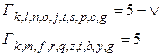
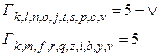
Строим на рис. 29 те пути, которые отмечены знаком  .
.
1. Для момента 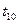 можно из 8-и путей оставить тот путь, метрика которого минимальна, (равна 2) т.к. метрика других путей существенно больше.
можно из 8-и путей оставить тот путь, метрика которого минимальна, (равна 2) т.к. метрика других путей существенно больше.
2. Если для момента 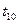 веса двух путей одинаковые, (например, равны 4), то лучше выбрать тот путь, которому соответствует меньший вес для момента
веса двух путей одинаковые, (например, равны 4), то лучше выбрать тот путь, которому соответствует меньший вес для момента  . Для момента
. Для момента  галочкой (
галочкой ( ) отмечен тот путь (рис. 27), для которого метрика
) отмечен тот путь (рис. 27), для которого метрика  равна 2.
равна 2.

Рис. 29 Выживший путь от момента  до момента
до момента  .
.
Из диаграммы рис. 29 можно сделать вывод, что от момента  до момента
до момента  выжил только один путь
выжил только один путь  . Перенесем этот выживший путь с диаграммы декодера на диаграмму кодера (рис. 9).
. Перенесем этот выживший путь с диаграммы декодера на диаграмму кодера (рис. 9).
Аналогично приведенному выше примеру по данным (9), (10), (11) декодер (рис. 29) принимает решение, что на интервале от момента  до момента
до момента  по каналу передавалась ПКС, соответствующая выжившему пути
по каналу передавалась ПКС, соответствующая выжившему пути  , т.е. 00 00 00 00 00 00 00 (рис. 9). Эта последовательность совпадает с последовательностью
, т.е. 00 00 00 00 00 00 00 (рис. 9). Эта последовательность совпадает с последовательностью  :00 00 00 00 00 00 00 (14) от момента
:00 00 00 00 00 00 00 (14) от момента  до момента
до момента  и ошибки, возникшие на выходе демодулятора, исправлены.
и ошибки, возникшие на выходе демодулятора, исправлены.
Главным критерием при выборе сверточного кода является требование, чтобы код не допускал катастрофического распространения ошибок и имел максимальный просвет при данной степени кодирования и длине кодового ограничения. Список наиболее известных кодов со степенью кодирования  , если
, если  имеют значения от 3 до 9, и со степенью кодирования
имеют значения от 3 до 9, и со степенью кодирования 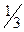 , если
, если  имеют значения от 3 до 8, приводится в таблице 3.
имеют значения от 3 до 8, приводится в таблице 3.
Таблица3.
|
|
|


