Задания по математике к экзамену, 1 курс 2-ой семестр

1. Из натуральных чисел от 1 до 18 учащийся наугад называет одно число. Какова вероятность того, что это число является делителем числа 18?

2. У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами

3. В среднем на 50 карманных фонариков приходится два неисправных. Найдите вероятность купить работающий фонарик.

4. Некто хочет купить стол, шкаф и диван. В магазине имеется три гарнитура, содержащих стол, шкаф и диван. 4 набора шкаф и диван,5 наборов стол и шкаф, 4 вида шкафов, 3 вида столов, 6 видов диванов. Сколькими способами может быть сделана покупка?

5. Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.

6. Игральный кубик подбрасывают один раз. Какова вероятность того, что выпавшее число окажется четным?

7. На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

8. Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по 10 каналам из сорока пяти показывают новости. Найдите вероятность того, что Маша попадет на канал, где новости не идут.

9. В ящике лежат 10 шариков, 3 из которых белые. Какова вероятность
того, что вынутый наугад шар окажется белым?

10. В группе 30 студентов. Сколькими способами можно выделить двоих дежурных, если старшего не должно быть?

11. В группе 30 студентов. Сколькими способами можно выделить двоих дежурных, если один из них должен быть старщим?

12. В ящике находятся 8 белых и 7 красных шариков. Последовательно вынимают два шарика. Какова вероятность того, что оба шарика белые?

13. Сколькими способами можно расставить на полке 5 книг разных авторов?

14. Какова вероятность того, что наугад выбранное двузначное число делится нацело на 11?

15. Игральный кубик подбрасывают один раз. Какова вероятность того, что выпавшее число окажется четным?

16. Какова вероятность того, что при подбрасывании игрального кубика выпадет количество очков, больше, чем 2?

17. В классе 25 учеников. Найдите количество способов выбрать из них двух дежурных.

18. Среди 9 платков, которые лежат в ящике, 2 платка белые. Наугад берут
один платок. Какова вероятность того, что он не белый?

19. Сколькими способами можно сформировать комиссию из 3 человек, которых нужно выбрать из 4 претендентов?

20. Сколько трехзначных чисел с разными цифрами можно записать, используя цифры 1, 2, 3, 4, 5, 6?

21. В коробке 12 зеленых и 8 синих шаров. Какова вероятность того, что наугад взятый шар окажется синим?

22. Сколько четырехзначных натуральных чисел с разными цифрами можно записать, используя цифры 0, 1, 2, 3?

23. Какова вероятность того, что наугад выбранное двузначное число делится нацело на 26?

24. В классной комнате 20 мальчиков и 5 девочек. Двое учащихся вышли один за другим из комнаты. Какова вероятность того, что учащиеся мальчики?

25. Из 4 студентов необходимо выбрать 2 для поездки за границу. Сколькими способами это можно сделать?

26. Игральный кубик подбросили один раз. Какова вероятность того, что выпало число, кратное 3?

27. Найдите медиану ряда 6; 4; 7; 8; 12; 4; 6; 7; 5.

28. Найдите медиану ряда 1, 12, 15, 17, 2, 8, 11, 7, 9.

29. Дан ряд чисел 16, 15, 18, 13, 12, 20, 16, 14, 11. Найдите на сколько мода этого ряда больше среднего.

30. Вычислите интеграл

31. Вычислите интеграл

32. Вычислить интеграл

33. Вычислить интеграл

34. Вычислите интеграл

35. Вычислите интеграл:

36. Вычислите интеграл

37. Вычислить интеграл

38. Найдите неопределенный интеграл .

39. Вычислите интеграл

40. Вычислить интеграл

41. Вычислите интеграл

42. Вычислите интеграл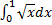

43. Найдите функции, имеющие производную

44. Найти все первообразные функции

45. Найдите все первообразные функции

46. Найдите все первообразные функции

47. Найти все первообразные функции

48. Для функции найдите первообразную, график которой
проходит через точку M(-1; 3).

49. Найдите площадь фигуры ограниченной линиями .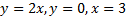

50. Найдите первообразную функции , график которой проходит через точку А(3;4).

51. Найдите первообразную функции , график которой проходит через точку А (-1; 2).

52. Найти площадь фигуры, ограниченной линиями

53. Найдите площадь фигуры, ограниченной осями координат, графиком функции и прямой .

54. Найдите площадь фигуры, ограниченной линями

55. Вычислите площадь фигуры, ограниченной параболой и прямой .

56. Найдите площадь фигуры, ограниченной графиком функции , прямыми x = -1, x = 2 и осью Oх

57. Найдите площадь фигуры, ограниченной графиком параболы , прямыми x= -2, x= -1 и осью Oх

58. Найдите площадь фигуры, ограниченной линиями

59. Найдите площадь фигуры, ограниченной линями

60. Найдите все первообразные функции

61. Найти общий вид первообразной функции

62. Найдите первообразную функции , график которой проходит через точку А (-1; 2)

63. Найти общий вид первообразной функции

64. Найдите первообразную функции график которой пересекает ось ординат в точке (0;3)

65. Найдите первообразную функции , график которой проходит через точку (0;3)

66. Найти площадь фигуры, ограниченной линиями

67. Найдите площадь фигуры ограниченной линями .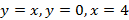

68. Найдите площадь фигуры, ограниченной линями

69. Вычислите площадь фигуры, ограниченной линиями и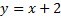

70. Найдите значение производной функции в точке .

71. Найдите производную функции

72. Найдите производную функции

73. Найдите производную функции

74. Найдите значение производной функции при .

75. Найдите производную функции в точке x₀= -1.

76. Найдите угловой коэффициент касательной к графику функци в
точке с абсциссой x₀ = 1.

77. Найдите угловой коэффициент касательной к графику функции в
точке с абсциссой x₀ = -1.

78. Для движущейся точки, скорость которой . Найдите значение скорости в момент, когда ускорение равно 12 м/с².

79. Для движущейся точки, скорость которой , найдите значение скорости в момент, когда ускорение равно 18 м/с².

80. Сколько критических точек имеет функция на промежутке

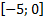
81. Решите неравенство , если .

82. Найдите наибольшее и наименьшее значение функции 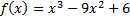на отрезке .

83. Найти наибольшее и наименьшее значение функции на отрезке

84. Найдите промежутки, на которых функция убывает.

85. Найти наибольшее и наименьшее значение функции на отрезке

86. Найдите наибольшее и наименьшее значение функции на отрезке .

87. Найти наименьшее значение функции на отрезке

88. Найдите промежутки возрастания функции

89. Найдите производную функции .

90. Найдите значение производной функции в точке х₀ = 3.

91. Найдите значение производной функции 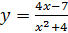в точке .

92. Найти промежутки монотонности функции

93. Найдите точку минимума функции

94. Найдите производную функции

95. Найдите , если .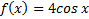

96. Решите неравенство , если

97. Найдите угловой коэффициент касательной, проведенной к графику функции в точке x₀=2.

98. Чему равно значение производной функции в точке х₀ = 2?

99. Найдите значение производной функции при х =16

100.Составить уравнение касательной к графику функции 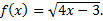в точке х₀ = 1.

101.Найти точки экстремума функции

102.Найдите точки экстремума функции

103.Найдите точки экстремума функции

104.Тело движется прямолинейно по закону 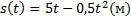, где t - время движения в секундах. Найдите скорость движения тела через 4 с после начала движения.

105.Тело движется по прямой так, что расстояние S от начальной точки изменяется по закону , где t-время движения в секундах. Найдите скорость тела через 3с после начала движения.

106.Найти критические точки функции: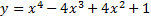

107.Найдите критические точки функции

108.Найдите промежутки возрастания функции

109.Исследуйте функцию и постройте ее график

110.Дана функция 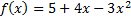. Найдите координаты точки ее графика, в котором угловой коэффициент касательной к нему равен -5.

111.Напишите уравнение касательной к графику функции в точке x₀= -2.

112.Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой

113.Найдите значение производной функции при .

114.В правильной треугольной призме длина диагонали боковой грани равна . При какой длине высот объем призмы будет наибольшим?

115.Найдите производную функции

116.Решите неравенство , если .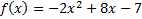

117.Решите уравнение:

118.Решите неравенство: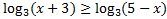

119.Решить неравенство:

120.Решите уравнение:

121.Решите уравнение: 49 ^х – 8 · 7 ^х + 7 = 0.

122.Решите уравнение: .

123.Решите уравнение

124.Решите уравнение:

125.Решите неравенство:

126.Решите уравнение:

127.Решите уравнение:

128.Решите уравнение: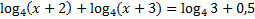

129.Решите неравенство: .

130.Решите уравнение: 3 · 16 ^х + 2 · 81 ^х = 5 · 36 ^х

131.Решите уравнение:

132.Решите уравнение:

133.Решите уравнение:

134.Решите неравенство:

135.Решите уравнение:

136.Решите уравнение: .

137.Решите уравнение:

138.Решите уравнение:

139.Решите неравенство:

140.Решите неравенство:

141.Решите неравенство:

142.Решите уравнение:

143.Решите неравенство:

144.Решите уравнение:

145.Решите неравенство: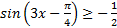

146.Решите уравнение:

147.Решите уравнение:

148.Решите неравенство:

149.Решите неравенство:

150.Решите уравнение:

151.Решите уравнение:

152.Решите неравенство:

153.Найдите сумму корней уравнения

154.Решите уравнение:

155.Решите уравнение:

156.Решите неравенство: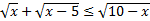

157.Решите уравнение: .

158.Решите неравенство:

159.Решите уравнение: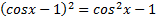

160.Решите уравнение:

161.Решите уравнение:

162.Образующая конуса равна 10 см, а радиус основания – 6 см. Найдитеобъем конуса.

163.Образующая конуса 16Ö3см и наклонена к плоскости основания под углом 60⁰. Найти высоту конуса.

164.Осевое сечение конуса прямоугольный треугольник. Найдите площадь боковой поверхности конуса, если радиус основания конуса равен 5 см.

165.Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости его основания под углом 60⁰. Найдите площадь боковой поверхности цилиндра.

166.Расстояние от центра основания конуса до образующей равно 3 см. Угол при вершине осевого сечения равен 120⁰. Найдите площадь осевого сечения конуса.

167.Расстояние от центра основания конуса до середины образующей равно6 см. Угол между образующей и плоскостью основания равен 60⁰. Найдите площадь осевого сечения конуса.

168.Вычислите площадь боковой поверхности конуса, осевым сечением которого является квадрат со стороной 8 см.

169.Площадь боковой поверхности конуса равна 136см², а его образующая равна 17 см. Найдите объем конуса.

170.Параллельно оси цилиндра проведено сечение, которое является квадратом со стороной 6 см и отсекает от окружности основания дугу, градусной мерой 60⁰. Найдите площадь боковой поверхности цилиндра.

171.Образующая конуса равна 13 см, а высота – 12 см. Найдите объем конуса.

172.Диагональ осевого сечения цилиндра равна d наклонена к плоскости основания под углом α. Найдите объем цилиндра.

173.Осевое сечение цилиндра – квадрат, периметр которого равен 64см. Найдите объем цилиндра.

174.Параллельно оси цилиндра проведено сечение, которое является квадратом и отсекает от окружности основания дугу, градусной мерой 90⁰. Найдите площадь боковой поверхности цилиндра, если радиус цилиндра 2Ö2равен см.

175.Высота конуса 12 см, а его образующая равна 13 см. найдите площадь боковой поверхности конуса.

176.Осевое сечение цилиндра – квадрат со стороной 6 см. Найдите объем цилиндра.

177.Расстояние от центра основания конуса до образующей равно 3 см. Угол при вершине осевого сечения равен 120⁰. Найдите площадь осевого сечения конуса.

178.Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна а. Эта хорда стягивает дугу, градусная ера которой равна 90°. Угол между образующими в сечении равен 60°. Найдите площадь боковой поверхности конуса.

179.Найдите объем тела, полученного при вращении прямоугольного треугольника с катетом 3см и прилежащим углом 30° вокруг меньшего катета.

180.Диагональ осевого сечения цилиндра равна 24Ö3 см и наклонена к плоскости его основания под углом 30⁰. Найдите площадь боковой поверхности цилиндра.

181.Параллельно оси цилиндра проведено сечение, которое является квадратом со стороной 6см и отсекает от окружности основания дугу, градусной мерой 90⁰. Найдите площадь боковой поверхности цилиндра.

182.В цилиндре параллельно его оси проведена плоскость, пересекающая нижнее основание цилиндра по хорде, которую видно из центра этого основания под углом α. Диагональ образовавшегося сечения наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности цилиндра, если площадь его основания равнаS.

183.Радиус основания цилиндра равен 4см, площадь боковой поверхности цилиндра вдвое больше площади основания.

184.Через две образующие конуса, угол между которыми равен φ, проведено сечение. Найдите площадь этого сечения, если высота конуса равна h, а угол между высотой и образующей конуса равен α

185.Через две образующиеся конуса, угол между которыми равен α, проведена плоскость, наклоненная к плоскости основания под углом β. Найдите объем конуса, если его образующая равна а

186.Угол между диагональю осевого сечения цилиндра и его образующей равен α. Найдите объем цилиндра, если диагональ осевого сечения равна d.

187.Из 1,1 м² листового железа изготовили цилиндрическую трубу диаметром 0,5 м. Найдите длину трубы.

188.Осевое сечение цилиндра – квадрат, диагональ которого равна 4см.Найдите объем цилиндра.

189.Образующая конуса равна 12см и составляет с плоскостью основания угол 30°. Найдите объем конуса.

190.Периметр равностороннего треугольника 27 см. некоторая точка равноудалена от вершин треугольника на 14 см. найдите расстояние от этой точки до плоскости треугольника.

191.Расстояние от точки М до сторон квадрата равно 13 см. найдите расстояние от точки М до плоскости квадрата, если сторона квадрата 10 см.

192.Из точки к плоскости проведены две наклонные, длины которых относятся как 5:6. Найдите расстояние от точки до плоскости, если соответствующие проекции наклонных равны 4 см и 3Ö3 см.

193.Дан DАВС. Плоскость, параллельная прямой АВ, пересекает сторону АС в точке К, а сторону ВС в точке М. Найдите АВ, если СК = 12 см, АС = 18 см, КМ = 36 см.

194.Через точку К, не лежащую между двумя параллельными плоскостями α и β, проведены две прямые, которые пересекают плоскость α в точках С₁ и С₂, а плоскость β − в точках D₁ и D₂ соответственно. Найдите С₁С₂, если D₁D₂=17 м, KC₁ = C₁D_{1 .}

195.Два луча с началом в точке А пересекают одну из параллельных плоскостей в точках А₁, В ₁, а другую в точках А₂, В₂. Вычислите АВ₁, если А₁В₁ = 4 см, А₂В ₂ = 16 см. Вычислить АВ₁, если А₁В1 = 4 см, А₂В₂ = 16 см, В₁В₂ = 15 см.

196.Через конец отрезка АВ проведена плоскость α, а через точку В и точку С отрезка АВ параллельные прямые, которые пересекают плоскость в точках В₁ и С₁. Найти ВВ₁, если АС = 3 см, АВ = 6 см, СС₁ = 4 с м.

197.Расстояние от точки M до сторон квадрата равно 13 см. Найдите расстояние от точки M до плоскости квадрата, если сторона квадрата равна 10 см.

198.Через концы отрезка АВ и его середину М проведены параллельные прямые, которые пересекают некоторую плоскость в точках А₁, В₁, М₁. Найдите длину отрезка ММ₁, если отрезок АВ не пересекает плоскость и АА₁ = 36 см, ВВ₁ = 48см.

199.Дан треугольник АВС и плоскость α, которая параллельна прямой АВ, пересекает АС в точке D, а сторону ВС – в точке К. Вычислите DK, если FD = 6,8см, DC = 4,3 см, FC = 8,6 см.

200.Три плоскости параллельны. Одна прямая пересекает их в точках А₁, А₂, А₃; другая – в точках В₁, В₂, В₃. Известно, что А₁А₂=4см, В₂В₃=9см, В₁В₂.=А₂А₃. Найдите длины отрезков А₁А₃ и В₁В₃.

201.Прямая а параллельна плоскости α. Через точки А и В прямой а проведены параллельные прямые пресекающие плоскость α в точках А₁ и В₁ соответственно. Найдите площадь четырехугольника АА₁ВВ₁ , если А₁В₁=13см, АВ₁=10см, ВВ₁=21см.

202.Точка О – центр квадрата со стороной 4 см. АО – прямая, перпендикулярная к плоскости квадрата, АО = 2Ö2 см. Вычислите расстояние от точки А до сторон квадрата.

203.Расстояние от точки M до всех вершин квадрата равно 5см. Найдите расстояние от точки M до плоскости квадрата, если диагональ квадрата равна 6см.

204.Точка К находится на расстоянии 2 см от плоскости α. Наклонные КА и КВ образуют соответственно с плоскостью α углы 45° и 30°, а угол между наклонными равен 135°. Найдите расстояние между точками.

205.Дан треугольник АВС и плоскость α, которая параллельна прямой АВ, пересекает АС в точке D, а сторону ВС – в точке К. Вычислите АВ, если DC = 8см, AC = 24 см, DK = 6 см.

206.Середина С отрезка АВ принадлежит плоскости α. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость α в точках А₁ и В₁. Длина отрезка А₁С равна 8см. Найдите длину отрезка А₁В₁

207.Стороны прямоугольника равны 9см и 12см. Из середины большей стороны восстановлен перпендикуляр длиной 4,8см к плоскости прямоугольника. Найти расстояние от конца этого перпендикуляра до одной из диагоналей

208.Диагонали ромба равны 12см и 16см. Точка М, расположенная вне плоскости ромба, удалена от всех сторон ромба на 8см. Найдите расстояние от точки М до плоскости ромба.

209.Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 4см. Отрезок СМ перпендикулярен плоскости треугольника и равен 2см. Найдите расстояние от точи М до прямой АВ.

210.Из точки к плоскости проведены перпендикуляр и наклонная, длина которой 20 см. Угол между наклонной и ее проекцией 60⁰. Найдите длину перпендикуляра.

211.ИЗ точки М к плоскости α проведены две наклонные MN и MК, длины которых относятся как 25:26. Найдите расстояние от точки М до плоскости α, если длины проекций наклонных MN и MК на эту плоскость равны 7см и 10см.

212.Отрезок АМ перпендикулярен к плоскости квадрата ABCD, угол ABM равен 30°. Найдите тангенс угла АСМ.

213.Сторона квадрата равна 4см. Точка, равноудалена от всех вершин квадрата, находится на расстоянии 6 см от точки пересечения диагоналей. Найдите расстояние от этой точки до вершин квадрата

214.В основании прямой призмы лежит ромб с большей диагональю равной 6Ö3см. Большая диагональ призмы образует с плоскостью основания угол 30⁰, а меньшая – угол 45⁰. Найдите объем призмы.

215.Сторона основания правильной треугольной пирамиды равна 6 см, а высота пирамиды - 5Ö3 см. Вычислите объём пирамиды.

216.В правильной треугольной пирамиде боковое ребро равно Ö37см. Найдите объем пирамиды, если радиус окружности, описанной около основания, равен 2Ö3см.

217.Сторона основания правильной четырехугольной пирамиды равна 8 см, а ее апофема – 10 см. Вычислите боковую поверхность пирамиды.

218.Основание пирамиды – прямоугольный треугольник с гипотенузой 18 см и острым углом 30⁰. Найдите объем пирамиды, если ее высота равна 6 см.

219.Вычислите объём пирамиды, в основании которой прямоугольный треугольник с катетами 9 см и 12 см, если высота пирамиды 18 см.

220.Основание прямой призмы – ромб с диагоналями 16см и 30см. Большая диагональ призмы равна 50см. Вычислите площадь полной поверхности призмы.

221.Сторона основания правильной четырехугольной призмы 5см, а боковое ребро 12 см. Вычислите объем призмы.

222.В правильной треугольной пирамиде радиус окружности, вписанной в основание, равен Ö3см. Апофема пирамиды равна 2Ö7см. Найдите объем пирамиды.

223.Высота правильной четырехугольной пирамиды 4 см. Найдите площадь боковой поверхности пирамиды, если двугранный угол при основании равен 45⁰.

224.Сторона основания правильной четырехугольной пирамиды 10 см, а двугранный угол при основании равен 60⁰. Найдите площадь полной поверхности.

225.В основании прямой призмы лежит ромб со стороной 6 см. Высота призмы равна 12 см. Найдите боковую поверхность призмы.

226.В основании прямой призмы лежит ромб с острым углом 60⁰ и стороной 6 см. Найдите меньшую диагональ призмы, если ее боковое ребро равно 8 см.

227.Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 13 см и катетом 5 см. Высота призмы равна радиусу окружности, вписанной в основание призмы. Найти объем призмы.

228.Найдите объем правильной четырехугольной пирамиды, сторона которой равна 6 см, диагональное сечение является равносторонним треугольником.

229.Объем треугольной пирамиды равен 75дм³. Высота пирамиды 5Ö3дм. Найдите площадь основания данной пирамиды.

230.В прямоугольном параллелепипеде ABCDA₁B₁C₁D ₁ AD=24см, CD=5см, AA₁=10см. Чему равна площадь прямоугольникаА₁В₁СD

231.Основание прямой призмы − прямоугольник со сторонами 6см и 8см. Боковое ребро 10см. Найдите объем призмы.

232.Сторона основания правильной четырехугольной пирамиды равна 4см, а боковая грань наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности пирамиды.

233.Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см. Высота призмы равна радиусу окружности, описанной около основания призмы. Найти объем призмы.

234.Ребро куба равно а. Определите расстояние от вершины куба до его диагонали.

235.Вычислите площадь боковой поверхности правильной четырехугольной призмы, диагональ которой равна см и наклонена к плоскости основания под углом 45°.

236.Основание прямой призмы –прямоугольный треугольник с гипотенузой 8 см и углом 30°. Объем призмы равен 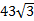см³. Найдите площадь боковой поверхности призмы.

237.Боковое ребро правильной четырехугольной пирамиды равно 8см и образует с плоскостью основания угол 60°. Найдите площадь боковой поверхности пирамиды.

238.Высота правильной четырехугольной пирамиды равна 15см, а апофема – 17см. Вычислите площадь боковой поверхности пирамиды.

239.В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ ребро АА₁ равно 10, а диагональ BD₁ равна 26. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A₁ и С.

240.Площадь сечения шара плоскостью равна 64π см². Радиус шара равен 17 см. Найдите расстояние от центра шара до плоскости сечения.

241.Плоскость проходит на расстоянии 8см от центра шара. Радиус сечения равен 15см. Найти площадь поверхности шара.

 

Поделиться:

Воспользуйтесь поиском по сайту: