 |
Анализ риска при формировании бюджета капиталовложений
|
|
|
|
Анализ риска важен при решении всех финансовых вопросов, особенно связанных с формированием бюджета капиталовложений. Как было показано в главе 3, чем выше риск, ассоциирующийся с какой-либо ценной бумагой, тем выше требуемая доходность для его компенсации. В равной мере это положение справедливо для инвестиционных проектов. Поскольку даже в рамках одной фирмы инвестиционные проекты могут широко отличаться друг от друга по степени рисковости, включение оценки риска в процесс принятия решения по бюджету капиталовложений имеет существенное значение. В данной главе будут обсуждены способы оценки и учета риска при разработке бюджета капиталовложений.
Введение в теорию риска, ассоциируемого с проектом
Можно выделить три четко различающихся типа риска: 1) единичный риск (stand-alone risk), когда риск проекта рассматривается изолированно, вне связи с другими проектами в портфеле фирмы; 2) внутрифирменный риск (within-firm risk), называемый также корпорационным риском, когда риск проекта рассматривается в его связи с портфелем проектов фирмы, и 3) рыночный риск (market risk), когда риск проекта рассматривается в контексте диверсификации капитала акционеров фирмы на фондовом рынке. Как мы увидим, доходы по конкретному проекту могут быть весьма неопределенными, значит, единичный риск такого проекта высок. Однако если взять в расчет диверсификацию, то принятие данного проекта к исполнению может не оказать большого влияния ни на корпорационный риск фирмы, ни на риск ее владельцев.
На рис. 9.1 приведена основная схема анализа рисковости проекта. Она будет обсуждена в этом разделе достаточно подробно, кроме того, в дальнейшем будет рассмотрен процесс количественной оценки различных рисков и их учета при принятии решения по бюджету капиталовложений. В связи с данным рисунком отметим следующие девять моментов.
|
|
|
1. Риск на рис. 9.1 и в данной главе в целом характеризует неопределенность будущих событий. При формировании бюджета капиталовложений под будущими событиями подразумевается будущая прибыльность проекта. Для некоторых проектов имеется возможность обработать статистические данные прошлых лет и проанализировать рисковость инвестиций. В частности, этот подход правомерен в ситуации, когда инвестиции связаны с решением о расширении. Например, если «Sears» планирует открыть новый магазин, «Citibank» — новый филиал, a GM — расширить производство автомобилей «шевроле», тогда опыт прошлого можно использовать в качестве отправной точки в оценке будущего риска. Аналогично компания, изучающая возможность вступления в новую сферу бизнеса, может получить представление о рисковости своих предполагаемых инвестиций, проанализировав статистические данные по уже существующим фирмам. Однако есть случаи, когда в отношении предполагаемых инвестиций невозможно получить статистические данные. Например, если бы GM

рассматривала проект производства электрических автомобилей, она не располагала бы большим объемом релевантной исторической информации для оценки рисковости проекта. Скорее GM положилась бы прежде всего на мнение своих руководителей, а они в свою очередь — на свой опыт в разработке, производстве и продаже новых изделий. Ниже будут приведены некоторые методики количественной оценки риска, вместе с тем с самого начала следует иметь в виду, что некоторые данные, используемые в анализе, неизбежно основываются на субъективных оценках, а не на устойчивых статистических наблюдениях.
2. В анализе риска используется целый ряд специфических терминов, определения которых приводятся ниже. Заметим, что эти термины и понятия взяты непосредственно из анализа портфельных инвестиций, рассмотренного в главах 2 и 3, поэтому в случае необходимости вернитесь снова к этим главам. Вот ключевые термины.
|
|
|
 — среднее квадратическое отклонение прибыльности рассматриваемого проекта, определяемое как среднее квадратическое отклонение внутренней доходности (IRR) проекта,
— среднее квадратическое отклонение прибыльности рассматриваемого проекта, определяемое как среднее квадратическое отклонение внутренней доходности (IRR) проекта,  — это показатель единичного риска проекта.
— это показатель единичного риска проекта.
 — коэффициент корреляции между доходностью анализируемого проекта и доходностью других активов фирмы. Рассчитывая его значение, пытаются выяснить следующее: будет ли данный проект прибыльным одновременно с другими активами фирмы, или его доходы, скорее всего, не будут зависеть от доходов по другим активам фирмы (или даже будут иметь обратную связь с ними)? Для некоторых проектов такую корреляцию можно определить по статистическим данным, но для большинства остальных она определяется на основе субъективной оценки.
— коэффициент корреляции между доходностью анализируемого проекта и доходностью других активов фирмы. Рассчитывая его значение, пытаются выяснить следующее: будет ли данный проект прибыльным одновременно с другими активами фирмы, или его доходы, скорее всего, не будут зависеть от доходов по другим активам фирмы (или даже будут иметь обратную связь с ними)? Для некоторых проектов такую корреляцию можно определить по статистическим данным, но для большинства остальных она определяется на основе субъективной оценки.
 — коэффициент корреляции между доходностью проекта и доходностью на фондовом рынке в среднем. Эта связь обычно оценивается на основе здравого смысла и субъективных экспертных оценок. Если значение коэффициента положительно, тогда проект при нормальной ситуации в экономике страны и на фондовом рынке также будет иметь тенденцию к высокой доходности.
— коэффициент корреляции между доходностью проекта и доходностью на фондовом рынке в среднем. Эта связь обычно оценивается на основе здравого смысла и субъективных экспертных оценок. Если значение коэффициента положительно, тогда проект при нормальной ситуации в экономике страны и на фондовом рынке также будет иметь тенденцию к высокой доходности.
 — среднее квадратическое отклонение доходности активов фирмы до принятия к исполнению рассматриваемого проекта. Она определяется как (чистый доход + амортизация + процент): (заемные средства + собственный капитал). Заметьте, что средняя доходность фирмы есть, в сущности, что-то вроде средней IRR по прежним проектам. Если
— среднее квадратическое отклонение доходности активов фирмы до принятия к исполнению рассматриваемого проекта. Она определяется как (чистый доход + амортизация + процент): (заемные средства + собственный капитал). Заметьте, что средняя доходность фирмы есть, в сущности, что-то вроде средней IRR по прежним проектам. Если  невелика, фирма стабильна и ее корпорационный риск относительно низок. Если же
невелика, фирма стабильна и ее корпорационный риск относительно низок. Если же  велика, степень корпорационного риска фирмы высока и ее шансы стать банкротом выше, чем в случае, когда
велика, степень корпорационного риска фирмы высока и ее шансы стать банкротом выше, чем в случае, когда  мала. Значение
мала. Значение  за прошедшие годы может быть определено статистически. Однако изменения в финансовом положении фирмы могут сделать ожидаемый будущий корпорационный риск отличным от прежнего риска. В этом случае в анализе предпочтительнее использовать субъективную оценку
за прошедшие годы может быть определено статистически. Однако изменения в финансовом положении фирмы могут сделать ожидаемый будущий корпорационный риск отличным от прежнего риска. В этом случае в анализе предпочтительнее использовать субъективную оценку  .
.
 — среднее квадратическое отклонение рыночной доходности. Эта величина определяется на основе данных прошлых лет и составляет примерно 15%.
— среднее квадратическое отклонение рыночной доходности. Эта величина определяется на основе данных прошлых лет и составляет примерно 15%.
|
|
|
 — внутрифирменный
— внутрифирменный  -коэффициент. Определяется (концептуально) путем регрессии доходности проекта относительно доходности фирмы без учета данного проекта. Если представить себе проект как акцию, а фирму как рынок, тогда
-коэффициент. Определяется (концептуально) путем регрессии доходности проекта относительно доходности фирмы без учета данного проекта. Если представить себе проект как акцию, а фирму как рынок, тогда  определяется аналогично тому, как определялись
определяется аналогично тому, как определялись  -коэффициенты акций в главе 3. Заметим также, что для расчета внутрифирменного
-коэффициенты акций в главе 3. Заметим также, что для расчета внутрифирменного  -коэффициента можно воспользоваться следующей формулой, выведенной в главе 3:
-коэффициента можно воспользоваться следующей формулой, выведенной в главе 3:
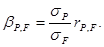
Отсюда видно, что внутрифирменный  -коэффициент проекта есть функция его единичного риска,
-коэффициент проекта есть функция его единичного риска,  , рисковости других активов фирмы,
, рисковости других активов фирмы,  , и коэффициента корреляции между доходами по проекту и доходами от других активов фирмы. Таким образом, внутрифирменная
, и коэффициента корреляции между доходами по проекту и доходами от других активов фирмы. Таким образом, внутрифирменная  является мерой вклада проекта в корпорационный риск фирмы точно так же, как
является мерой вклада проекта в корпорационный риск фирмы точно так же, как  акции есть мера ее вклада в риск, с которым сталкивается хорошо диверсифицированный инвестор — держатель большого портфеля акций.
акции есть мера ее вклада в риск, с которым сталкивается хорошо диверсифицированный инвестор — держатель большого портфеля акций.
 —
—  -коэффициент проекта в контексте рыночного портфеля акций; может быть рассчитан (теоретически) путем регрессии доходности проекта относительно доходности на рынке.
-коэффициент проекта в контексте рыночного портфеля акций; может быть рассчитан (теоретически) путем регрессии доходности проекта относительно доходности на рынке.  можно выразить формулой, аналогичной формуле для
можно выразить формулой, аналогичной формуле для  . Это рыночная
. Это рыночная  проекта. Она является мерой вклада проекта в риск, которому подвергаются акционеры фирмы, предположительно являющиеся держателями хорошо диверсифицированного портфеля.
проекта. Она является мерой вклада проекта в риск, которому подвергаются акционеры фирмы, предположительно являющиеся держателями хорошо диверсифицированного портфеля.
3. Внимательно посмотрите на рис. 9.1. Верхний прямоугольник показывает, что у риска проекта имеется три характеристики: 1) среднее квадратическое отклонение прогнозируемых значений доходности проекта,  ; 2) корреляция доходности проекта с доходностью других активов фирмы,
; 2) корреляция доходности проекта с доходностью других активов фирмы,  , и 3) корреляция доходности проекта с доходностью фондового рынка,
, и 3) корреляция доходности проекта с доходностью фондового рынка,  . Как показано в прямоугольнике слева, две характеристики риска проекта —
. Как показано в прямоугольнике слева, две характеристики риска проекта —  и
и  — в сочетании со средним квадратическим отклонением доходности по другим активам фирмы,
— в сочетании со средним квадратическим отклонением доходности по другим активам фирмы,  , определяют вклад проекта в корпорационный риск фирмы, или внутрифирменный риск. В прямоугольнике справа показано, что две характеристики риска проекта —
, определяют вклад проекта в корпорационный риск фирмы, или внутрифирменный риск. В прямоугольнике справа показано, что две характеристики риска проекта —  и
и  — в сочетании с рисковостью рынка,
— в сочетании с рисковостью рынка,  , определяют вклад проекта в рисковость портфеля хорошо диверсифицированного инвестора, или в рыночный риск проекта.
, определяют вклад проекта в рисковость портфеля хорошо диверсифицированного инвестора, или в рыночный риск проекта.
|
|
|
4. Очевидно, что, оценивая рисковость проекта, особенно важно измерить его единичный риск,  , так как при формировании бюджета капиталовложений эта составляющая используется на всех этапах анализа в зависимости от того, что хотят измерить: корпорационный риск, рыночный риск или оба вида риска.
, так как при формировании бюджета капиталовложений эта составляющая используется на всех этапах анализа в зависимости от того, что хотят измерить: корпорационный риск, рыночный риск или оба вида риска.
5. Большинство проектов имеет положительный коэффициент корреляции с другими активами фирмы, причем его значение наиболее высоко для проектов, которые относятся к профилирующей области деятельности фирмы, и менее высоко (но все-таки положительно) для проектов, выходящих за рамки профилирующей области. Тем не менее коэффициент корреляции редко равен +1.0. В таком случае некоторая часть единичного риска большинства проектов с помощью диверсификации будет устранена, и чем больше фирма, тем этот эффект вероятнее. Поэтому на графике распределения вероятностей в левом нижнем углу рис. 9.1 для единичного риска, выбранного для иллюстрации проекта, кривая распределения показана более плоской, чем для риска этого проекта с точки зрения портфеля активов фирмы. Это говорит о том, что внутрифирменной риск проекта меньше, чем его единичный риск.
6. Большинство проектов, кроме того, положительно коррелирует с другими активами в экономике страны — большая часть ценных бумаг корпораций высокодоходна в условиях экономического роста, и наоборот. Однако связь, как правило, не является функциональной, поэтому единичный риск типичного проекта также выше, чем его рыночный риск. Следовательно, приведенная на правом графике кривая распределения вероятностей для единичного риска проекта является более плоской, чем для распределения риска в контексте рыночного портфеля.
7. Если внутрифирменная  проекта равна 1.0, тогда степень корпо-эационного риска проекта равна степени риска среднего проекта. Если
проекта равна 1.0, тогда степень корпо-эационного риска проекта равна степени риска среднего проекта. Если  больше 1.0, риск проекта больше среднего корпорационного риска, если
больше 1.0, риск проекта больше среднего корпорационного риска, если  меньше 1.0, имеет место обратное. Риск, превышающий средний корпорационный, приводит, как правило, к использованию средневзвешенной цены капитала (WACC) выше средней. Однако точной формулы для определения того, каким должно быть превышение, нет, поэтому величина поправки — вопрос здравого смысла.
меньше 1.0, имеет место обратное. Риск, превышающий средний корпорационный, приводит, как правило, к использованию средневзвешенной цены капитала (WACC) выше средней. Однако точной формулы для определения того, каким должно быть превышение, нет, поэтому величина поправки — вопрос здравого смысла.
8. Если рыночная  проекта,
проекта,  , равна рыночной
, равна рыночной  фирмы, тогда проект имеет ту же степень рыночного риска, что и средний проект. Если
фирмы, тогда проект имеет ту же степень рыночного риска, что и средний проект. Если  больше
больше  фирмы, тогда риск проекта больше среднего рыночного риска, и наоборот. Рыночная
фирмы, тогда риск проекта больше среднего рыночного риска, и наоборот. Рыночная  проекта выше средней (под средней подразумевается
проекта выше средней (под средней подразумевается  фирмы) приводит, как правило, к повышению WACC. Для внесения поправки можно воспользоваться моделью оценки доходности финансовых активов (САРМ). Процесс внесения поправки будет рассмотрен в данной главе.
фирмы) приводит, как правило, к повышению WACC. Для внесения поправки можно воспользоваться моделью оценки доходности финансовых активов (САРМ). Процесс внесения поправки будет рассмотрен в данной главе.
|
|
|
9. Иногда высказываются утверждения, что единичный или корпорационный риски в том смысле, в каком они здесь определены, не имеют значения. Если фирма стремится к максимизации богатства акционеров, единственным релевантным риском является рыночный риск. Такая позиция некорректна по следующим причинам.
а. Недиверсифицированные акционеры, включая владельцев мелких предприятий, больше озабочены корпорационным риском, чем рыночным.
б. Многие теоретики в области финансов утверждают, что инвесторы, даже хорошо диверсифицированные, определяя требуемую доходность, кроме рыночного риска принимают во внимание и другие факторы. Один из таких факторов — риск финансового спада, который зависит от корпорационного риска фирмы. Эмпирические исследования факторов требуемой доходности, как правило, приводят к заключению о важности как рыночного, так и корпорационного риска.
в. Стабильность фирмы имеет значение для всех остальных причастных к ее деятельности контрагентов, включая ее менеджеров, работников, клиентов, поставщиков, кредиторов, представителей социальной сферы. Фирмы, находящиеся под угрозой банкротства или снижения прибылей и объемов производства, испытывают трудности в привлечении и удержании у себя хороших менеджеров и рабочих. Кроме того, со слабыми фирмами не склонны иметь дело как поставщики, так и клиенты. Таким фирмам трудно получить заем иначе, как под высокие проценты. Эти факторы ведут к снижению прибыльности рисковых фирм и, следовательно, цены их акций.
По указанным причинам корпорационный риск важен даже для хорошо диверсифицированных акционеров.
Вопросы для самопроверки
Назовите три вида риска проекта. Что является мерой каждого из них? Каким образом эти три вида риска связаны между собой?
Почему менеджерам следует анализировать не только рыночный, но и корпорационный риск проекта?
Единичный риск
Единичный риск проекта сам по себе не представляет большого интереса. Он релевантен только в отношении некоммерческих (неакционерных) фирм с одним проектом или для однопроектных фирм с недиверсифицированными акционерами. Тем не менее, как было показано выше, единичный риск - это важный фактор (вместе с коэффициентами корреляции) как внутрифирменного, так и рыночного риска. Поэтому на оценку единичного риска фирмы тратят много времени и усилий.
Анализ единичного риска проекта начинается с установления неопределенности, присущей денежным потокам проекта. Есть ряд путей для проведения такого анализа: от простого высказывания мнений до сложных экономических и статистических исследований с привлечением компьютерных моделей. Для иллюстрации процесса вернемся к проекту разработки компьютера для оросительной системы компании «Robert Irwin» (RIC), который обсуждался в главе 8. Большинство отдельных денежных потоков в табл. 8.3-8.5, которые в результате давали ожидаемый чистый денежный поток проекта, показанный в табл. 8.6, могут считаться неопределенными. Например, прогнозируемый сбыт на 1996 г. составил 25000 единиц продукции по нетто-цене 2200 дол. за штуку, или всего 55 млн. дол. Однако объем реализации в единицах почти наверняка будет несколько выше или ниже 25000, а продажная цена, вероятно, будет отличаться от 2200 дол. В сущности оценки объема сбыта и цены — это действительно ожидаемые величины, взятые из распределений вероятности, так же как и многие другие величины, приведенные в табл. 8.3-8.5. Кривые распределений могут быть относительно «острыми», отражая малость значений дисперсии и риска, или «плоскими», указывая на большую степень неопределенности рассматриваемой переменной и, следовательно, на большую степень единичного риска.
Характер распределений отдельных денежных потоков и их корреляция друг с другом определяют характер распределений NPV и IRR проекта и, таким образом, его единичный риск. В последующих разделах будут изложены четыре метода оценки единичного риска проекта: 1) анализ чувствительности, 2) анализ сценариев, 3) имитационное моделирование методом Монте-Карло и 4) анализ дерева решений.
Анализ чувствительности
На интуитивном уровне понятно, что многие переменные, определяющие денежные потоки проекта, не известны наверняка, а скорее подчиняются некоторому закону распределения вероятностей. Известно также, что если ключевая переменная, например объем проданной продукции, меняется, меняются и NPV и IRR проекта. Анализ чувствительности (sensitivity analysis) — это метод, точно показывающий, насколько изменятся NPV и IRR в ответ на данное изменение одной входной переменной при том, что все остальные условия не меняются.
Анализ чувствительности начинается с построения базового варианта, разработанного на основе ожидаемых значений входных величин. Для примера рассмотрим данные, приведенные в табл. 8.4. В таблицу сведены прогнозные значения показателей денежных потоков для проекта компьютерного управления оросительной системой фирмы RIC. Значения объема сбыта, себестоимости реализованной продукции, постоянных и переменных затрат — ожидаемые, или базовые, значения, а приведенный в табл. 8.6 NPV 12075384 дол. называется NPV базового варианта. Теперь зададим серию вопросов «что если?». Что если объем сбыта в натуральных единицах упадет по сравнению с ожидаемым уровнем на 20%? Что если упадет себестоимость единицы реализованной продукции? Что если переменные затраты составят 70% объема сбыта в стоимостном выражении, а не ожидаемые 65%? Анализ чувствительности разработан для того, чтобы снабдить ответами на подобные вопросы лицо, принимающее решение.
Выполняя анализ чувствительности, обычно неоднократно меняют каждую переменную, в определенной пропорции увеличивая или уменьшая ее ожидаемое значение и оставляя другие факторы постоянными. Всякий раз рассчитываются значения NPV, и, наконец, на их основе строится график зависимости NPV от изменяемой переменной. На рис. 9.2 показаны графики чувствительности компьютерного проекта для трех ключевых входных переменных. Таблица под графиками содержит значения NPV, которые использовались для их построения. Наклон линий регрессии показывает, насколько чувствителен NPV проекта к изменениям на каждом входе: чем круче наклон, тем чувствительнее NPV к изменению переменной. Видно, что NPV проекта очень чувствителен к изменению переменных затрат, довольно чувствителен к изменению объема сбыта и относительно нечувствителен к изменению цены капитала.
В сравнительном анализе проект с более крутыми кривыми чувствительности считается более рисковым, поскольку сравнительно небольшая ошибка в оценке переменной, например переменных затрат на единицу продукции, дает большую ошибку в прогнозируемой NPV проекта. Таким образом, анализ чувствительности может помочь проникнуть в суть рисковости проекта.

Прежде чем двигаться дальше, обратим внимание на два следующих дополнительных замечания по поводу анализа чувствительности. Во-первых, для выполнения анализа чувствительности идеально подходят компьютерные модели в среде электронных таблиц, поскольку такие модели автоматически пересчитывают NPV при изменении какой-либо входной величины. Так, для проведения анализа, результаты которого представлены на рис. 9.2, был использован пакет Lotus 1-2-3. Во-вторых, можно представить все кривые чувствительности на одном графике. Это облегчает непосредственное сравнение чувствительности для разных входных переменных.
Анализ сценариев
Несмотря на то что анализ чувствительности, возможно, наиболее широко применяемый метод анализа риска, он все-таки имеет ряд ограничений. Рассмотрим, например, проект о разработке угольной шахты, NPV которого резко меняется при изменении объема добычи и цены реализации. Однако если заключен контракт на продажу фиксированного количества угля по фиксированной цене за тонну с учетом инфляции, тогда угледобывающее предприятие может быть достаточно благополучным, несмотря на крутизну своих кривых чувствительности. Как правило, единичный риск проекта зависит: 1) от чувствителъности его NPV к изменениям ключевых переменных и 2) от диапазона вероятных значений этих переменных, что отражается в их распределениях вероятностей. Поскольку анализ чувствительности рассматривает только первый фактор, он неполон.
Метод анализа риска, который рассматривает как чувствительность NPV к изменениям ключевых переменных, так и диапазон вероятных значений переменных, — это анализ сценариев. При этом финансовый аналитик просит менеджера-практика выбрать «плохую» совокупность условий (низкий объем реализации в натуральных единицах, низкая цена реализации, высокие переменные затраты на единицу продукции, большая стоимость строительства и т. д.), среднюю, или «наиболее вероятную», совокупность и «хорошую» совокупность. Затем рассчитываются NPV в «плохих» и «хороших» условиях и сравниваются с «наиболее вероятным» NPV.
Для примера вернемся к проекту о производстве компьютеров оросительной системы. Допустим, менеджеры RIC вполне уверены в своих оценках всех переменных денежных потоков проекта, за исключением цены и объема реализации. Далее, предположим, что они считают совершенно невероятным падение объема реализации ниже 15000 или его повышение сверх 35000 ед. Аналогично они ожидают, что установленная на рынке цена реализации может варьировать в пределах от 1700 до 2700 дол. Таким образом, 15000 ед. продукции по цене 1700 дол. определяют нижнюю границу, или наихудший сценарий, а 35000 ед. продукции по цене 2700 дол. — верхнюю границу, или наилучший сценарий. Напомним, что наиболее вероятные значения, характеризующие базовый вариант, — это 25 000 ед. продукции по цене 2200 дол. Поскольку эта цена относится к 1996 г., в дальнейшем возможен ее рост ввиду инфляции.
Анализ сценариев предполагает расчет NPV по каждому из трех возможных вариантов — наихудшему, наилучшему и наиболее вероятному.1 Результаты анализа
Таблица 9.1
Анализ сценариев
| Сценарий | Объем реализации, ед. | Цена реализации, дол. | NPV, тыс. дол. | Вероятность | Результат |
| 4-5 = 6 | |||||
| Наихудший Наиболее вероятный Наилучший | -10079 12075 | 0.25 0.50 0.25 | -2520 | ||
| Ожидаемый NPV | |||||
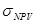 18421 18421
|
Примечание. Значения других переменных (кроме объема реализации и цены) даны в прогнозных оценках.
с помощью пакета Lotus сведены в табл. 9.1. Видно, что наиболее вероятная ситуация прогнозирует положительный NPV; наихудшая ситуация дает отрицательный NPV, а наилучшая ситуация ведет к очень большому положительному NPV. Далее можно рассчитать ожидаемое значение NPV, среднее квадратическое отклонение и коэффициент вариации. Для этого необходимо оценить вероятность осуществления каждого сценария. Предположим, руководство считает, что вероятность возникновения наихудшей ситуации равна 25%. наиболее вероятной — 50% и наилучшей — 25%. Разумеется, точно оценить вероятность осуществления сценариев очень трудно.
Табл. 9.1 содержит дискретное распределение вероятностей доходов, аналогичное описанному в главе 2, за исключением выражения доходов не в процентах (доходность), а в долларах (NPV). Ожидаемое значение NPV (в тыс. дол.):
0.25(-10 079) + 0.50 • 12 075 + 0.25 • 41 752 = 13 956.
Полученное значение отличается от NPV базового варианта. Это объясняется тем, что две исходные переменные, объем реализации и цена, варьируют неодинаково — большая вариация первой переменной приводит к сдвигу ожидаемого NPV в сторону увеличения. Среднее квадратическое отклонение NPV (в тыс. дол.):2

Наконец, коэффициент вариации NPV проекта равен 1.3:

Для того чтобы получить представление об относительной корпорационной рисковости проекта, можно сравнить коэффициенты вариации NPV нового и среднего проекта RIC. Существующие активы RIC имеют совокупный коэффициент вариации, равный приблизительно 1.0. Таким образом, на основании этого показателя единичного общего риска можно сделать вывод, что проект компьютерного управления оросительной системой более рисковый, чем средний проект фирмы.
Хотя анализ сценариев дает полезную информацию о единичном риске проекта, тем не менее он ограничен рассмотрением только нескольких дискретных исходов проекта, в то время как в действительности существует бесконечное число возможностей. В следующем разделе будет описан метод оценки единичного риска проекта, позволяющий в известной степени преодолеть эту проблему.
Имитационное моделирование методом Монте-Карло
Этот метод обязан своим названием городу, известному игорными домами. Он объединяет анализ чувствительности и анализ распределений вероятностей входных переменных.3 Однако моделирование требует относительно мощной системы
программного обеспечения, в то время как анализ сценариев можно провести на компьютере в среде электронных таблиц или даже с помощью калькулятора.
Первый этап компьютерного моделирования состоит в задании распределения вероятностей каждой исходной переменной денежного потока, например цены и объема реализации. Для этой цели обычно используют непрерывные распределения, полностью задаваемые небольшим числом параметров, например среднее и среднее квадратическое отклонение или нижний предел, наиболее вероятное значение и верхний предел варьирующего признака. Собственно процесс моделирования выполняется следующим образом.
1. Программа моделирования случайным образом выбирает значение для каждой исходной переменной, основываясь на ее заданном распределении вероятностей. Например, выбирается значение объема реализации в натуральных единицах.
2. Значение, выбранное для каждой варьируемой переменной, вместе с заданными значениями других факторов, таких как ставка налога и амортизационные отчисления, затем используется в модели для определения чистых денежных потоков по каждому году. Далее рассчитывается NPV проекта в данном конкретном компьютерном прогоне.
3. Этапы 1 и 2 многократно повторяются, скажем 1000 раз, что даст 1000 NPV, которые составят распределение вероятностей; тем самым получают ожидаемые значения NPV и среднего квадратического отклонения.
Пользуясь этой процедурой, можно выполнить имитационный анализ проекта RIC. Как и в анализе сценариев, мы упростили пример, задав распределения только для двух ключевых переменных — объема и цены реализации. Для всех остальных переменных указаны лишь их ожидаемые значения.
Предполагается, что цена реализации может быть представлена с помощью непрерывного нормального распределения, при этом ожидаемое значение равняется 2200 дол., а действительная цена реализации вряд ли отклонится от ожидаемого значения больше чем на 500 дол., т. е. упадет ниже 1700 дол. или поднимется выше 2700 дол. Как известно, в случае нормального распределения большая часть значений переменной отклоняется от среднего не более чем на  . Таким образом, в качестве обоснованного допущения принимается среднее квадратическое отклонение цены реализации, равное 500 дол.: 3 ≈ 167 дол., а в компьютер вводится информация, что распределение цены реализации нормально, причем ожидаемое значение равно 2200 дол., а среднее квадратическое отклонение — 167 дол.
. Таким образом, в качестве обоснованного допущения принимается среднее квадратическое отклонение цены реализации, равное 500 дол.: 3 ≈ 167 дол., а в компьютер вводится информация, что распределение цены реализации нормально, причем ожидаемое значение равно 2200 дол., а среднее квадратическое отклонение — 167 дол.
Далее, делается допущение, что прогнозируемое распределение объема реализации (в натуральных единицах) также симметрично, а ожидаемое значение составляет 25000 ед. При устойчивом спросе и имеющихся производственных мощностях реализация может достичь 40000 ед. Однако если товар не будет пользоваться спросом, реализация может снизиться до 10000 ед. Вновь можно было бы задать нормальное распределение, но в случае объема реализации наиболее подходящим, по нашему мнению, будет треугольное распределение с наиболее вероятным (и ожидаемым) значением 25000, нижним пределом 10000 и верхним пределом 40000.
В процессе моделирования указанные данные обработаны с помощью встроенной в пакет Lotus программы @RISK. Результаты вычислений сведены в Табл. 9.2, а диаграмма смоделированного распределения вероятностей NPV при ведена на рис. 9.3. Вероятность того, что NPV превысит —2114000 дол., равна 90%. Следовательно, есть 10%-нал вероятность того, что NPV будет равен или меньше —2114000 дол. Имеется примерно 14%-ная возможность отрицательного NPV проекта, т. е. 86%-ная вероятность того, что NPV будет больше нуля. В результате вычислений получены также ожидаемое (среднее) значение и среднее квадратическое отклонение NPV. Итак, можно рассчитать коэффициент вариации NPV проекта и оценить единичный риск проекта так же, как это было проделано при рассмотрении анализа сценариев.4
Несмотря на очевидную привлекательность, имитационный анализ не используется в промышленности так широко, как этого можно было бы ожидать. Одна из главных трудностей состоит в обосновании распределений вероятностей переменных и корреляций между ними. Механически включить в имитационный анализ любой тип корреляции между переменными не составляет большого труда. Например, @RISK позволяет задать как пространственную, так и динамическую корреляцию. Тем не менее определить, какими должны быть корреляции, непросто. Действительно, эксперты, пытавшиеся получить информацию о таких взаимосвязях у менеджеров-практиков в виде конкретных оценок, отмечали сопряженные с этим трудности. Безусловно, проблема не является непреодолимой, и моделирование используется в бизнесе все чаще и чаще. Тем не менее важно иметь в виду трудность получения достоверных оценок вероятностных распределений переменных и корреляций между распределениями.5
Еще одна проблема, связанная как с анализом сценариев, так и с имитационным анализом, состоит в том, что даже по завершении вычислительных процедур не


появляется четкого критерия принятия решения. Анализ завершается получением ожидаемого NPV и распределения значений вокруг него, которые можно использовать для оценки единичного риска проекта. Однако анализ не дает механизма, с помощью которого можно было бы четко определить, достаточна ли прибыльность проекта, мерой которой является его ожидаемый NPV, для компенсации его риска, показателем которого являются 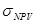 или CVNPV.
или CVNPV.
Наконец, поскольку анализ сценариев и имитационный анализ сосредоточены на единичном риске проекта, они игнорируют воздействие внутрифирменной диверсификации проектов, а также степени диверсифицированности персональных портфелей инвесторов. Таким образом, если отдельный проект оценивается изолированно, его доходы могут быть крайне неопределенными. Однако если эти доходы не коррелируют с доходами от других активов фирмы или с доходами от портфеля акций, тогда проект может быть не очень рисковым в смысле либо внутрифирменного, либо рыночного риска. Действительно, если доходы проекта отрицательно коррелируют с доходами от других активов Фирмы, тогда он может снизить корпорационный риск фирмы, и чем больше его 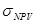 , тем больше он снизит общий риск фирмы. Аналогично, если доходность проекта не имеет положительной корреляции с фондовым рынком, тогда, возможно, даже проект с очень неустойчивыми доходами нельзя считать рисковым для хорошо диверсифицированных акционеров, которые обычно рыночным риском озабочены больше, чем единичным или внутрифирменным.
, тем больше он снизит общий риск фирмы. Аналогично, если доходность проекта не имеет положительной корреляции с фондовым рынком, тогда, возможно, даже проект с очень неустойчивыми доходами нельзя считать рисковым для хорошо диверсифицированных акционеров, которые обычно рыночным риском озабочены больше, чем единичным или внутрифирменным.

Анализ дерева решений
В предыдущих разделах внимание акцентировалось на методах оценки единичного риска проекта. Несмотря на то что такая оценка является неотъемлемой частью процесса формирования бюджета капиталовложений, менеджеры гораздо больше заинтересованы в уменьшении риска, а не в измерении его. Часто затраты на реализацию проекта не являются одномоментными, а осуществляются в течение периода, исчисляемого годами, что дает менеджерам возможность пересмотреть принятие решения и либо вложить в проект дополнительные денежные средства, либо прекратить (отвергнуть) проект. Проекты, структура которых позволяет делать капиталовложения в течение нескольких лет, часто оцениваются с использованием дерева решений.
Например предположим, что «Robotics International, Ltd.» рассматривает возможность производства промышленных роботов для отрасли промышленности, выпускающей телевизоры. Чистые инвестиции по этому проекту осуществляются в три этапа (рис. 9.4).
Этап 1. В момент t — 0, который в данном случае имеет место где-то в ближайшем будущем, проводится изучение (стоимостью в 500000 дол.) рыночного потенциала для применения роботов на линиях сборки телевизоров.
Этап 2. Если окажется, что значительный рынок для телевизионных сборочных роботов действительно существует, тогда в момент t = 1 расходуется 1 млн. дол. на разработку и изготовление нескольких опытных образцов роботов. Эти роботы затем оцениваются инженерами из телевизионной промышленности, и их мнения определяют, будет ли фирма продолжать работу над проектом.
Этап 3. Если опытные образцы роботов хорошо себя покажут, тогда в момент t = 2 в строительстве производственного предприятия инвестируется 10 млн. дол. Менеджеры прогнозируют, что чистый денежный поток, генерируемый в течение последующих четырех лет, может варьировать в зависимости от спроса на продукцию.
В данном случае считается, что между решениями проходит один год. Каждый кружок означает выбор того или иного решения. Сумма в долларах слева от момента принятия решения означает размер чистой инвестиции, необходимой в случае принятия этого решения, а денежные потоки, показанные под t 3—6, — это денежные поступления, возникающие в случае принятия проекта. Каждая диагональная линия представляет собой ветвь дерева решений, и каждая ветвь имеет рассчитанную вероятность. Например, если фирма решит начать работу над проектом, к моменту принятия решения 1 она должна будет потратить 500000 дол. на маркетинговое исследование. По оценке руководства, вероятность того, что исследование даст благоприятные результаты, составляет 0.8. Это приведет к решению перейти к этапу 2. Вероятность того, что маркетинговое исследование даст отрицательные результаты и укажет на то, что от проекта следует отказаться, составляет 0.2. Если работа по проекту прекратятся, расходы компании на начальное маркетинговое исследование в размере 500000 дол. будут списаны в убыток.
Если маркетинговое исследование предпринято и его результаты положительны, тогда «Robotics International» на следующем этапе потратит 1 млн. дол. на изго
|
|
|


