 |
Лекция 48. Понятие о степенных рядах. Интервал сходимости степенного ряда. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена. Примеры разложения функций в ряды.
|
|
|
|
Определение 1. Степенным рядом называется функциональный ряд вида
(1)
где а0,а1,а2,…, аn – постоянные числа, называемые коэффициентами ряда.
Ряд вида
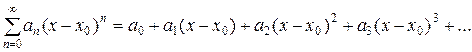(2)
также является степенным рядом. Это – степенной ряд, расположенный по степеням двучлена (x-a). Еще такой ряд называют обобщенным степенным рядом.
Начнем с того, что найдем область сходимости степенного ряда (1). Для этого проанализируем положительный числовой ряд, составленный из его модулей:
(3)
Применим к нему признак Даламбера. Для этого найдем q:
; (4)
Введем обозначение
, откуда 
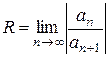(5)
Тогда выражение для q примет вид:
(6)
Согласно признака Даламбера:
1) Если q <1, то есть если | x | < R, или, что одно и то же, если – R < x < R, то ряд (3) сходится. А вместе с ним сходится, причем абсолютно, и ряд (1).
2) Если q >1, то есть | x|>R или, что одно и то же, если x > R или x < –R, то ряд (3) расходится. Заметим, что при этом и ряд (1) тоже не будет сходиться, ибо условие 
для любого положительного ряда 
означает, что начиная с некоторого номера N, то есть при n >N, отношение 
становится больше 1 и остается таковым для любых n >N. А это значит, что для n >N будет 
. То есть начиная с номера N члены 
положительного ряда растут, а значит, заведомо не стремятся к нулю. Получается нарушенным необходимое условие сходимости ряда 
, а заодно – и степенного ряда 
, ибо слагаемые первого из них – просто модули последнего. То есть действительно при x > R и x < –R ряд (1) будет расходиться.
3) Наконец, если q = 1, то есть если x = ± R, то о сходимости – расходимости и ряда (3), и ряда (1) ничего сказать нельзя. Этот случай нужно исследовать особо.
Итак, выводы:
Степенной ряд (1) сходится при –R < x < R; расходится при x > R и x < – R; при x = ± R он может как сходиться, так и расходиться (рис.1).
|
|
|
Величина R, определяемая по формуле (5), называется радиусом сходимости степенного ряда (1). А интервал (- R; R) называется интервалом сходимости этого степенного ряда. Областью сходимости D степенного ряда (1), таким образом, является его интервал сходимости (- R; R) и, возможно, его концы. Этот интервал, в частности, может вырождаться в точку.
Пример 1. Найти область сходимости степенного ряда 
.
Решение. Данный ряд – это ряд вида (1) при 
. Определим, используя формулу (5), его радиус сходимости R:
.
Итак, данный степенной ряд сходится при x є (- 2; 2) и, возможно, еще в точках x = ± 2. Для всех остальных x он расходится.
Исследуем ряд при x = ± 2.
1) Если x = 2, то наш ряд примет вид:
Это – гармонический ряд без первых двух своих членов. А значит, он расходится.
2) Если x = - 2, то получим:
Это – знакочередующийся ряд, сходящийся по признаку Лейбница.
Таким образом, областью сходимости D степенного ряда является полуинтервал [- 2; 2).
Степенные ряды (1) обладают замечательным свойством: внутри их интервалов сходимости (- R; R) их можно почленно дифференцировать и интегрировать. Это значит, что если
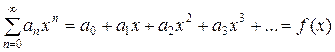, (- R < x < R) (7)
то
; (8)
. (9)
Эти факты примем без доказательства. Ограничимся лишь приведением примеров их использования.
Пример 2. Рассмотрим степенной ряд
(10)
Это – степенной ряд вида (1) при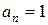 
(n = 0, 1, 2, …). Его радиус сходимости R, согласно формуле (5), равен 1: R = 1. То есть ряд (10) сходится в интервале (-1; 1), причем на обоих концах этого интервала он, очевидно, расходится. А так как этот ряд представляет собой еще и сумму бесконечной геометрической прогрессии со знаменателем x, то известна и его сумма:
(11)
Заменяя в (11) x на - x, получим еще один степенной ряд с известной суммой:
(12)
Если теперь почленно продифференцировать равенства (11) и (12), то получим еще два разложения:
(13)
(14)
А если равенство (12) почленно проинтегрировать в промежутке [0; t ], где 
, то получим:
|
|
|
(15)
Или в обычных обозначениях (заменив t на x):
(16)
Перейдя в этом равенстве к пределу при x ®1, получим:
(17)
Равенства (11) – (16) являются разложениями в степенные ряды, расположенные слева, тех функций, которые находятся справа.
Рассмотрим теперь общую проблему разложения любой заданной функции f(x) в степенной ряд (1). Для этого обратимся к формуле Маклорена:
(18)
Здесь
, 
(19)
- остаточный член формулы Маклорена, записанный в форме Лагранжа.
Допустим, что функция f(x) имеет при x = 0 производные любого порядка. И допустим, что для некоторого множества значений аргумента x 
при 
. Тогда переходя в формуле Маклорена (18) к пределу при , для этих значений x получим:
(20)
Формула (20) представляет собой не что иное, как разложение функции f(x) в степенной ряд. Этот ряд называется рядом Маклорена. Разложение (20) верно и может быть использовано лишь для тех x, для которых при 
.
Пример 3. Пусть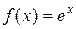 
. Тогда 
, а значит, 
. Разложение Маклорена (20) в данном случае примет вид:
(21)
Выясним теперь, для каких значений x оно справедливо. Для этого выпишем и проанализируем остаточный член 
. Так как 
при любом n, то
(22)
Покажем, что 
при 
для любого 
. Для этого рассмотрим положительный числовой ряд 
. Применим к нему признак Даламбера:
(23)
- при любом x. Значит, ряд 
сходится при любом x. Но тогда, в силу необходимого условия сходимости любого ряда, 
при . И это выполняется для любых x, 
. Значит, и разложение (21) справедливо для любых x:
(24)
Совершенно аналогично можно доказать и много других разложений различных функций в степенной ряд Маклорена. Например:
х – в радианах) (25)
х – в радианах) (26)
любое) (27)
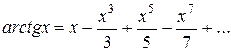
(28)
Разложения (24) – (28) и им подобные широко используются как для приближенного вычисления значений стоящих слева функций с любой заданной точностью, так и для различных математических операций с указанными функциями.
Пример 4. Вычислить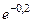 
с точностью до 0,0001.
Решение. Используя разложение (24) при х = - 0,2, получим:
Отбрасывая в получившемся знакочередующемся ряде четвертое слагаемое, меньшее допустимой погрешности 0,0001, и все последующие за ним, которые еще меньше, получим с требуемой точностью:
.
Пример 5. Вычислить приближенно с точностью до 0,001 неберущийся определенный интеграл 
.
|
|
|
Решение. Используя разложение (26), получим:
Отбрасывая в получившемся знакочередующемся числовом ряде четвертое слагаемое, которое меньше допустимой погрешности 0,001, и все последующие за ним, получим с требуемой точностью 0,001:
. (29)
Пример 6. Построить в виде степенного ряда приближенное решение задачи Коши
(30)
Эта задача, заметим, не имеет точного решения, так как дифференциальное уравнение 
не может быть решено в квадратурах.
Решение. Искомое решение 
ищем в виде ряда Маклорена:
(31)
Для неизвестных коэффициентов 
, 
, 
, 
… этого ряда получаем:
1) 
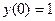- согласно начальному условию задачи Коши (30).
2) 
согласно обоим равенствам задачи Коши (30).
3) Дифференцируя обе части уравнения , получим: 
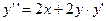. Полагая здесь х = 0 и учитывая, что 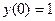и 
, получим: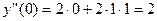 
;
4) Дифференцируя обе части равенства 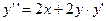, получим: 
, откуда 
.
Продолжая этот процесс, можем получить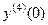 
; 
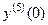, и т.д. В итоге на основании (31) искомое решение задачи Коши (30) примет вид:
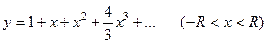(32)
На основании общей теории дифференциальных уравнений можно доказать, что ряд (32) сходится для всех 
. То есть его радиус сходимости 
. Ограничиваясь найденными первыми четырьмя слагаемыми этого ряда, получим следующее приближенное решение задачи Коши (30):
(33)
Оно будет тем точнее, чем ближе х к нулю.
|
|
|
