Интервалы монотонности функции.

Вопрос 58.

Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)
• аркко́синус (обозначение: arccos)
• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccotan)
• арксе́канс (обозначение: arcsec)
• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1

Производные обратных тригонометрических функций:

Вопрос 59.

Производная логарифмической функции для любого х из области определения находится по формуле

(1)

 

По основному логарифмическому тождеству х = е^{ln х} при всех положительных х, т. е. в этом равенстве справа и слева стоит одна и та же функция (определенная на R₊). Поэтому производные х и е^{ln x} равны, т. е.

x' = (e^{ln x})' (2)

 

Известно, что х' = 1. Производную правой части вычисляем по правилу нахождения производной сложной функции и теореме 1: (е^{ln x})'= е^{ln х} ln' x=x ln' x. Подставляя найденные производные в равенство (2), находим l = х ln' х, откуда .

Вопрос 60.

Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это функция, у которой и степень и основание зависят от «икс». Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле .

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера №11.

В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.

Логарифмическое дифференцирование

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.

Рассмотрим этот подход более детально. Пусть дана функция y = f (x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

Отсюда видно, что искомая производная равна

Вопрос 61.

ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

 

Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f'(x), вообще говоря, зависит от x, т.е. производная f'(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x).

Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'.

Например, если

 

у = х⁵, то y'= 5x⁴, а y''= 20x⁴.

 

Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x).

Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y⁽ⁿ⁾ или f⁽ⁿ⁾(x): y⁽ⁿ⁾ = (y^(n-1))'.

Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.

Вопрос 62. Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась дельтаХ, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания.

Вопрос 63.

Интервалы монотонности функции.

Функция возрастает.если её производная положительна,и убывает,если производная отрицательна.
1)F'(x)=2x+1
2x+1>0=>при x>-1/2 ф-я возрастает
при x<-1/2 ф-я убывает.
2)F'(x)=14x+14
14x+14>0=>при x>-1 ф-я возрастает
при x<-1 ф-я убывает.
3)F'(x)=2x^2-2
2x^2-2>0;(x-1)(x+1)>0;ф-я возрастает при x<-1 и x>1
при х от -1 до 1 ф-я убывает.
4)F'(x)=-1/(3x^2)
производная всегда,кроме 0,отрицательна,значит,ф-я убывает.

Экстремумы функции .

Решение. Данная функция определена для всех действительных чисел, ее производная имеет вид . При этом производная не определена там, где в нуль обращается знаменатель, т.е. при x=0. Эта точка является критической. Стационарных точек нет, так как в числителе стоит постоянное число, и потому дробь не обращается в нуль. Учитывая, что знак производной совпадает со знаком , а потому и со знаком x, получаем, что слева от x=0 (там, где x<0) , а справа . Поэтому x=0 – точка минимума исходной функции, и .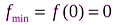

Вопрос 64.

Необходимый признак экстремума.

В точке экстремума производная функции либо

равна нулю, либо функция недифференцируема.

Но, разумеется, этот признак – не достаточный:

он не гарантирует того, что если в точке производная равна нулю или не существует, то эта точка будет точкой экстремума. На рисунке

f/(c)=0, но экстремума в точке x=c нет!

Условимся точки, в которых выполняется

необходимый признак экстремума называть

критическими точками функции.

Поделиться:

Воспользуйтесь поиском по сайту: